Bài 2: Hệ hai phương trình bậc nhất hai ẩn. Luyện tập

Lời giải:
$(d4)$ đi qua $A(-1;2)$ khi mà: 

$3ax_A+2by_A=5\Leftrightarrow 3a(-1)+2b.2=5$

$\Leftrightarrow -3a+4b=5(1)$

Mặt khác:

$(d'): 2x+3y=1\Rightarrow y=\frac{-2}{3}x+\frac{1}{3}$

Để $(d')\perp (d4)$ thì với $k$ là hsg của $(d4)$ thì:

$k.\frac{-2}{3}=-1\Leftrightarrow k=\frac{3}{2}$
$\Leftrightarrow \frac{-3a}{2b}=\frac{3}{2}$ (đk: $b\neq 0$)

$\Leftrightarrow a=-b(2)$

Từ $(1); (2)\Rightarrow b=\frac{5}{7}; a=\frac{-5}{7}$

\(\left\{{}\begin{matrix}2x-y=1\\x-2y=-1\end{matrix}\right.\)

Ta có:

\(D=-4+1=-3\ne0\)

\(D_x=-2-1=-3\ne0\)

\(D_y=-2-1=-3\ne0\)

Vậy Hệ phương trình đã cho có 1 nghiệm duy nhất.

A(2;-3) => x = 2; y = -3

Thay x = 2 và y = -3 ta có:

\(\left(m-1\right).2+\left(m+1\right).\left(-3\right)=2m+1\\ \Leftrightarrow2m-2-3m-3=2m+1\\ \Leftrightarrow-m-5=2m+1\\ \Leftrightarrow3m=6\\ \Leftrightarrow m=2\)

Vậy m = 2

(1): x+y=4

=>y=4-x

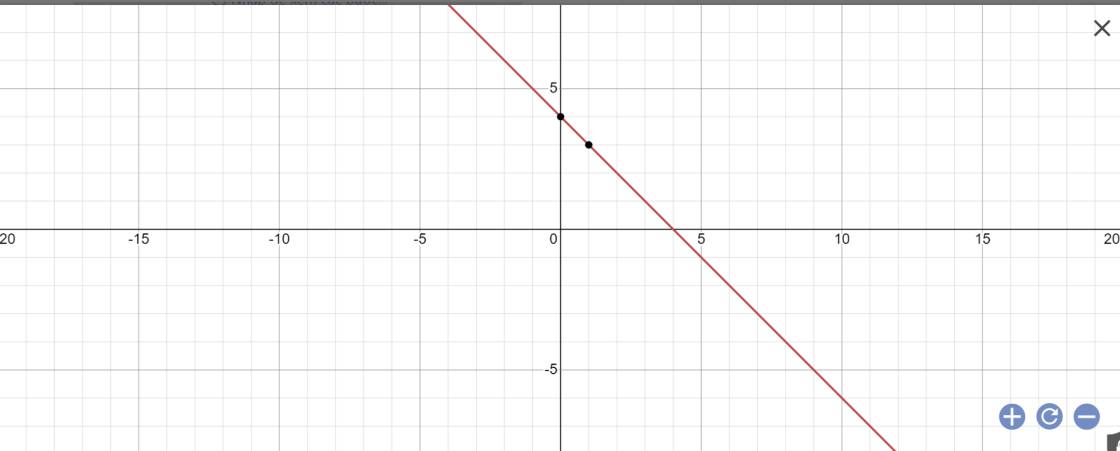
(2): 2x-y=-1

=>y=2x+1

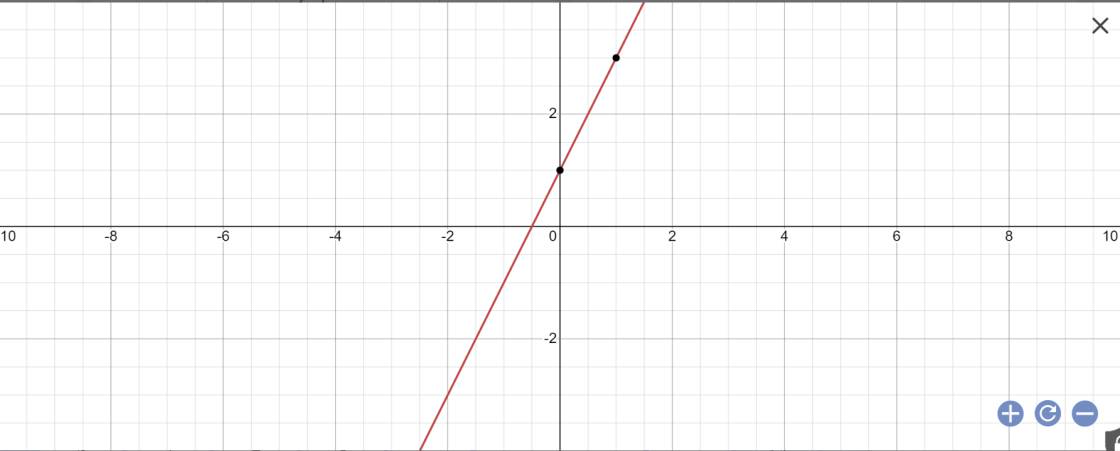
Bài 3:

\(\left\{{}\begin{matrix}x+y=3\\-mx-y=2m\end{matrix}\right.\left(1\right)\)

Ta có :

\(\left\{{}\begin{matrix}D=-1+m\\D_x=-3m-2m=-5m\\D_y=2m+3m=5m\end{matrix}\right.\)

Để (1) vô nghiệm \(\Leftrightarrow\left\{{}\begin{matrix}-1+m=0\\-5m\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m=1\\m\ne0\end{matrix}\right.\) \(\Leftrightarrow m=1\)

b) Để (1) có nghiệm duy nhất \(\Leftrightarrow-1+m\ne0\Leftrightarrow m\ne1\)

c) Để (1) có vô số nghiệm \(\Leftrightarrow\left\{{}\begin{matrix}-1+m=0\\-5m=0\\5m=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m=1\\m=0\\m=0\end{matrix}\right.\) \(\Leftrightarrow m\in\varnothing\)

a: Để hệ vô nghiệm thì \(\dfrac{1}{-m}=\dfrac{1}{-1}< >\dfrac{3}{2m}\)

=>m=1

b: Để hệ có nghiệm duy nhất thì 1/-m<>1/-1=-1

=>m<>1

c: Để hệ có vô số nghiệm thì \(\dfrac{1}{-m}=\dfrac{1}{-1}=\dfrac{3}{2m}\)

=>m=1 và 2m=-3

=>\(m\in\varnothing\)

a: Khi a=-2 thì ta sẽ có hệ phương trình: 3x-y=1 và -2x+2y=3

Vì 3/-2<>-1/2

nên hệ có nghiệm duy nhất

b: Khi a=-6 thì ta sẽ có hệ:

\(\left\{{}\begin{matrix}3x-y=1\\-6x+2y=3\end{matrix}\right.\)

Vì \(\dfrac{3}{-6}=\dfrac{-1}{2}< >\dfrac{1}{3}\)

nên hệ vô nghiệm

a: \(\left\{{}\begin{matrix}2x-3y=5\\4x+y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x-6y=10\\4x+y=3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}-7y=7\\4x+y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-1\\4x=3+1=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)

Thay x=1 và y=-1 vào hệ còn lại, ta được:

\(\left\{{}\begin{matrix}2\cdot1-3\cdot\left(-1\right)=5\\12\cdot1+3\cdot\left(-1\right)=a\end{matrix}\right.\Leftrightarrow a=12-3=9\)

b: \(\left\{{}\begin{matrix}x-y=2\\3x+y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x=3\\x-y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{4}\\y=\dfrac{3}{4}-2=-\dfrac{5}{4}\end{matrix}\right.\)

Thay x=3/4 và y=-5/4 vào hệ còn lại, ta được:

\(\left\{{}\begin{matrix}2\cdot a\cdot\dfrac{3}{4}-2\cdot\dfrac{-5}{4}=1\\\dfrac{3}{4}-\dfrac{5}{4}a=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{2}a=1+2\cdot\dfrac{-5}{4}=1-\dfrac{5}{2}=-\dfrac{3}{2}\\\dfrac{5}{4}a=\dfrac{3}{4}-2=-\dfrac{5}{4}\end{matrix}\right.\)

=>a=-1

\(\left\{{}\begin{matrix}x+y=7\\-x+2y=2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}-x-y=-7\\-x+2y=2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x+y=7\\\left[-x-\left(-x\right)\right]+\left(-y-2y\right)=-7-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+y=7\\-3y=-9\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x+y=7\\y=3\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x+3=7\\y=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=3\end{matrix}\right.\)

Vậy hệ pt có nghiệm duy nhất \(\left(x;y\right)=\left(4;3\right)\)