Câu 6. (3,0 điểm) Cho tam giác ABC nhọn nội tiếp (O), AB
DH
Những câu hỏi liên quan
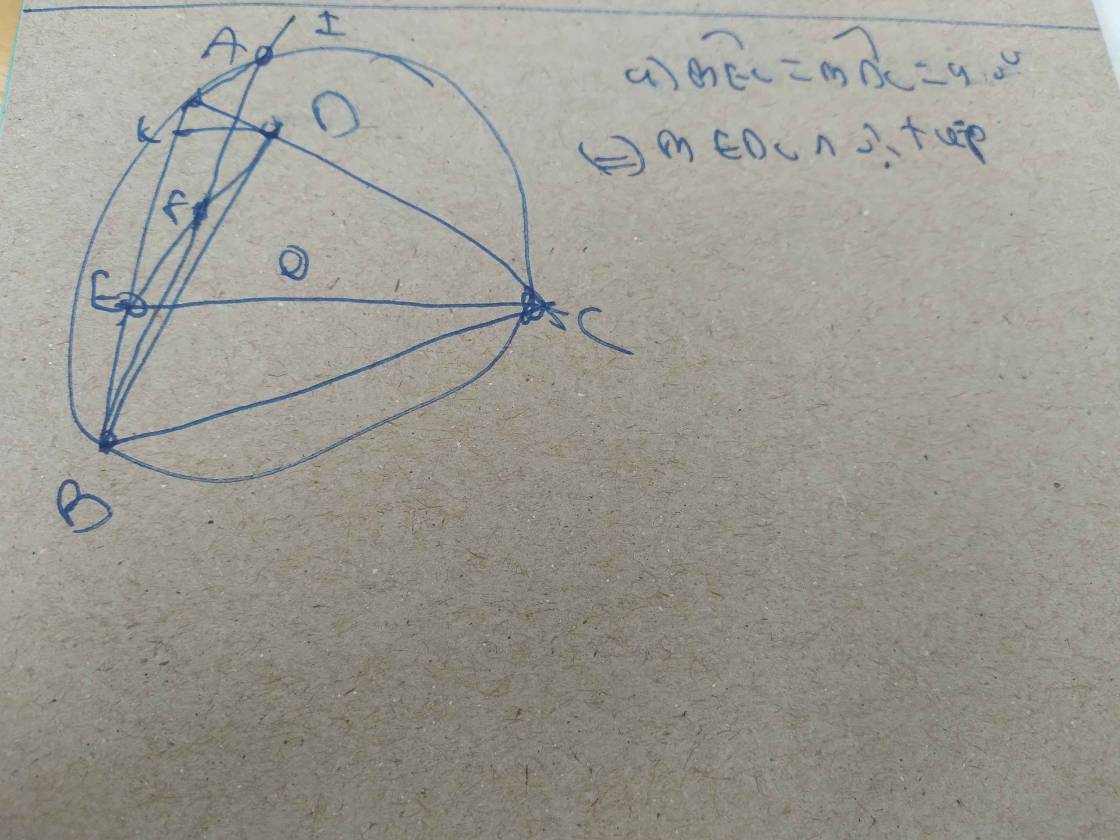
Câu 4. (3,0 điểm) Cho tam giác ABC nhọn nội tiếp (O), hai đường cao BD và CE của tam giác ABC cắt nhau tại H. Vẽ DK vuông góc với AB (K thuộc AB), gọi F là trung điểm của ED, tia BF cắt (O) tại I (khác B), a) Chứng minh tứ giác BEDC nội tiếp b) Chứng minh rằng BK.BA BF.BI c) Chứng minh rằng, hai đường thẳng AH và ID cắt nhau tại một điểm nằm trên (O).
Đọc tiếp
Câu 4. (3,0 điểm) Cho tam giác ABC nhọn nội tiếp (O), hai đường cao BD và CE của tam giác ABC cắt nhau tại H. Vẽ DK vuông góc với AB (K thuộc AB), gọi F là trung điểm của ED, tia BF cắt (O) tại I (khác B),
a) Chứng minh tứ giác BEDC nội tiếp
b) Chứng minh rằng BK.BA = BF.BI
c) Chứng minh rằng, hai đường thẳng AH và ID cắt nhau tại một điểm nằm trên (O).
AH cắt đường tròn tâm O tại M . Tam giác abd có dk là đường cao nên bk.ba=bd.bd mà bk.ba = bf.bi nên bd.bd =bf.bi
Nên bf/bd=bd/bi và góc ibd chung
Nên tam giác bfd đồng dạng tam giác bdi
Nên góc bdi = góc bid mà bdi=ecb=bcm
mà góc bia= góc bca
Cộng lại được aid=dcm
Aicm nội tiếp nên aim = dcm . Từ đó suy ra aid=aim
Nên i,d,m thẳng hàng nên ah và id cắt nhau tại điểm thuộc đường trón tâm o
Đúng 0
Bình luận (0)
Câu 5 (3,0 điểm). Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O. Các đường cao
AD, BE, CF của tam giác ABC cắt nhau tại H.
a) Chứng minh các tứ giác AEHF, BFEC nội tiếp đường tròn.
b) Đường thẳng AO cắt đường tròn tâm O tại điểm K khác điểm A. Gọi I là giao điểm của
hai đường thẳng HK và BC. Chứng minh I là trung điểm của đoạn thẳng BC.
c, tinh AH/AD + BH/BE + CH/CF 2
Đọc tiếp
Câu 5 (3,0 điểm). Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O. Các đường cao
AD, BE, CF của tam giác ABC cắt nhau tại H.
a) Chứng minh các tứ giác AEHF, BFEC nội tiếp đường tròn.
b) Đường thẳng AO cắt đường tròn tâm O tại điểm K khác điểm A. Gọi I là giao điểm của
hai đường thẳng HK và BC. Chứng minh I là trung điểm của đoạn thẳng BC.
c, tinh AH/AD + BH/BE + CH/CF =2
Câu 4(3,0 điểm) Cho tam giác ABC có ba góc nhọn (AB < AC), nội tiếp đường tròn tâm O. Các đường cao AD, BE, CF của tam giác ABC cắt nhau tại H. Gọi M là giao điểm của EF và BC. Qua B kẻ đường thẳng song song với AC cắt AM tại P và AD tại Q.
a) Chứng minh tứ giác AEHF nội tiếp.
b) Chứng minh DFC = EFC.
c) Chứng minh BP = BQ.
a: góc AEH+góc AFH=180 độ
=>AEHF nội tiếp
b: góc DFC=góc EBC
góc EFC=góc DAC
góc EBC=góc DAC
=>góc DFC=góc EFC
Đúng 0
Bình luận (0)
Bài IV. (3,0 điểm) Cho tam giác nhọn ABC (AB AC) nội tiếp đường tròn (O), các đường cao AD,BE cắt nhau tại H, F là chân đường vuông góc hạ từ B lên tiếp tuyến tại A của (O). Gọi K là trực tâm của tam giác BEF, đường thẳng CK cắt AF tại điểm M. 1) Chứng minh các điểm A, F, B, D, E cùng nằm trên một đường tròn .2) Chứng minh AMACAMACAFECAFEC và ABFCBE 3) Gọi N là chân đường cao hạ từ A lên BM . Chứng minh: BA là phân giác của MBC và N,K,E thẳng hàng.
Đọc tiếp
Bài IV. (3,0 điểm) Cho tam giác nhọn ABC (AB< AC) nội tiếp đường tròn (O), các đường cao AD,BE cắt nhau tại H, F là chân đường vuông góc hạ từ B lên tiếp tuyến tại A của (O). Gọi K là trực tâm của tam giác BEF, đường thẳng CK cắt AF tại điểm M.
1) Chứng minh các điểm A, F, B, D, E cùng nằm trên một đường tròn .
2) Chứng minh AMACAMAC=AFECAFEC và ABF=CBE
3) Gọi N là chân đường cao hạ từ A lên BM . Chứng minh: BA là phân giác của MBC và N,K,E thẳng hàng.
Bài IV. (3,0 điểm) Cho tam giác nhọn ABC (AB AC) nội tiếp đường tròn (O), các đường cao AD,BE cắt nhau tại H, F là chân đường vuông góc hạ từ B lên tiếp tuyến tại A của (O). Gọi K là trực tâm của tam giác BEF, đường thẳng CK cắt AF tại điểm M. 1) Chứng minh các điểm A, F, B, D, E cùng nằm trên một đường tròn .2) Chứng minh dfrac{AM}{AC}dfrac{AF}{EC} và ABFCBE 3) Gọi N là chân đường cao hạ từ A lên BM . Chứng minh: BA là phân giác của MBC và N,K,E thẳng hàng.
Đọc tiếp
Bài IV. (3,0 điểm) Cho tam giác nhọn ABC (AB< AC) nội tiếp đường tròn (O), các đường cao AD,BE cắt nhau tại H, F là chân đường vuông góc hạ từ B lên tiếp tuyến tại A của (O). Gọi K là trực tâm của tam giác BEF, đường thẳng CK cắt AF tại điểm M.
1) Chứng minh các điểm A, F, B, D, E cùng nằm trên một đường tròn .
2) Chứng minh \(\dfrac{AM}{AC}\)=\(\dfrac{AF}{EC}\) và ABF=CBE
3) Gọi N là chân đường cao hạ từ A lên BM . Chứng minh: BA là phân giác của MBC và N,K,E thẳng hàng.
1: góc AFB=góc AEB=góc ADB=90 độ
=>A,F,B,E,D cùng nằm trên 1 đường tròn
2: Xét ΔAFE và ΔACM có
góc FAE chung
góc AFE=góc ABE=góc ADE=góc MCA
=>ΔAFE đồng dạng với ΔACM
=>AE/AM=AF/AC
=>AM/AC=AE/AF
góc FAB=góc ACB
=>góc FBA=90 độ-góc ACB=góc EBC
Đúng 0
Bình luận (0)
Bài 5: (3,0 điểm). Cho tam giác ABC nhọn nội tiếp đừng tròn tâm O. Các đường cao AD, BE và CF cắt
nhau tại H. Đường thẳng EF cắt đường tròn ở I và K. Chứng minh:
a) Tứ giác BCEF nội tiếp.
b) AE.AC = AF.AB.
c) AI = AK.
câu C the nao ạ? cám ơn mọi nguoi
a Xét tứ giác BCEF có
\(\widehat{BFC}=\widehat{BEC}=90^0\)
Do đó:BCEF là tứ giác nội tiếp
b: Xét ΔABE vuông tại E và ΔACF vuông tại F có
\(\widehat{BAE}\) chung
DO đó: ΔABE\(\sim\)ΔACF
Suy ra: AB/AC=AE/AF
hay \(AB\cdot AF=AE\cdot AC\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có ba góc nhọn và ABAC. Tam giác ABC nội tiếp đường tròn (O;R). Đường cao AH của tam giác ABC cắt đường tròn (O;R) tại điểm thứ hai là D. Kẻ DM vuông góc với AB tại M.a) Chứng minh tứ giác BDHM nội tiếp đường tròn.b) Chứng minh DA là tia phân giác của widehat{MDC}c) Gọi N là hình chiếu vuông góc của D lên đường thẳng AC, chứng minh ba điểm M, H, N thẳng hàng.d) Chứng minh AB^2+AC^2+CD^2+BD^28R^2
Đọc tiếp
Cho tam giác ABC có ba góc nhọn và AB>AC. Tam giác ABC nội tiếp đường tròn (O;R). Đường cao AH của tam giác ABC cắt đường tròn (O;R) tại điểm thứ hai là D. Kẻ DM vuông góc với AB tại M.
a) Chứng minh tứ giác BDHM nội tiếp đường tròn.
b) Chứng minh DA là tia phân giác của \(\widehat{MDC}\)
c) Gọi N là hình chiếu vuông góc của D lên đường thẳng AC, chứng minh ba điểm M, H, N thẳng hàng.
d) Chứng minh \(AB^2+AC^2+CD^2+BD^2=8R^2\)
a: góc BHD+góc BMD=180 độ
=>BHDM nội tiếp
b: BHDM nội tiếp
=>góc HDM+góc HBM=180 độ
=>góc ADM=góc ABC
=>góc ADM=góc ADC
=>DA là phân giáccủa góc MDC
c: Xét tứ giác DHNC có
góc DHC=góc DNC=90 độ
=>DHNC nội tiếp
=>góc NHD=góc NDC
góc NHD+góc MHD
=180 độ-góc NCD+góc MBD
=180 độ+180 độ-góc ABD-góc ACD
=180 độ
=>M,H,N thẳng hàng
Đúng 0
Bình luận (0)
Câu III ( 3 điểm). Cho tam giác ABC nhọn nội tiếp đường tròn (O). Tiếp tuyến qua B,C của (O) cắt nhau tại T. Đường thẳng qua T song song với OA cắt trung trực CA, AB lần lượt tại các điểm E,F1) Chứng minh rằng hai tam giác OEF và ABC đồng dạng2) Gọi J là tâm đường tròn ngoại tiếp tam giác OEF. Chứng minh rằng: OJ//BC 3) Gọi K là trực tâm tam giác OEF. CMR: AT chia đôi đoạn thẳng OK
Đọc tiếp
Câu III ( 3 điểm). Cho tam giác ABC nhọn nội tiếp đường tròn (O). Tiếp tuyến qua B,C của (O) cắt nhau tại T. Đường thẳng qua T song song với OA cắt trung trực CA, AB lần lượt tại các điểm E,F
1) Chứng minh rằng hai tam giác OEF và ABC đồng dạng
2) Gọi J là tâm đường tròn ngoại tiếp tam giác OEF. Chứng minh rằng: OJ//BC
3) Gọi K là trực tâm tam giác OEF. CMR: AT chia đôi đoạn thẳng OK
giúp tôi câu c mọi người ơibài 1 cho tam giác ABC nhọn nội tiếp (O,R). hạ các đường cao AH và BK của tam giác. các tia AH và BK lần lượt cắt O tại điểm thứ hai là D và E.a. chứng minh tứ giác ABHK nội tiếp. tìm tâm của đường tròn đób.chứng minh rằng HK song song với DE.c. cho (O) và dây AB cố định, điểm C di động trên (O) sao cho tam giác ABC nhọn. CMR độ dài bán kính đương tròn ngoại tiếp tam giác CHK không đổi.
Đọc tiếp
giúp tôi câu c mọi người ơi
bài 1 cho tam giác ABC nhọn nội tiếp (O,R). hạ các đường cao AH và BK của tam giác. các tia AH và BK lần lượt cắt O tại điểm thứ hai là D và E.
a. chứng minh tứ giác ABHK nội tiếp. tìm tâm của đường tròn đó
b.chứng minh rằng HK song song với DE.
c. cho (O) và dây AB cố định, điểm C di động trên (O) sao cho tam giác ABC nhọn. CMR độ dài bán kính đương tròn ngoại tiếp tam giác CHK không đổi.
cho tam giác ABC nhọn có ABAC nội tiếp đường tròn tâm O , bán kính R . gọi H là giao điểm của 3 đường cao AD,BE,CF của tam giác ABC . kẻ đường kính AK của đường tròn (O) , AD cắt (O) tại điểm N1. chứng minh AEDB , AEHF là tứ giác nội tiếp và AB.AC2R.AD2. chứng minh HK đi qua tring điểm M của BC3. gọi bán kính đường tròn ngoại tiếp tứ giác AEHF là r . chứng minh OM^2R^2-r^24. chứng minh OC vuông góc với DE và N đối xứng với H qua đường thẳng BC
Đọc tiếp
cho tam giác ABC nhọn có AB<AC nội tiếp đường tròn tâm O , bán kính R . gọi H là giao điểm của 3 đường cao AD,BE,CF của tam giác ABC . kẻ đường kính AK của đường tròn (O) , AD cắt (O) tại điểm N
1. chứng minh AEDB , AEHF là tứ giác nội tiếp và AB.AC=2R.AD
2. chứng minh HK đi qua tring điểm M của BC
3. gọi bán kính đường tròn ngoại tiếp tứ giác AEHF là r . chứng minh OM^2=R^2-r^2
4. chứng minh OC vuông góc với DE và N đối xứng với H qua đường thẳng BC