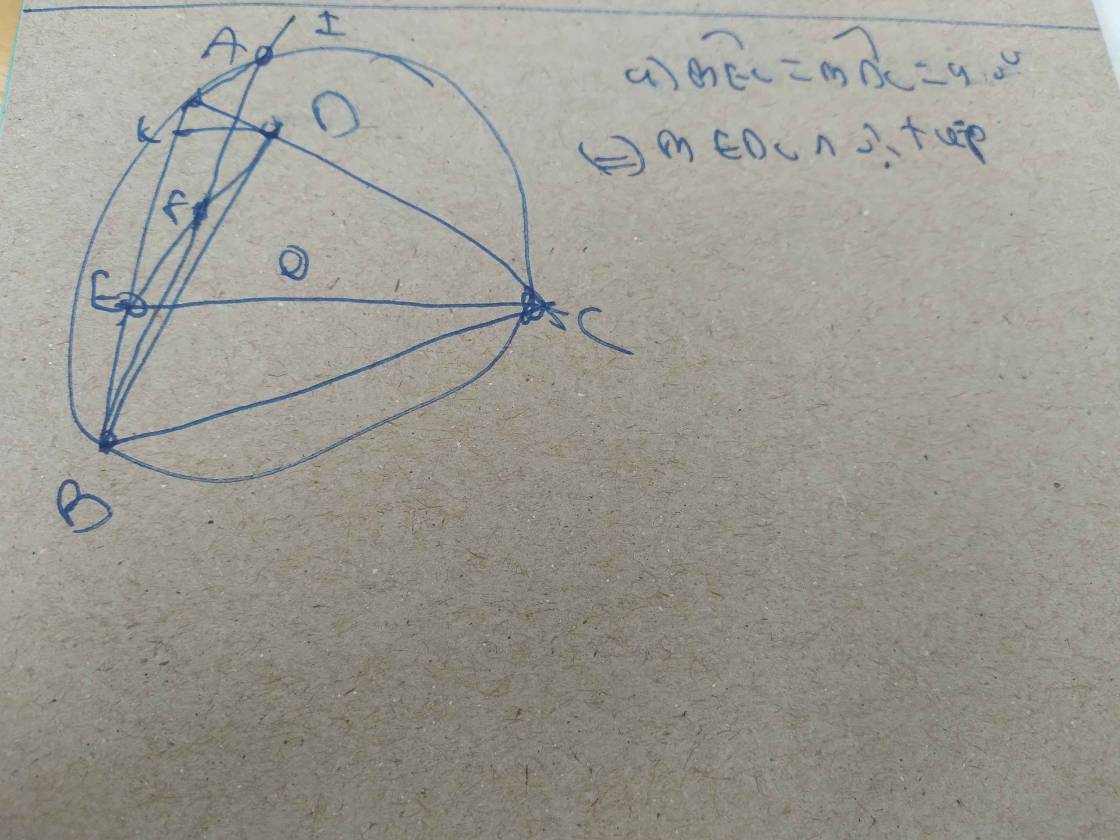
Câu 4. (3,0 điểm) Cho tam giác ABC nhọn nội tiếp (O), hai đường cao BD và CE của tam giác ABC cắt nhau tại H. Vẽ DK vuông góc với AB (K thuộc AB), gọi F là trung điểm của ED, tia BF cắt (O) tại I (khác B),
a) Chứng minh tứ giác BEDC nội tiếp
b) Chứng minh rằng BK.BA = BF.BI
c) Chứng minh rằng, hai đường thẳng AH và ID cắt nhau tại một điểm nằm trên (O).
AH cắt đường tròn tâm O tại M . Tam giác abd có dk là đường cao nên bk.ba=bd.bd mà bk.ba = bf.bi nên bd.bd =bf.bi
Nên bf/bd=bd/bi và góc ibd chung
Nên tam giác bfd đồng dạng tam giác bdi
Nên góc bdi = góc bid mà bdi=ecb=bcm
mà góc bia= góc bca
Cộng lại được aid=dcm
Aicm nội tiếp nên aim = dcm . Từ đó suy ra aid=aim
Nên i,d,m thẳng hàng nên ah và id cắt nhau tại điểm thuộc đường trón tâm o