Để tam thức bậc hai \({x^2} + (m + 1)x + 2m + 3 > 0\)với mọi \(x \in \mathbb{R}\)

Ta có: a = 1 >0 nên \(\Delta  < 0\)

\(\begin{array}{l} \Leftrightarrow {(m + 1)^2} - 4.(2m + 3) < 0\\ \Leftrightarrow {m^2} + 2m + 1 - 8m - 12 < 0\\ \Leftrightarrow {m^2} - 6m - 11 < 0\end{array}\)

Tam thức \(f(m) = {m^2} - 6m - 11\) có \(\Delta ' = 20 > 0\) nên f(x) có 2 nghiệm phân biệt \({m_1} =  3+\sqrt{20}; {m_2} = 3-\sqrt{20}\)

Khi đó 

\(  3+\sqrt{20} < m < 3-\sqrt{20}\)

Vậy \(  3+\sqrt{20} < m < 3-\sqrt{20}\)

f(x)>0 <=>\(x^2-\left(m+2\right)x+2m+1>0\)

Bất phương trình có a=1>0

=>Bất phương trình đúng với mọi x thuộc tập số thực

<=>\(\Delta< 0\)(Vì khi \(\Delta\)<0 thì f(x) cùng dấu a với mọi x thuộc tập số thực)

\(\Leftrightarrow\left(m-2\right)^2-4\left(2m+1\right)< 0\)

\(\Leftrightarrow m^2-12m< 0\)

\(\Leftrightarrow0< m< 12\)

Lời giải:

Áp dụng định lý về dấu của tam thức bậc 2

\(f(x)=3x^2-6(2m+1)x+12m+5>0\) với mọi \(x\in \mathbb{R}\)

\(\Leftrightarrow \Delta'=9(2m+1)^2-3(12m+5)<0\)

\(\Leftrightarrow 36m^2-6<0\Leftrightarrow -\sqrt{\frac{1}{6}}< m<\sqrt{\frac{1}{6}}\)

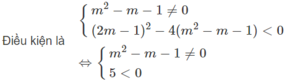
 Không có giá trị nào của m thỏa mãn điều kiện này.

Lời giải:

Áp dụng định lý về dấu của tam thức bậc 2.

a)

Để hàm \(f(x)=4x^2-(m+2)x+2m-3>0\forall x\in\mathbb{R}\)

\(\Leftrightarrow \Delta=(m+2)^2-16(2m-3)<0\)

\(\Leftrightarrow m^2-28m+52=(m-2)(m-26)<0\)

\(\Leftrightarrow 2< m<26\)

b)

Nếu \(m=-1\rightarrow f(x)=-6x\) không thể âm với mọi $x$

Nếu \(m\neq -1\):

Để \(f(x)=(m+1)x^2+2(2m-1)x-m-1<0\forall x\in\mathbb{R}\) thì cần hai đk sau:

1. \(m+1<0\leftrightarrow m<-1\)

2. \(\Delta'=(2m-1)^2+(m+1)^2<0\) (hiển nhiên vô lý)

Vậy không tồn tại $m$ thỏa mãn.

\(\Delta'=\left(m+5\right)^2-10m-24=m^2+1>0;\forall m\)

\(\Rightarrow f\left(x\right)=0\) luôn có 2 nghiệm pb với mọi m và: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m+5\right)\\x_1x_2=10m+24\end{matrix}\right.\)

Để \(f\left(x\right)>0;\forall x>2\)

\(\Leftrightarrow x_1< x_2< 2\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left(x_1-2\right)\left(x_2-2\right)>0\\\dfrac{x_1+x_2}{2}< 2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x_1x_2-2\left(x_1+x_2\right)+4>0\\x_1+x_2< 4\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}10m+24-4\left(m+5\right)+4>0\\2\left(m+5\right)< 4\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m>-\dfrac{4}{3}\\m< -3\end{matrix}\right.\) \(\Rightarrow\) không tồn tại m thỏa mãn