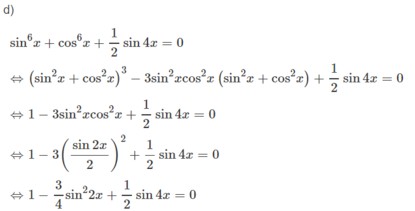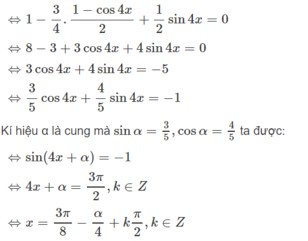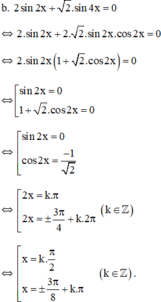
Vậy phương trình có tập nghiệm 

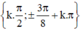 (k ∈ Z)

\(\Leftrightarrow2sin^3x+1-sin^2x-1=0\)

\(\Leftrightarrow sin^2x\left(2sinx-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\sinx=\dfrac{1}{2}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)

lm trên symbolab.com

\(\left(2\sin x-1\right)\left(2\sin2x+1\right)=3-4\cos^2x\)

\(\Leftrightarrow\left(2\sin x-1\right)\left(2\sin2x+1\right)=3-4\left(2-\sin^2x\right)\)

\(\Leftrightarrow\left(2\sin x-1\right)\left(2\sin2x+1\right)=4\sin^2x-1\)

\(\Leftrightarrow\left(2\sin x-1\right)\left(2\sin2x+1\right)=\left(2\sin x-1\right)\left(2\sin x+1\right)\)

\(\Leftrightarrow2\sin2x+1=2\sin x+1\)

\(\Leftrightarrow\sin2x=\sin x\)

\(\Leftrightarrow\sin2x-\sin x=0\)

\(\Leftrightarrow2\cos\frac{3}{2}-\cos\frac{x}{2}=0\)

\(\Leftrightarrow\orbr{\begin{cases}\cos\frac{3}{2}=0\\\cos\frac{x}{2}=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}\frac{3x}{2}=\frac{\pi}{2}+k2\pi\\\frac{x}{2}=\frac{\pi}{2}+k2\pi\end{cases}\left(k\inℤ\right)}\)

\(\Leftrightarrow\orbr{\begin{cases}x=\frac{\pi}{3}+\frac{2\pi}{3}k\\x=\pi+4k\pi\end{cases}\left(k\inℤ\right)}\)

Pt \(\Leftrightarrow sin\left(2x-\dfrac{\pi}{4}\right)=-\dfrac{\sqrt{3}}{2}\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-\dfrac{\pi}{4}=-\dfrac{\pi}{3}+k2\pi\\2x-\dfrac{\pi}{4}=\dfrac{4\pi}{3}+k2\pi\end{matrix}\right.\),\(k\in Z\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{24}+k\pi\\x=\dfrac{19\pi}{24}+k\pi\end{matrix}\right.\)\(\left(k\in Z\right)\)

Vậy...
Hôm qua họ bảo toi ra lấy CCCD nma toi chưa đi, nay toi đi họ lại đang họp, liệu mai toi đi có bị ăn chửi ko, mn cho ý kiến đi :<

\(2sin\left(2x-\dfrac{\pi}{4}\right)+\sqrt{3}=0\)

\(\Leftrightarrow sin\left(2x-\dfrac{\pi}{4}\right)=-\dfrac{\sqrt{3}}{2}\)

\(\Leftrightarrow sin\left(2x-\dfrac{\pi}{4}\right)=sin\left(-\dfrac{\pi}{3}\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-\dfrac{\pi}{4}=-\dfrac{\pi}{3}+k2\pi\\2x-\dfrac{\pi}{4}=\pi+\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}2x=-\dfrac{\pi}{12}+k2\pi\\2x=\dfrac{19\pi}{12}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{24}+k\pi\\x=\dfrac{19\pi}{24}+k\pi\end{matrix}\right.\)

b) \(2sin^2x-3sinxcosx+cos^2x=0\)

\(\Leftrightarrow2tan^2x-3tanx+1=0\left(cosx\ne0\Leftrightarrow x\ne\dfrac{\pi}{2}+k\pi\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}tanx=1\\tanx=\dfrac{1}{2}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}tanx=tan\dfrac{\pi}{4}\\tanx=\dfrac{1}{2}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=arctan\left(\dfrac{1}{2}\right)+k\pi\end{matrix}\right.\left(k\in Z\right)\)

ĐK: \(x\ne\dfrac{\pi}{4}+k\pi;x\ne\dfrac{k\pi}{2}\)

\(\dfrac{2sin^2x+cos4x-cos2x}{\left(sinx-cosx\right)sin2x}=0\)

\(\Leftrightarrow2sin^2x+cos4x-cos2x=0\)

\(\Leftrightarrow2sin^2x-1+cos4x-cos2x+1=0\)

\(\Leftrightarrow2cos^22x-2cos2x=0\)

\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\\cos2x=1\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{2}+k\pi\\2x=k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\\x=k\pi\end{matrix}\right.\)

Đối chiếu điều kiện ta được \(x=-\dfrac{\pi}{4}+k\pi\)

a: \(2\cdot sin\left(x+\dfrac{\Omega}{5}\right)+\sqrt{3}=0\)

=>\(2\cdot sin\left(x+\dfrac{\Omega}{5}\right)=-\sqrt{3}\)

=>\(sin\left(x+\dfrac{\Omega}{5}\right)=-\dfrac{\sqrt{3}}{2}\)

=>\(\left[{}\begin{matrix}x+\dfrac{\Omega}{5}=-\dfrac{\Omega}{3}+k2\Omega\\x+\dfrac{\Omega}{5}=\dfrac{4}{3}\Omega+k2\Omega\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}x=-\dfrac{8}{15}\Omega+k2\Omega\\x=\dfrac{4}{3}\Omega-\dfrac{\Omega}{5}+k2\Omega=\dfrac{17}{15}\Omega+k2\Omega\end{matrix}\right.\)

b: \(sin\left(2x-50^0\right)=\dfrac{\sqrt{3}}{2}\)

=>\(\left[{}\begin{matrix}2x-50^0=60^0+k\cdot360^0\\2x-50^0=300^0+k\cdot360^0\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}2x=110^0+k\cdot360^0\\2x=350^0+k\cdot360^0\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}x=55^0+k\cdot180^0\\x=175^0+k\cdot180^0\end{matrix}\right.\)

c: \(\sqrt{3}\cdot tan\left(2x-\dfrac{\Omega}{3}\right)-1=0\)

=>\(\sqrt{3}\cdot tan\left(2x-\dfrac{\Omega}{3}\right)=1\)

=>\(tan\left(2x-\dfrac{\Omega}{3}\right)=\dfrac{1}{\sqrt{3}}\)

=>\(2x-\dfrac{\Omega}{3}=\dfrac{\Omega}{6}+k2\Omega\)

=>\(2x=\dfrac{1}{2}\Omega+k2\Omega\)

=>\(x=\dfrac{1}{4}\Omega+k\Omega\)