 cho em xin bài giải ạ :<
cho em xin bài giải ạ :<
H24
Những câu hỏi liên quan
cho em xin giải chi tiết của bài này ạ, em xin cảm ơn rất nhiều TT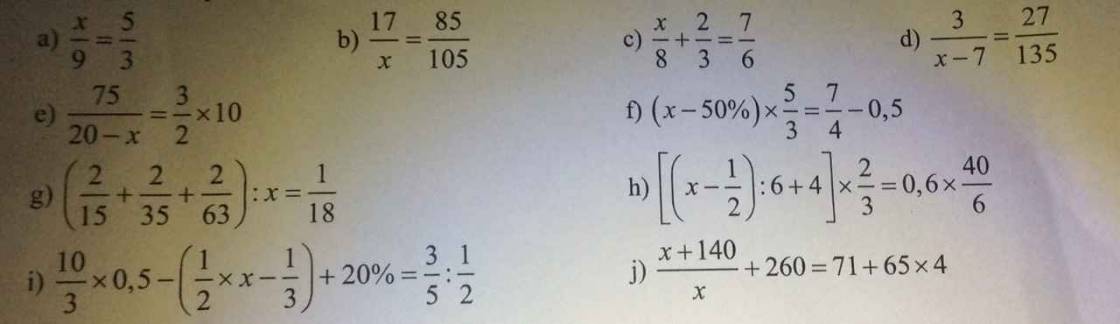
\(a,\dfrac{x}{9}=\dfrac{5}{3}\\ \Leftrightarrow x=9\cdot\dfrac{5}{3}\\ \Leftrightarrow x=15\\ b,\dfrac{17}{x}=\dfrac{85}{105}\\ \Leftrightarrow x=17\cdot\dfrac{105}{85}\\ \Leftrightarrow x=21\\ c,\dfrac{x}{8}+\dfrac{2}{3}=\dfrac{7}{6}\\ \Leftrightarrow\dfrac{x}{8}=\dfrac{1}{2}\\ \Leftrightarrow x=4\\ d,\dfrac{3}{x-7}=\dfrac{27}{135}\\ \Leftrightarrow x-7=15\\ \Leftrightarrow x=22\)
Đúng 0
Bình luận (0)
\(e,\dfrac{75}{20-x}=\dfrac{3}{2}\times10\\ \Leftrightarrow\dfrac{75}{20-x}=15\\ \Leftrightarrow20-x=5\\ \Leftrightarrow x=15\\ f,\left(x-50\%\right)\times\dfrac{5}{3}=\dfrac{7}{4}-0,5\\ \Leftrightarrow\left(x-\dfrac{1}{2}\right)\times\dfrac{5}{3}=\dfrac{5}{4}\\ \Leftrightarrow x-\dfrac{1}{2}=\dfrac{3}{4}\\ \Leftrightarrow x=\dfrac{5}{4}\\ g,\left(\dfrac{2}{15}+\dfrac{3}{35}+\dfrac{2}{63}\right):x=\dfrac{1}{18}\\ \Leftrightarrow\dfrac{2}{9}:x=\dfrac{1}{18}\\ \Leftrightarrow x=4\)
\(h,\left[\left(x-\dfrac{1}{2}\right):6+4\right]\times\dfrac{2}{3}=0,6\times\dfrac{40}{6}\\ \Leftrightarrow\left[\left(x-\dfrac{1}{2}\right):6+4\right]\times\dfrac{2}{3}=4\\ \Leftrightarrow\left(x-\dfrac{1}{2}\right):6+4=6\\ \Leftrightarrow\left(x-\dfrac{1}{2}\right):6=2\\ \Leftrightarrow x-\dfrac{1}{2}=12\\ \Leftrightarrow x=\dfrac{25}{2}\)
Đúng 0
Bình luận (0)
\(i,\dfrac{10}{3}\times0,5-\left(\dfrac{1}{2}\times x-\dfrac{1}{3}\right)+20\%=\dfrac{3}{5}:\dfrac{1}{2}\\ \Leftrightarrow\dfrac{5}{3}-\dfrac{1}{2}x+\dfrac{1}{3}+\dfrac{1}{5}=\dfrac{6}{5}\\ \Leftrightarrow\dfrac{1}{2}x=1\\ \Leftrightarrow x=2\)
\(j,\dfrac{x+140}{x}+260=71+65\times4\\ \Leftrightarrow\dfrac{x+140}{x}=71\\ \Leftrightarrow x+140=71x\\ \Leftrightarrow70x=140\\ \Leftrightarrow x=2\)
Đúng 1
Bình luận (0)
Mn cho em xin lời giải bài này ạ..... Em cảm ơn mn nhiều ạ

\(y'=-3mx^2+2x-3\)
Hàm nghịch biến trên khoảng đã cho khi với mọi \(x\in\left(-3;0\right)\) ta có:
\(-3mx^2+2x-3\le0\)
\(\Leftrightarrow2x-3\le3mx^2\)
\(\Leftrightarrow\dfrac{2x-3}{3x^2}\le m\)
\(\Rightarrow m\ge\max\limits_{\left(-3;0\right)}\left(\dfrac{2x-3}{3x^2}\right)\)
Xét hàm \(f\left(x\right)=\dfrac{2x-3}{3x^2}\Rightarrow f'\left(x\right)=\dfrac{2\left(3-x\right)}{3x^3}< 0;\forall x\in\left(-3;0\right)\)
\(\Rightarrow f\left(x\right)>f\left(-3\right)=-\dfrac{1}{3}\)
\(\Rightarrow m\ge-\dfrac{1}{3}\)
Đúng 1
Bình luận (0)
Giúp em bài này với, cho em xin thêm bài giải nhé ạ. Em thanks trước nhé

Nhanh hộ em với 3h em phải nộp bài ạ
Đúng 1
Bình luận (0)
ai làm nhanh hộ em, em sẽ like trong 1- 10 ngày ạ. ![]()
Đúng 1
Bình luận (0)
\(\dfrac{0,25.140.154.0,1.121.5:100}{140:4.154:1012,1:0,01}\)
=\(\dfrac{140:4.154 :10.121,5:0,01}{140:4.154:10.121,5:0,01}\)
=1
Đúng 0
Bình luận (1)
Cho em xin lời giải bài này ạ!!! Em cảm ơn ![]()
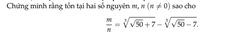
Đặt \(x=\sqrt[3]{\sqrt[]{50}+7}-\sqrt[3]{\sqrt[]{50}-7}\)
\(x^3=14-3\sqrt[3]{\left(\sqrt[]{50}+7\right)\left(\sqrt[]{50}-7\right)}\left(\sqrt[3]{\sqrt[]{50}+7}-\sqrt[3]{\sqrt[]{50}-7}\right)\)
\(x^3=14-3x\)
\(x^3+3x-14=0\)
\(\left(x-2\right)\left(x^2+2x+7\right)=0\)
\(x=2\)
\(\Rightarrow\dfrac{m}{n}=2\)
\(\Rightarrow\) Hiển nhiên tồn tại vô số m, n nguyên thỏa mãn đẳng thức trên
Đúng 0
Bình luận (0)
Cho em xin bài giải đầy đủ ạ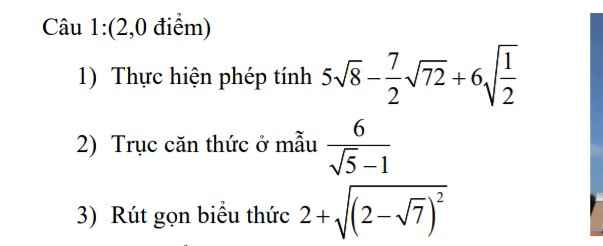
\(1,=10\sqrt{2}-21\sqrt{2}+3\sqrt{2}=-8\sqrt{2}\\ 2,=\dfrac{6\left(\sqrt{5}+1\right)}{4}=\dfrac{3\sqrt{5}+3}{2}\\ 3,=2+\left|2-\sqrt{7}\right|=2+\sqrt{7}-2=\sqrt{7}\)
Đúng 0
Bình luận (0)
Cho em xin bài giải đầy đủ ạ
cho em xin bài giải chi tiết ạ
a: Xét tứ giác ABEC có
D là trung điểm của AE
D là trung điểm của BC
Do đó: ABEC là hình bình hành
Suy ra:AB//CE
Đúng 1
Bình luận (0)
Cho em xin lời giải bài 3 và bài 4 với ạ
Chỉ thấy bài 5 với 6:
5.
\(f'\left(x\right)+2f\left(x\right)=0\Leftrightarrow f'\left(x\right)=-2f\left(x\right)\Leftrightarrow\dfrac{f'\left(x\right)}{f\left(x\right)}=-2\)
Lấy nguyên hàm 2 vế:
\(\int\dfrac{f'\left(x\right)}{f\left(x\right)}dx=\int-2dx\Rightarrow ln\left(f\left(x\right)\right)=-2x+C\)
Thay \(x=1\Rightarrow0=-2+C\Rightarrow C=2\)
\(\Rightarrow ln\left(f\left(x\right)\right)=-2x+2\Rightarrow f\left(x\right)=e^{-2x+2}\)
\(\Rightarrow f\left(-1\right)=e^4\)
Đúng 4
Bình luận (0)
6.
\(f\left(x\right)+x.f'\left(x\right)=2x+1\)
\(\Leftrightarrow x'.f\left(x\right)+x.f'\left(x\right)=2x+1\)
\(\Leftrightarrow\left[x.f\left(x\right)\right]'=2x+1\)
Lấy nguyên hàm 2 vế:
\(\int\left[x.f\left(x\right)\right]'dx=\int\left(2x+1\right)dx\)
\(\Rightarrow x.f\left(x\right)=x^2+x+C\)
Thay \(x=1\Rightarrow1.f\left(1\right)=1+1+C\Rightarrow C=1\)
\(\Rightarrow f\left(x\right)=\dfrac{x^2+x+1}{x}\)
\(\Rightarrow f\left(2\right)=\dfrac{7}{2}\)
Đúng 1
Bình luận (0)
Ủa sao đề khác rồi:
3.
\(f'\left(x\right)=-e^x.f^2\left(x\right)\Leftrightarrow\dfrac{f'\left(x\right)}{f^2\left(x\right)}=-e^x\)
Lấy nguyên hàm 2 vế:
\(\int\dfrac{f'\left(x\right)}{f^2\left(x\right)}dx=\int-e^xdx\)
\(\Rightarrow\dfrac{1}{f\left(x\right)}=e^x+C\)
Thay \(x=0\Rightarrow2=1+C\Rightarrow C=1\)
\(\Rightarrow\dfrac{1}{f\left(x\right)}=e^x+1\Rightarrow f\left(x\right)=\dfrac{1}{e^x+1}\)
\(\Rightarrow f\left(ln2\right)=\dfrac{1}{3}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
 cho em xin cách giải và đáp án bài này với ạ
cho em xin cách giải và đáp án bài này với ạ
#include <bits/stdc++.h>
using namespace std;
int main (){
int n;
cin >> n;
int a[n];
long long t=0,k=0;
for (int i=1;i<=n;i++) cin >> a[i];
for (int i=1;i<=n;i++) {
int lt=1;
for (int j=1;j<=i;j++)
lt=lt*a[i];
t=t+lt;
}
cout << t;
return 0;
}
Đúng 2
Bình luận (0)




