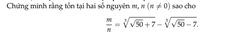Đặt \(x=\sqrt[3]{\sqrt[]{50}+7}-\sqrt[3]{\sqrt[]{50}-7}\)
\(x^3=14-3\sqrt[3]{\left(\sqrt[]{50}+7\right)\left(\sqrt[]{50}-7\right)}\left(\sqrt[3]{\sqrt[]{50}+7}-\sqrt[3]{\sqrt[]{50}-7}\right)\)
\(x^3=14-3x\)
\(x^3+3x-14=0\)
\(\left(x-2\right)\left(x^2+2x+7\right)=0\)
\(x=2\)
\(\Rightarrow\dfrac{m}{n}=2\)
\(\Rightarrow\) Hiển nhiên tồn tại vô số m, n nguyên thỏa mãn đẳng thức trên
Đúng 0
Bình luận (0)