Đặt f(x) = ax2 + bx + c

Có P(x)=3x^4+x^2+1/4

   Vì 3x^4 \(\ge\) 0  Với mọi x

         x^2 \(\ge\) 0   Với mọi x

    nên 3x^4+x^2 \(\ge\) 0 với mọi x

=>3x^4+x^2+1/4 \(\ge\) 0+1/4 >0   với mọi x

=>P(x) > với mọi x 

Vậy P(x) vô nghiệm

\(a,x^2-\left(2m-3\right)x+m^2=0-vô-ngo\)

\(\Leftrightarrow\Delta< 0\Leftrightarrow[-\left(2m-3\right)]^2-4m^2< 0\Leftrightarrow m>\dfrac{3}{4}\)

\(b,\left(m-1\right)x^2-2mx+m-2=0\)

\(m-1=0\Leftrightarrow m=1\Rightarrow-2x-1=0\Leftrightarrow x=-0,5\left(ktm\right)\)

\(m-1\ne0\Leftrightarrow m\ne1\Rightarrow\Delta'< 0\Leftrightarrow\left(-m\right)^2-\left(m-2\right)\left(m-1\right)< 0\Leftrightarrow m< \dfrac{2}{3}\)

\(c,\left(2-m\right)x^2-2\left(m+1\right)x+4-m=0\)

\(2-m=0\Leftrightarrow m=2\Rightarrow-6x+2=0\Leftrightarrow x=\dfrac{1}{3}\left(ktm\right)\)

\(2-m\ne0\Leftrightarrow m\ne2\Rightarrow\Delta'< 0\Leftrightarrow[-\left(m+1\right)]^2-\left(4-m\right)\left(2-m\right)< 0\Leftrightarrow m< \dfrac{7}{8}\)

f(x)=x²+x+1=x²+\(\dfrac{1}{2}x+\dfrac{1}{2}x+\dfrac{1}{4}+\dfrac{3}{4}\)

      =\(x\left(x+\dfrac{1}{2}\right)+\dfrac{1}{2}\left(x+\dfrac{1}{2}\right)+\dfrac{3}{4}\)

      =\(\left(x+\dfrac{1}{2}\right)\left(x+\dfrac{1}{2}\right)+\dfrac{3}{4}=\left(x+\dfrac{1}{2}\right)^{^2}+\dfrac{3}{4}\)

=>f(x)≥\(\dfrac{3}{4}\)

=>đa thức trên vô nghiệm

Bài này có nhiều cách, vừa rồi là cách cơ bản, còn nếu bạn muốn nâng cao chút thì có thể dùng cách này nha:

Xét x≥0 thì x+1>0

       x(x+1)≥0=>x(x+1)+1>0 =>x²+x+1>0                               (1)

Xét -1<x<0 thì x+1≤0. Ta lại có x²≥0 nên x²+x+1 >0                   (2)

Xét x≤-1 thì x<0 và x+1≤0. Do đó

    x(x+1) ≥0=>x(x+1) +1>0=>x²+x+1>0                           (3)

Từ (1), (2), (3)=> đa thức f(x) vô nghiệm

`***`:Cách khác  bạn dưới

`x^2+x+1=0`

`Delta=b^2-4ac`

`=1-4=-4<0`

`=>` pt vô no

Bài 2:

a: TH1: m=0

=>-x+1=0

=>x=-1(nhận)

TH2: m<>0

\(\text{Δ}=\left(m-1\right)^2-4m\left(1-m\right)\)

=m^2-2m+1-4m+4m^2

=5m^2-6m+1

=(2m-1)(3m-1)

Để phương trình có nghiệm thì (2m-1)(3m-1)>=0

=>m>=1/2 hoặc m<=1/3

b: Để phương trình có hai nghiệm phân biệt thì (2m-1)(3m-1)>0

=>m>1/2 hoặc m<1/3

c: Để phương trình có hai nghiệmtrái dấu thì (1-m)*m<0

=>m(m-1)>0

=>m>1 hoặc m<0

d: Để phương trình có hai nghiệm dương phân biệt thì

\(\left\{{}\begin{matrix}m\in\left(-\infty;\dfrac{1}{3}\right)\cup\left(\dfrac{1}{2};+\infty\right)\\\dfrac{-m+1}{m}>0\\\dfrac{1-m}{m}>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\in\left(-\infty;\dfrac{1}{3}\right)\cup\left(\dfrac{1}{2};+\infty\right)\\0< m< 1\end{matrix}\right.\)

=>1/2<m<1

\(x^2+3x+4=0\)

\(\Leftrightarrow x^2+2.x.\dfrac{3}{2}+\dfrac{9}{4}+\dfrac{7}{4}=0\)

\(\Leftrightarrow\left(x+\dfrac{3}{2}\right)^2+\dfrac{7}{4}=0\)

\(\Leftrightarrow\left(x+\dfrac{3}{2}\right)^2=-\dfrac{7}{4}\left(VL\right)\)

Vậy ĐPCM

\(x^2+3x+4=0\Leftrightarrow x^2+2.x.\dfrac{3}{2}+\dfrac{9}{4}+\dfrac{7}{4}=0\)

\(\Leftrightarrow x^2+2.x.\dfrac{3}{2}+\left(\dfrac{3}{2}\right)^2+\dfrac{7}{4}=0\Leftrightarrow\left(x+\dfrac{3}{2}\right)^2+\dfrac{7}{4}=0\)

Ta có \(\left(x+\dfrac{3}{2}\right)^2\ge0,\forall x\)

\(\Rightarrow\left(x+\dfrac{3}{2}\right)^2+\dfrac{7}{4}>0,\forall x\)

Vậy phương trình vô nghiệm.

Điều kiện xác định x ≥ –8

Ta có: 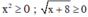 nên 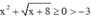 với mọi x ≥ –8.

Do đó BPT 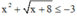 vô nghiệm.

\(x^4-6x^3+16x^2-22x+16=0\)

\(\Rightarrow x^4-2x^3+3x^2-4x^3+8x^2-12x+5x^2-10x+15+1=0\)

\(\Rightarrow x^2\left(x^2-2x+3\right)-4x\left(x^2-2x+3\right)+5\left(x^2-2x+3\right)x^2+1=0\)

\(\Rightarrow\left(x^2-2x+3\right)\left(x^2-4x+5\right)=-1\)

\(\Rightarrow\left(x^2-2x+1+2\right)\left(x^2-4x+4+1\right)=-1\)

\(\Rightarrow\left[\left(x-1\right)^2+2\right]\left[\left(x-2\right)^2+1\right]=-1\left(1\right)\)

mà \(\left\{{}\begin{matrix}\left(x-1\right)^2+2>0,\forall x\\\left(x-2\right)^2+1>0,\forall x\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}\left[\left(x-1\right)^2+2\right]\left[\left(x-2\right)^2+1\right]>0,\forall x\\\left[\left(x-1\right)^2+2\right]\left[\left(x-2\right)^2+1\right]=-1\end{matrix}\right.\) (vô lí)

Vậy phương trình trên vô nghiệm (dpcm)

a) 2(x+1)=2x-1

<=> 2x+2=2x-1

<=> 2x+2-2x+1=0

<=>1=0

=>Pt vô nghiệm