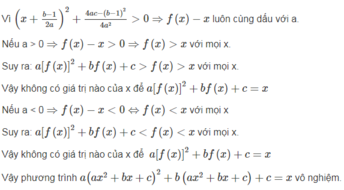Các câu hỏi tương tự
chứng minh rằng nếu phương trình \(ax^2+bx+c=x\left(a\ne0\right)\)vô nghiệm thì phương trình \(a\left(ax^2+bx+c\right)^2+b\left(ax^2+bx+c\right)+c=x\)cũng vô nghiệm
cho a,b,c là 3 số dương có tổng bằng 12
chứng minh rằng trong 3 phương trình :
x^2 + ax + b =0
x^2+bx+c = 0
x^2 + cx +a =0
có một phương trình vô nghiệm , một phương trình có nghiệm
CMR :phương trình ax^2 +bc+c=x(a#o) vô ngiệm thì pt a(ax^2+bc+c)^2+b(ax^2+bx+c)+c=x cũng vô nghiệm.
Cho hai phương trình ax2+bx+c=0(a khác 0) và mx2+nx+p=0 (m khác 0).Chứng minh rằng nếu ít nhất một trong hai phương trình trên vô nghiệm thì phương trình sau đây luôn có nghiệm (an-bm)x2 +2(ap-cm)x +bp-cn=0
Cho phương trình ax^2+bx+c0left(1right)cx^2+bx+a0left(2right)a) Chứng minh rằng 2 phương trình đã cho cùng có nghiệm hoặc cùng vô nghiệm b)Giả sử x_1,x_2 và x_1,x_2 lần lượt là các nghiệm của phương trình(1) và phương trình(2). Chứng minh rằng x_1x_2+x_1x_22
Đọc tiếp
Cho phương trình
\(ax^2+bx+c=0\left(1\right)\)
\(cx^2+bx+a=0\left(2\right)\)
a) Chứng minh rằng 2 phương trình đã cho cùng có nghiệm hoặc cùng vô nghiệm
b)Giả sử \(x_1,x_2\) và \(x'_1,x'_2\) lần lượt là các nghiệm của phương trình(1) và phương trình(2). Chứng minh rằng \(x_1x_2+x'_1x'_2>2\)
a) Chứng minh rằng với a, b , c là các số thực thì phương trình sau luôn có nghiệm:(x – a)(x – b) + (x – b)(x – c) + (x – c)(x – a) 0b) Chứng minh rằng với ba số thức a, b , c phân biệt thì phương trình sau có hai nghiệm phân biết: c) Chứng minh rằng phương trình: c2x2 + (a2 – b2 – c2)x + b2 0 vô nghiệm với a, b, c là độ dài ba cạnh của một tam giác.d) Chứng minh rằng phương trình bậc hai:(a + b)2x2 – (a – b)(a2 – b2)x – 2ab(a2 + b2) 0 luôn có hai nghiệm phân biệt.
Đọc tiếp
a) Chứng minh rằng với a, b , c là các số thực thì phương trình sau luôn có nghiệm:
(x – a)(x – b) + (x – b)(x – c) + (x – c)(x – a) = 0
b) Chứng minh rằng với ba số thức a, b , c phân biệt thì phương trình sau có hai nghiệm phân biết: 
c) Chứng minh rằng phương trình: c2x2 + (a2 – b2 – c2)x + b2 = 0 vô nghiệm với a, b, c là độ dài ba cạnh của một tam giác.
d) Chứng minh rằng phương trình bậc hai:
(a + b)2x2 – (a – b)(a2 – b2)x – 2ab(a2 + b2) = 0 luôn có hai nghiệm phân biệt.
Cho a,b,c là các số dương đôi một khác nhau sao cho a+b+c = 12. CMR trong 3 phương trình sau có 1 phương trình có nghiệm, một phương trình vô nghiệm:
\(x^2+ax+b=0\); \(x^2+bx+c=0\); \(x^2+cx+a=0\)
tìm điều kiện của a,b,c để phương trình sau vô nghiệm:
a(ax2+bx+c)2+b(ax2+bx+c)+c=x
cho a,b,c là các số dương đôi một khác nhau có tổng là 12.CMR trong ba phương trình sau có một phương trình vô nghiệm 1 phương trình có nghiệm
(1) x2+ax+b=0
(2)x2+bx+c=0
(3)x2+cx+a=0