Vì (d1)//(d) => (d1):y=x+b (\(b\ne1\))

Xét pt hoành độ gđ của (d1) và (P):

\(\dfrac{1}{2}x^2=x+b\) 

\(\Leftrightarrow x^2-2x-2b=0\)  (1)

Để (d1) và (P) tiếp xúc với nhau <=>Pt (1) có nghiệm kép <=> \(\Delta=0\)\(\Leftrightarrow4-4\left(-2b\right)=0\Leftrightarrow b=-\dfrac{1}{2}\) (thỏa)

Vậy (d1): \(y=x-\dfrac{1}{2}\)

1.

\(\left(C\right):x^2+y^2-2x-4=0\)

\(\Leftrightarrow\left(x-1\right)^2+y^2=5\)

Đường tròn \(\left(C\right)\) có tâm \(I=\left(1;0\right)\), bán kính \(R=\sqrt{5}\)

Phương trình đường thẳng \(d_1\) có dạng: \(x+y+m=0\left(m\in R\right)\)

Mà \(d_1\) tiếp xúc với \(\left(C\right)\Rightarrow d\left(I;d_1\right)=\dfrac{\left|1+m\right|}{\sqrt{2}}=\sqrt{5}\)

\(\Leftrightarrow\left|m+1\right|=\sqrt{10}\)

\(\Leftrightarrow m=-1\pm\sqrt{10}\)

\(\Rightarrow\left[{}\begin{matrix}d_1:x+y-1+\sqrt{10}=0\\d_1:x+y-1-\sqrt{10}=0\end{matrix}\right.\)

2.

Phương trình đường thẳng \(\Delta\) có dạng: \(x-y+m=0\left(m\in R\right)\)

Ta có: \(d\left(I;\Delta\right)=\sqrt{R^2-\dfrac{MN^2}{4}}=2\)

\(\Leftrightarrow\dfrac{\left|m+1\right|}{\sqrt{2}}=2\)

\(\Leftrightarrow m=-1\pm2\sqrt{2}\)

\(\Rightarrow\left[{}\begin{matrix}\Delta:x-y+1+2\sqrt{2}=0\\\Delta:x-y+1-2\sqrt{2}=0\end{matrix}\right.\)

3.

Vì \(P\in d\Rightarrow P=\left(m;m+1\right)\left(m\in R\right)\)

\(\Rightarrow IP=\sqrt{\left(m-1\right)^2+\left(m+1\right)^2}=\sqrt{2m^2+2}\)

Ta có: \(cosAIP=cos60^o=\dfrac{R}{IP}=\dfrac{\sqrt{5}}{IP}=\dfrac{1}{2}\Rightarrow IP=2\sqrt{5}\)

\(\Rightarrow\sqrt{2m^2+2}=2\sqrt{5}\)

\(\Leftrightarrow2m^2+2=20\)

\(\Leftrightarrow m=\pm3\)

\(\Rightarrow\left[{}\begin{matrix}P=\left(3;4\right)\\P=\left(-3;-2\right)\end{matrix}\right.\)

1.

Gọi \(I\left(x;y\right)\) là tâm đường tròn \(\Rightarrow\overrightarrow{AI}=\left(x-1;y-3\right)\)

Do đường tròn tiếp xúc với \(d_1;d_2\) nên:

\(d\left(I;d_1\right)=d\left(I;d_2\right)\Rightarrow\dfrac{\left|5x+y-3\right|}{\sqrt{26}}=\dfrac{\left|2x-7y+1\right|}{\sqrt{53}}\)

Chà, đề đúng ko em nhỉ, thế này thì vẫn làm được nhưng rõ ràng nhìn 2 cái mẫu kia thì số liệu sẽ xấu 1 cách vô lý.

2.

Phương trình đường thẳng kia là gì nhỉ? \(2x+y=0\) à?

b: Phương trình hoành độ giao điểm là:

\(x^2-2x+k-1=0\)

\(\text{Δ}=\left(-2\right)^2-4\left(k-1\right)=-4k+4+4=-4k+8\)

Để (P) tiếp xúc với (d) thì -4k+8=0

hay k=2

Do (d1) song song với đường thẳng y = 2x nên a = 2

(d1): y = 2x + b

Thay tọa độ điểm (1; -1) vào (d) ta được:

2.1 + b = -1

⇔ b = -1 - 2

⇔ b = -3

Vậy (d1): y = 2x - 3

b) x = 0 ⇒ y = -3

*) Đồ thị:

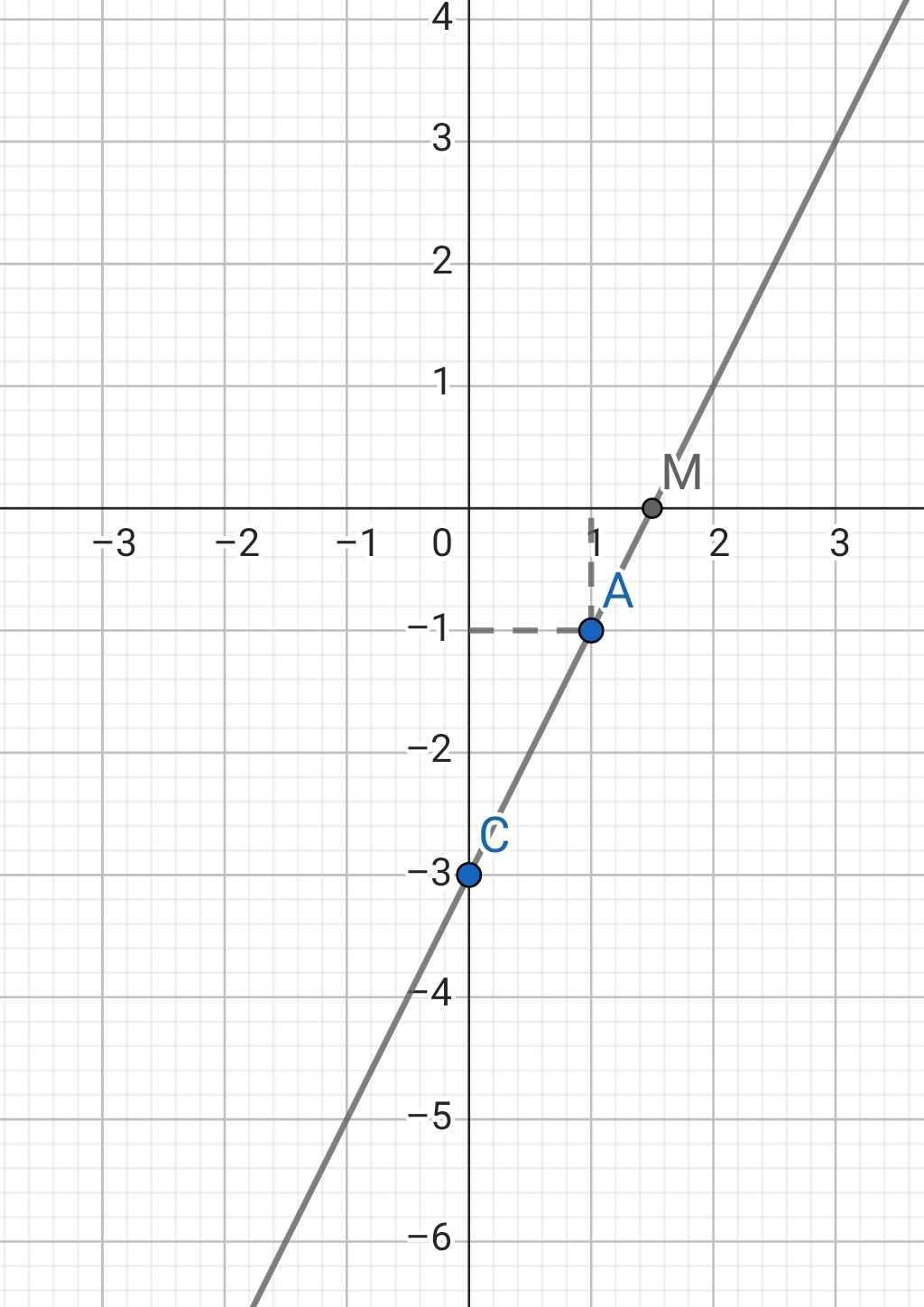
c) Phương trình hoành độ giao điểm của (d1) và (d2):

2x - 3 = 1/2 x + 1

⇔ 2x - 1/2 x = 1 + 3

⇔ 3/2 x = 4

⇔ x = 4 : 2/3

⇔ x = 8/3

⇒ y = 2.8/3 - 3 = 7/3

Vậy tọa độ giao điểm của (d1) và (d2) là (8/3; 7/3)

d) Ta có:

Gọi a là góc cần tính

⇒ tan(a) = 2

⇒ a ≈ 63⁰

(b) và (d) bạn tự xem kiến thức vẽ rồi áp dụng công thức tan là làm được nha=)

a)

Đồ thị hàm số (d₁)// đường thẳng `y=2x`

=> \(\left\{{}\begin{matrix}a=a'\\b\ne b'\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b\ne0\end{matrix}\right.\)

=> `y=2x+b`

Do hàm số `y=2x+b` đi qua điểm `(1;-1)` nên `x=1`, `y=-1`:

`-1=2.1+b`

=> `b=-3`

Vậy hàm số `y=ax+b` là `y=2x-3`

c)

Ta có PTHĐGĐ giữa `d_1` và `d_2`:

 \(2x-3=\dfrac{1}{2}x+1\\ \Rightarrow x=\dfrac{8}{3}\Rightarrow y=\dfrac{7}{3}\)

Vậy `E=`\(\left(\dfrac{8}{3};\dfrac{7}{3}\right)\)

$HaNa$

chịu  nguoi ta moi lop 6 sao giai duoc

Ai giúpe  với

a: 

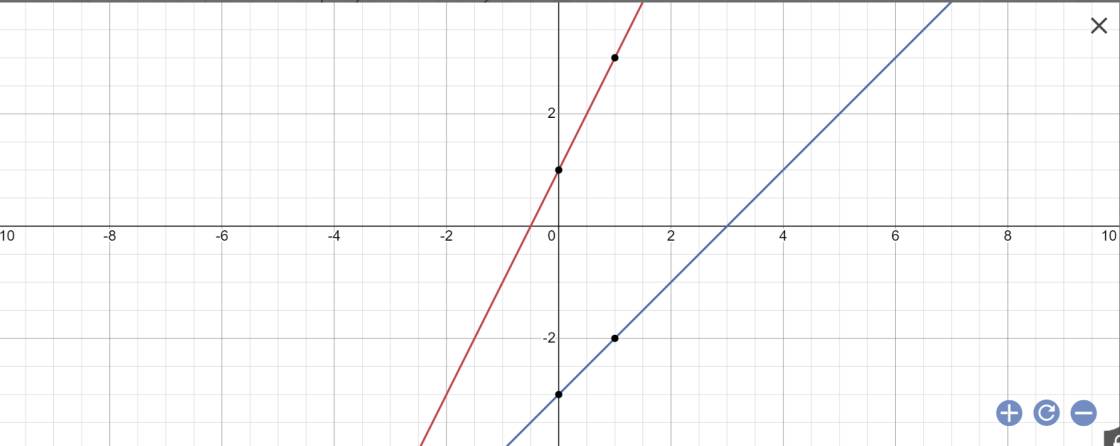
b: Phương trình hoành độ giao điểm là:

\(2x+1=x-3\)

=>\(2x-x=-3-1\)

=>x=-4

Thay x=-4 vào y=x-3, ta được:

\(y=-4-3=-7\)

Vậy: Tọa độ giao điểm của (D1) và (D2) là B(-4;-7)

c: Đặt phương trình đường thẳng (d3): y=ax+b

Vì (d3)//(d1) nên \(\left\{{}\begin{matrix}a=2\\b< >1\end{matrix}\right.\)

Vậy: y=2x+b

Thay x=1 và y=0 vào y=2x+b, ta được:

\(b+2\cdot1=0\)

=>b+2=0

=>b=-2

Vậy: (d): y=2x-2

b: Phương trình hoành độ giao điểm là:

\(2x+2=\dfrac{-1}{2}x-2\)

\(\Leftrightarrow x\cdot\dfrac{5}{2}=-4\)

hay x=-10

Thay x=-10 vào (d1), ta được:

\(y=-20+2=-18\)

\(c,\left(d_3\right)\) đi qua \(A\left(-10;-18\right)\) nên \(x=-10;y=-18\)

\(\left(d_3\right)\) có dạng \(y=ax+b\Leftrightarrow-18=-10a+b\left(1\right)\)

\(\left(d_3\right)//y=-5x+2\Leftrightarrow\left\{{}\begin{matrix}a=-5\\b\ne2\end{matrix}\right.\)

Thay vào \(\left(1\right)\Leftrightarrow-18=-10\left(-5\right)+b\Leftrightarrow b=32\left(tm\right)\)

Vậy \(\left(d_3\right):y=-5x+32\)