a: Thay m=1 vào hệ phương trình, ta được:

\(\left\{{}\begin{matrix}x-y=1\\2x+y=4\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}3x=5\\x-y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{3}\\y=x-1=\dfrac{5}{3}-1=\dfrac{2}{3}\end{matrix}\right.\)

b: Để hệ có nghiệm duy nhất thì \(\dfrac{m}{2}\ne-\dfrac{1}{m}\)

=>\(m^2\ne-2\)(luôn đúng)

\(\left\{{}\begin{matrix}mx-y=1\\2x+my=4\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=mx-1\\2x+m\left(mx-1\right)=4\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=mx-1\\x\left(m^2+2\right)=m+4\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=\dfrac{m+4}{m^2+2}\\y=\dfrac{m\left(m+4\right)}{m^2+2}-1=\dfrac{m^2+4m-m^2-2}{m^2+2}=\dfrac{4m-2}{m^2+2}\end{matrix}\right.\)

x+y=2

=>\(\dfrac{m+4+4m-2}{m^2+2}=2\)

=>\(2m^2+4=5m+2\)

=>\(2m^2-5m+2=0\)

=>(2m-1)(m-2)=0

=>\(\left[{}\begin{matrix}2m-1=0\\m-2=0\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}m=\dfrac{1}{2}\\m=2\end{matrix}\right.\)

Hệ đã cho vô nghiệm khi

\(m+2=\dfrac{m+1}{3}\ne\dfrac{3}{4}\Leftrightarrow m=-\dfrac{5}{2}\)

Chọn D

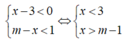
Hệ bất phương trình vô nghiệm  khi và chỉ khi m - 1 ≥ 3 hay m ≥ 4

`a,x-3y=2`

`<=>x=3y+2` ta thế vào phương trình trên:

`2(3y+2)+my=-5`

`<=>6y+4+my=-5`

`<=>y(m+6)=-9`

HPT có nghiệm duy nhất:

`<=>m+6 ne 0<=>m ne -6`

HPT vô số nghiệm

`<=>m+6=0,-6=0` vô lý `=>x in {cancel0}`

HPT vô nghiệm

`<=>m+6=0,-6 ne 0<=>m ne -6`

b,HPT có nghiệm duy nhất

`<=>m ne -6`(câu a)

`=>y=-9/(m+6)`

`<=>x=3y+2`

`<=>x=(-27+2m+12)/(m+6)`

`<=>x=(-15+2m)/(m+6)`

`x+2y=1`

`<=>(2m-15)/(m+6)+(-18)/(m+6)=1`

`<=>(2m-33)/(m+6)=1`

`2m-33=m+6`

`<=>m=39(TM)`

Vậy `m=39` thì HPT có nghiệm duy nhất `x+2y=1`

b)Ta có: \(\left\{{}\begin{matrix}2x+my=-5\\x-3y=2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=2+3y\\2\left(2+3y\right)+my=-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2+3y\\6y+my+4=-5\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=3y+2\\y\left(m+6\right)=-9\end{matrix}\right.\)

Khi \(m\ne6\) thì \(y=-\dfrac{9}{m+6}\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=3y+2\\y=\dfrac{-9}{m+6}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\cdot\dfrac{-9}{m+6}+2\\y=-\dfrac{9}{m+6}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{-27}{m+6}+\dfrac{2m+12}{m+6}=\dfrac{2m-15}{m+6}\\y=\dfrac{-9}{m+6}\end{matrix}\right.\)

Để hệ phương trình có nghiệm duy nhất thỏa mãn x+2y=1 thì \(\dfrac{2m-15}{m+6}+\dfrac{-18}{m+6}=1\)

\(\Leftrightarrow2m-33=m+6\)

\(\Leftrightarrow2m-m=6+33\)

hay m=39

Vậy: Khi m=39 thì hệ phương trình có nghiệm duy nhất thỏa mãn x+2y=1

2: \(\text{Δ}=1^2-4\cdot\left(-1\right)\cdot\left(-m\right)=1-4m\)

Để bất phương trình vô nghiệm thì \(\left\{{}\begin{matrix}1-4m< 0\\-1< 0\end{matrix}\right.\Leftrightarrow m>\dfrac{1}{4}\)

\(\Leftrightarrow\left(m^2+2m+1\right)x-\left(7m-5\right)x=m-1\)

\(\Leftrightarrow\left(m^2-5m+6\right)x=m-1\)

Pt vô nghiệm khi: \(\left\{{}\begin{matrix}m^2-5m+6=0\\m-1\ne0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}m=2\\m=3\end{matrix}\right.\)