Thực hiện phép tính:
\(\dfrac{x+7}{x-7}-\dfrac{x-7}{x+7}+\dfrac{4x^2}{x^2-49}\)
Thực hiện phép tính :
a/ (x - 1)^2 - (4x + 3) (2 - x)
b/ (15x^3y^2 - 6x^2y^3) : 3x^2y^2 = (15x^3y^2 : 3x^2y^2) - (6x^2y^3 : 3x^2y^2) = 5x - 2y
c/\(\dfrac{x+7}{x-7}\) - \(\dfrac{x-7}{x+7}\) +\(\dfrac{4x^2}{x^2-49}\)
a/ (x-1)2-(4x+3)(2-x)=x2-2x+1-(8x-4x2+6-3x)
=x2-2x+1-8x+4x2-6+3x=5x2-7x-6
b/ (15x3y2 - 6x2y3) : 3x2y2 = 5x - 2y
c/ \(\dfrac{x+7}{x-7}-\dfrac{x-7}{x+7}+\dfrac{4x^2}{x^2-49}\)=\(\dfrac{\left(x+7\right)^2-\left(x-7\right)^2+4x^2}{\left(x-7\right)\left(x+7\right)}\)=\(\dfrac{x^2+14x+49-\left(x^2-14x+49\right)+4x^2}{\left(x-7\right)\left(x+7\right)}\)=\(\dfrac{28x+4x^2}{\left(x-7\right)\left(x+7\right)}\)=\(\dfrac{4x\left(x+7\right)}{\left(x-7\right)\left(x+7\right)}\)=\(\dfrac{4x}{x-7}\)
Câu 1: Thực hiện phép tính
\(\dfrac{3}{7}x^2< 28x^5-7^3-\dfrac{14}{3}x^2-2\)
Dùng quy tắc đổi dấu rồi thực hiện các phép tính :
a) \(\dfrac{4x+13}{5x\left(x-7\right)}-\dfrac{x-48}{5x\left(7-x\right)}\)
b) \(\dfrac{1}{x-5x^2}-\dfrac{25x-15}{25x^2-1}\)
Bài 1:Thực hiện phép tính
a)(16x3y2-24x2y3+20x4):16x2
b)(x2-49):(x-7)
Bài 2:Quy đồng mẫu thức 2 phân thức sau:
\(\dfrac{1}{a^2}\)-ab và \(\dfrac{1}{a^2}\)
Bài 3:RG phân thức sau:
\(\dfrac{7\left(t-z\right)}{t\left(z-t\right)}\)
Bài 4:Tính:
\(\dfrac{x-1}{y-x}\)+\(\dfrac{1-y}{x-y}\)
Giúp mình với ạ:))
\(1,\\ a,=xy^2-\dfrac{3}{2}y^3+\dfrac{5}{4}x^2\\ b,=\left(x-7\right)\left(x+7\right):\left(x-7\right)=x+7\\ 2,\dfrac{1}{a^2}-ab=\dfrac{1-a^3b}{a^2};\dfrac{1}{a^2}\text{ giữ nguyên}\\ 3,=\dfrac{-7}{t}\\ 4,=\dfrac{1-x+1-y}{x-y}=\dfrac{2-x-y}{x-y}\)
Bài 1:
\(a,\left(16x^3y^2-24x^2y^3+20x^4\right):16x^2=16x^2\left(xy^2-\dfrac{3}{2}y^3+\dfrac{5}{4}x^2\right):16x^2=xy^2-\dfrac{3}{2}y^3+\dfrac{5}{4}x^2\)
\(b,\left(x^2-49\right):\left(x-7\right)=\left[\left(x-7\right)\left(x+7\right)\right]:\left(x-7\right)=x+7\)
Bài 2:
\(\dfrac{1}{a^2}-ab=\dfrac{1-a^2b}{a^2}\)
\(\dfrac{1}{a^2}\)
Bài 3:
\(\dfrac{7\left(t-z\right)}{t\left(z-t\right)}=\dfrac{-7\left(z-t\right)}{t\left(z-t\right)}=\dfrac{-7}{t}\)
Bài 4:
\(\dfrac{x-1}{y-x}+\dfrac{1-y}{x-y}=\dfrac{x-1}{y-x}-\dfrac{1-y}{y-x}=\dfrac{x-1-1+y}{y-x}=\dfrac{x+y-2}{y-x}\)
Thực hiện các phép tính sau :
a) \(\dfrac{3x-5}{7}+\dfrac{4x+5}{7}\)
b) \(\dfrac{5xy-4y}{2x^2y^3}+\dfrac{3xy+4y}{2x^2y^3}\)
c) \(\dfrac{x+1}{x-5}+\dfrac{x-18}{x-5}+\dfrac{x+2}{x-5}\)
thực hiện phép tính
\(\dfrac{x}{x-3}-\dfrac{6}{x}-\dfrac{9}{x^2-3x}\)
\(\dfrac{7}{x}-\dfrac{x}{x+6}+\dfrac{36}{x^2+6x}\)
\(\dfrac{6}{x-3}-\dfrac{2x-16}{x^2-9}-\dfrac{4}{x+3}\)
a) Ta có: \(\dfrac{x}{x-3}-\dfrac{6}{x}-\dfrac{9}{x^2-3x}\)
\(=\dfrac{x^2}{x\left(x-3\right)}-\dfrac{6\left(x-3\right)}{x\left(x-3\right)}-\dfrac{9}{x\left(x-3\right)}\)
\(=\dfrac{x^2-6x+18-9}{x\left(x-3\right)}\)
\(=\dfrac{\left(x-3\right)^2}{x\left(x-3\right)}=\dfrac{x-3}{x}\)
b) Ta có: \(\dfrac{7}{x}-\dfrac{x}{x+6}+\dfrac{36}{x^2+6x}\)
\(=\dfrac{7\left(x+6\right)-x^2+36}{x\left(x+6\right)}\)
\(=\dfrac{7x+42-x^2+36}{x\left(x+6\right)}\)
\(=\dfrac{-\left(x^2-7x-78\right)}{x\left(x+6\right)}\)
\(=\dfrac{-\left(x^2-13x+6x-78\right)}{x\left(x+6\right)}\)
\(=\dfrac{-\left[x\left(x-13\right)+6\left(x-13\right)\right]}{x\left(x+6\right)}\)
\(=\dfrac{13-x}{x}\)
c) Ta có: \(\dfrac{6}{x-3}-\dfrac{2x-6}{x^2-9}-\dfrac{4}{x+3}\)
\(=\dfrac{6\left(x+3\right)-2x+6-4\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{6x+18-2x+6-4x+12}{\left(x-3\right)\left(x+3\right)}=\dfrac{36}{\left(x-3\right)\left(x+3\right)}\)
a, cho A = \(\dfrac{\sqrt{x+1}}{\sqrt{x-3}}\). tìm x để A có giá trị nguyên ( x ϵ Z)
b, Thực hiện phép tính: {[(2\(\sqrt{2}\))\(^2\) : 2,4] x [5,25 : (\(\sqrt{7}\))\(^2\)]} : {[2\(\dfrac{1}{7}\) : \(\dfrac{\left(\sqrt{5}\right)^2}{7}\)] : [2\(^2\) : \(\dfrac{\left(2\sqrt{2}\right)^2}{\sqrt{81}}\)]}
a: Sửa đề: \(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)
ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\ne9\end{matrix}\right.\)
Để A là số nguyên thì \(\sqrt{x}+1⋮\sqrt{x}-3\)
=>\(\sqrt{x}-3+4⋮\sqrt{x}-3\)
=>\(4⋮\sqrt{x}-3\)
=>\(\sqrt{x}-3\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(\sqrt{x}\in\left\{4;2;5;1;7;-1\right\}\)
=>\(\sqrt{x}\in\left\{4;2;5;1;7\right\}\)
=>\(x\in\left\{16;4;25;1;49\right\}\)
b: 
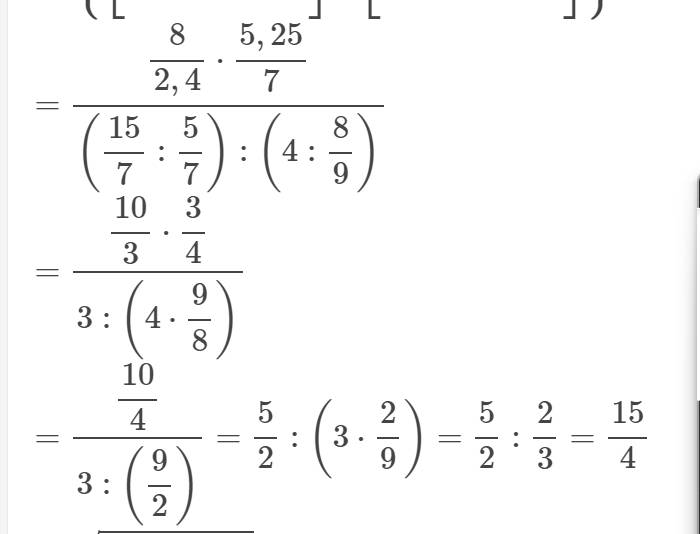
thực hiện phép tính \(\dfrac{x+7}{x^2-x-6}+\dfrac{x+10}{x^2+x-2}+\dfrac{\left(x-7\right)}{x^2-4x+3}\)
\(=\dfrac{x+7}{\left(x-3\right)\left(x+2\right)}+\dfrac{x+10}{\left(x+2\right)\left(x-1\right)}+\dfrac{x-7}{\left(x-1\right)\left(x-3\right)}\)
\(=\dfrac{x^2+6x-7+x^2+7x-30+x^2-5x-14}{\left(x-1\right)\left(x-3\right)\left(x+2\right)}\)
\(=\dfrac{3x^2+8x-51}{\left(x-1\right)\left(x-3\right)\left(x+2\right)}\)
\(=\dfrac{3x^2-9x+17x-51}{\left(x-1\right)\left(x-3\right)\left(x+2\right)}=\dfrac{\left(3x+17\right)}{\left(x-1\right)\left(x+2\right)}\)
Thực hiên các phép tính
a,\(\dfrac{x-1}{x^2-5x+4}\) - \(\dfrac{4}{x^2-4x}\)
b,\(\dfrac{x}{x+2}\) + \(\dfrac{7x-16}{\left(x+2\right)\left(7x-7\right)}\)
\(a,đk:x\ne0;4;1\)
\(\dfrac{x-1}{x^2-5x+4}-\dfrac{4}{x^2-4x}\\ =\dfrac{x-1}{\left(x-1\right)\left(x-4\right)}-\dfrac{4}{x\left(x-4\right)}\\ =\dfrac{x\left(x-1\right)}{x\left(x-1\right)\left(x-4\right)}-\dfrac{4\left(x-1\right)}{x\left(x-1\right)\left(x-4\right)}\\ =\dfrac{x^2-x-4x+4}{x\left(x-1\right)\left(x-4\right)}\\ =\dfrac{x^2-5x+4}{x.\left(x-1\right)\left(x-4\right)}=\dfrac{\left(x-1\right)\left(x-4\right)}{x.\left(x-1\right)\left(x-4\right)}=\dfrac{1}{x}\)
\(đk:x\ne-2;1\)
\(\dfrac{x}{x+2}+\dfrac{7x-16}{\left(x+2\right)\left(7x-7\right)}\\ =\dfrac{x\left(7x-7\right)}{\left(x+2\right)\left(7x-7\right)}+\dfrac{7x-16}{\left(x+2\right)\left(7x-7\right)}\\ =\dfrac{7x^2-7x+7x-16}{\left(x+2\right)\left(7x-7\right)}\\ =\dfrac{7x^2-16}{\left(x+2\right)\left(7x-7\right)}\)
a)
\(\dfrac{x-1}{x^2-5x+4}-\dfrac{4}{x^2-4x}\) \(ĐKXĐ:x\ne0;x\ne4;x\ne1\)
\(=\dfrac{x-1}{x^2-4x-x+4}-\dfrac{4}{x\left(x-4\right)}\)
\(=\dfrac{x-1}{x\left(x-4\right)-\left(x-4\right)}-\dfrac{4}{x\left(x-4\right)}\)
\(=\dfrac{x-1}{\left(x-1\right)\left(x-4\right)}-\dfrac{4}{x\left(x-4\right)}\)
\(=\dfrac{x^2-x}{x\left(x-1\right)\left(x-4\right)}-\dfrac{4\left(x-1\right)}{x\left(x-1\right)\left(x-4\right)}\)
\(=\dfrac{x^2-x-4x+4}{x\left(x-1\right)\left(x-4\right)}\)
\(=\dfrac{x\left(x-1\right)-4\left(x-1\right)}{x\left(x-1\right)\left(x-4\right)}\)
\(=\dfrac{\left(x-1\right)\left(x-4\right)}{x\left(x-1\right)\left(x-4\right)}\\ =\dfrac{1}{x}\)
b)
\(\dfrac{x}{x+2}+\dfrac{7x-16}{\left(x+2\right)\left(7x-7\right)}\) \(ĐKXĐ:x\ne-2;x\ne1\)
\(=\dfrac{x\left(7x-7\right)}{\left(x+2\right)\left(7x-7\right)}+\dfrac{7x-16}{\left(x+2\right)\left(7x-7\right)}\)
\(=\dfrac{7x^2-7x+7x-16}{\left(x+2\right)\left(7x-7\right)}\)
\(=\dfrac{7x^2-16}{\left(x+2\right)\left(7x-7\right)}\)
Bài 1: Thực hiện phép tính
a, (5x-2y)(x\(^2\)-xy+1)
b, (x-1)(x+1)(x+2)
c, \(\dfrac{1}{2}\)x\(^2\)y\(^2\)(2x+y)(2x-y)
d, (x-\(\dfrac{1}{2}\))(x+\(\dfrac{1}{2}\))(4x-1)
e, (x-7)(x+5)-(2x+1)(3-x)
a: =5x^3-5x^2y+5x-2x^2y+2xy^2-2y
=5x^3-7x^2y+2xy^2+5x-2y
b: =(x^2-1)(x+2)
=x^3+2x^2-x-2
c: =1/2x^2y^2(4x^2-y^2)
=2x^4y^2-1/2x^2y^4
d: =(x^2-1/4)(4x-1)
=4x^3-x^2-x+1/4
e: =x^2-2x-35+(2x+1)(x-3)
=x^2-2x-35+2x^2-6x+x-3
=3x^2-7x-38