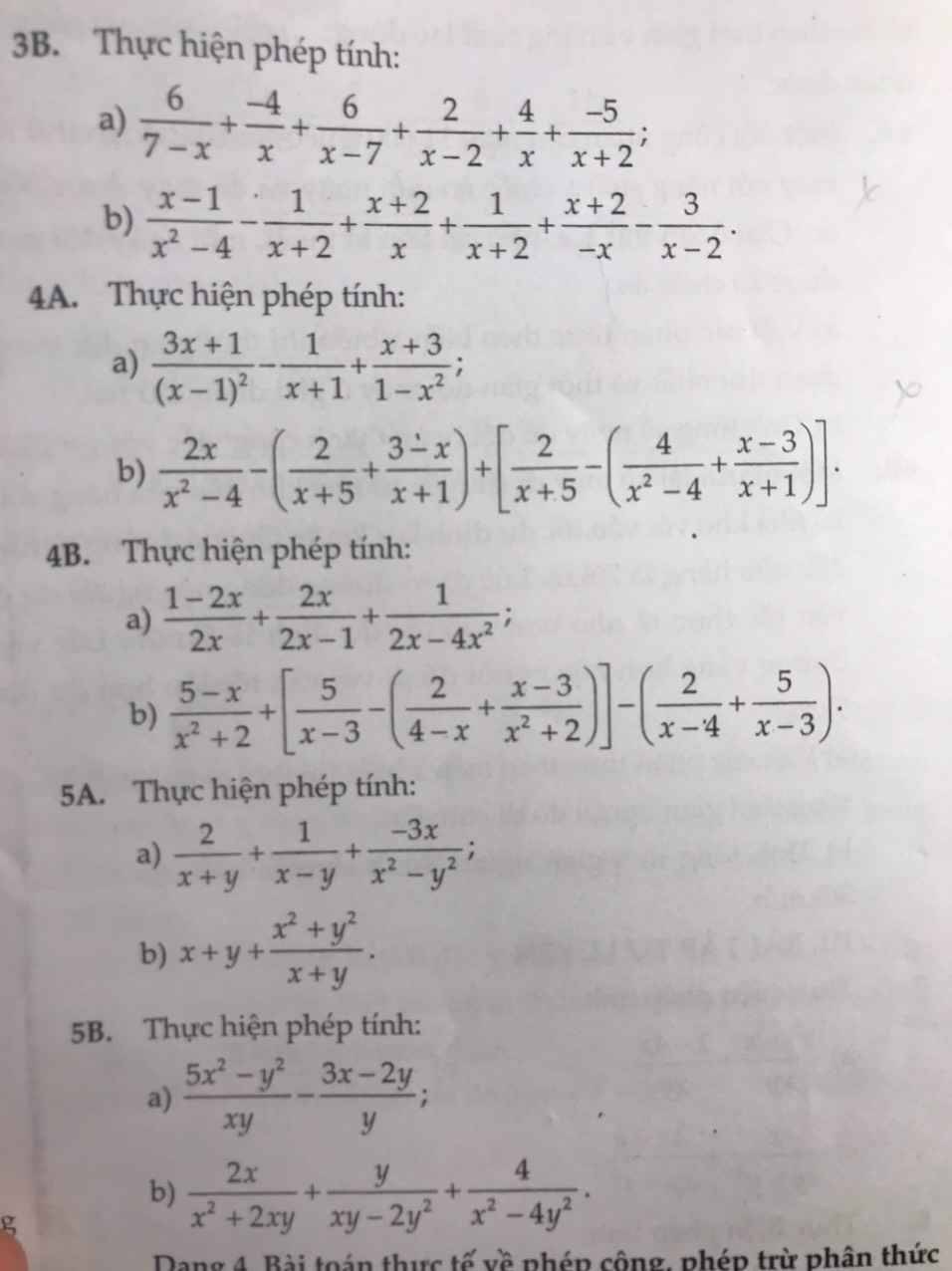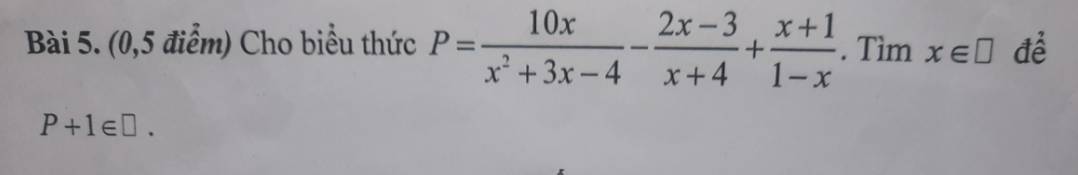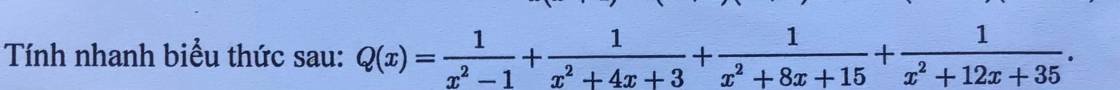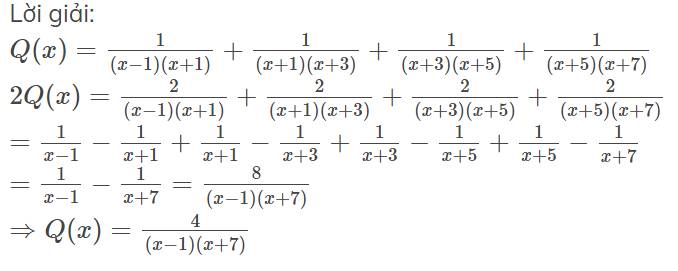Bài 5: Phép cộng các phân thức đại số

a: \(\dfrac{2x}{5}+\dfrac{2}{5}=\dfrac{2x+2}{5}\)

b: \(\dfrac{2x+5}{3}+\dfrac{x-2}{3}\)

\(=\dfrac{2x+5+x-2}{3}\)

\(=\dfrac{3x+3}{3}=x+1\)

c: ĐKXĐ: \(x\ne1\)

\(\dfrac{5x}{x-1}+\dfrac{x+1}{x-1}\)

\(=\dfrac{5x+x+1}{x-1}\)

\(=\dfrac{6x+1}{x-1}\)

2/x²y + x/3x²y²

= 2.3y/3x²y² + x/3x²y²

= (6y + x)/3x²y²

Bạn cần hỗ trợ bài nào bạn nên ghi chú rõ ra nhé. Nếu cần nhiều bài, nên tách lẻ 1-2 bài / post để mọi người hỗ trợ nhanh hơn.

5A:
a: ĐKXĐ: \(x\ne\pm y\)

\(\dfrac{2}{x+y}+\dfrac{1}{x-y}+\dfrac{-3x}{x^2-y^2}\)

\(=\dfrac{2}{x+y}+\dfrac{1}{x-y}-\dfrac{3x}{\left(x-y\right)\left(x+y\right)}\)

\(=\dfrac{2\left(x-y\right)+x+y-3x}{\left(x+y\right)\left(x-y\right)}\)

\(=\dfrac{2x-2y-2x+y}{\left(x+y\right)\left(x-y\right)}=-\dfrac{y}{\left(x+y\right)\left(x-y\right)}\)

b: ĐKXĐ: x<>-y

\(x+y+\dfrac{x^2+y^2}{x+y}\)

\(=\dfrac{\left(x+y\right)^2+x^2+y^2}{x+y}\)

\(=\dfrac{x^2+2xy+y^2+x^2+y^2}{x+y}=\dfrac{2x^2+2xy+2y^2}{x+y}\)

5B:

a: ĐKXĐ: \(\left\{{}\begin{matrix}x\ne0\\y\ne0\end{matrix}\right.\)

\(\dfrac{5x^2-y^2}{xy}-\dfrac{3x-2y}{y}\)

\(=\dfrac{5x^2-y^2-x\left(3x-2y\right)}{xy}\)

\(=\dfrac{5x^2-y^2-3x^2+2xy}{xy}\)

\(=\dfrac{2x^2+2xy-y^2}{xy}\)

b: ĐKXĐ: \(\left\{{}\begin{matrix}x\ne0\\y\ne0\\x\ne\pm2y\end{matrix}\right.\)

\(\dfrac{2x}{x^2+2xy}+\dfrac{y}{xy-2y^2}+\dfrac{4}{x^2-4y^2}\)

\(=\dfrac{2x}{x\left(x+2y\right)}+\dfrac{y}{y\left(x-2y\right)}+\dfrac{4}{\left(x-2y\right)\cdot\left(x+2y\right)}\)

\(=\dfrac{2}{x+2y}+\dfrac{1}{x-2y}+\dfrac{4}{\left(x-2y\right)\left(x+2y\right)}\)

\(=\dfrac{2x-4y+x+2y+4}{\left(x+2y\right)\left(x-2y\right)}=\dfrac{3x-2y+4}{\left(x-2y\right)\left(x+2y\right)}\)

\(\left(a+b+c\right)^2=a^2+b^2+c^2\)

=>\(a^2+b^2+c^2+2\left(ab+bc+ac\right)=a^2+b^2+c^2\)

=>\(2\left(ab+bc+ac\right)=0\)

=>ab+bc+ac=0

\(\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{1}{c^3}=\dfrac{3}{abc}\)

=>\(\dfrac{\left(bc\right)^3+\left(ac\right)^3+\left(ab\right)^3}{\left(abc\right)^3}=\dfrac{3}{abc}\)

=>\(\left(bc\right)^3+\left(ac\right)^3+\left(ab\right)^3=3\left(abc\right)^2\)

\(\Leftrightarrow\left(ab+bc\right)^3-3\cdot ab\cdot bc\cdot\left(ab+bc\right)+\left(ac\right)^3=3\left(abc\right)^2\)

=>\(\left(-ac\right)^3-3\cdot ab\cdot bc\cdot\left(-ac\right)+\left(ac\right)^3-3\left(abc\right)^2=0\)

=>\(-a^3c^3+a^3c^3+3a^2b^2c^2-3a^2b^2c^2=0\)

=>0=0(đúng)

\(P=\dfrac{10x}{x^2+3x-4}-\dfrac{2x-3}{x+4}+\dfrac{x+1}{1-x}\) \(\left(x\ne1;x\ne-4\right)\)

\(P=\dfrac{10x}{\left(x+4\right)\left(x-1\right)}-\dfrac{2x-3}{x+4}-\dfrac{x+1}{x-1}\)

\(P=\dfrac{10x}{\left(x+4\right)\left(x-1\right)}-\dfrac{\left(2x-3\right)\left(x-1\right)}{\left(x+4\right)\left(x-1\right)}-\dfrac{\left(x+1\right)\left(x+4\right)}{\left(x-1\right)\left(x+4\right)}\)

\(P=\dfrac{10x-2x^2+2x+3x-3-x^2-x-4x-4}{\left(x+4\right)\left(x-1\right)}\)

\(P=\dfrac{-3x^2+10x-7}{\left(x+4\right)\left(x-1\right)}\)

\(P=\dfrac{-3\left(x+1\right)\left(x-1\right)}{\left(x+4\right)\left(x-1\right)}\)

\(P=\dfrac{-3x-3}{x+4}\)

\(P=\dfrac{-3x-12+9}{x+4}\)

\(P=\dfrac{9}{x+4}-3\)

P nguyên khi \(\dfrac{9}{x+4}\) nguyên

\(\Rightarrow x+4\in\left\{1;-1;3;-3;9;-9\right\}\)

\(\Rightarrow x\in\left\{-3;-5;-1;-7;5;-13\right\}\)

\(Q\left(x\right)=\dfrac{1}{x^2-1}+\dfrac{1}{x^2+4x+3}+\dfrac{1}{x^2+8x+15}+\dfrac{1}{x^2+12x+35}\)

\(=\dfrac{1}{\left(x-1\right)\left(x+1\right)}+\dfrac{1}{x^2+x+3x+3}+\dfrac{1}{x^2+3x+5x+15}+\dfrac{1}{x^2+5x+7x+35}\)

\(=\dfrac{1}{\left(x-1\right)\left(x+1\right)}+\dfrac{1}{x\left(x+1\right)+3\left(x+1\right)}+\dfrac{1}{x\left(x+3\right)+5\left(x+3\right)}+\dfrac{1}{x\left(x+5\right)+7\left(x+5\right)}\)

\(=\dfrac{1}{\left(x-1\right)\left(x+1\right)}+\dfrac{1}{\left(x+1\right)\left(x+3\right)}+\dfrac{1}{\left(x+3\right)\left(x+5\right)}+\dfrac{1}{\left(x+5\right)\left(x+7\right)}\)

\(=\dfrac{1}{2}\cdot\left[\dfrac{2}{\left(x-1\right)\left(x+1\right)}+\dfrac{2}{\left(x+1\right)\left(x+3\right)}+\dfrac{2}{\left(x+3\right)\left(x+5\right)}+\dfrac{2}{\left(x+5\right)\left(x+7\right)}\right]\)

\(=\dfrac{1}{2}\cdot\left(\dfrac{1}{x-1}-\dfrac{1}{x+1}+\dfrac{1}{x+1}-\dfrac{1}{x+3}+\dfrac{1}{x+3}-\dfrac{1}{x+5}+\dfrac{1}{x+5}-\dfrac{1}{x+7}\right)\)

\(=\dfrac{1}{2}\cdot\left(\dfrac{1}{x-1}-\dfrac{1}{x+7}\right)\)

\(=\dfrac{1}{2}\cdot\dfrac{x+7-\left(x-1\right)}{\left(x-1\right)\left(x+7\right)}\)

\(=\dfrac{1}{2}\cdot\dfrac{8}{\left(x-1\right)\left(x+7\right)}\)

\(=\dfrac{4}{\left(x-1\right)\left(x+7\right)}\)

\(=\dfrac{4}{x^2+6x-7}\)

#\(Toru\)

a) \(\dfrac{1}{x+2}+\dfrac{5}{2x^2+3x-2}\)

\(=\dfrac{1}{x+2}+\dfrac{5}{2x^2+4x-x-2}\)

\(=\dfrac{2x-1}{\left(2x-1\right)\left(x+2\right)}+\dfrac{5}{2x\left(x+2\right)-\left(x+2\right)}\)

\(=\dfrac{2x-1+5}{\left(2x-1\right)\left(x+2\right)}\)

\(=\dfrac{2x+4}{\left(2x-1\right)\left(x+2\right)}\)

\(=\dfrac{2\left(x+2\right)}{\left(2x-1\right)\left(x+2\right)}\)

\(=\dfrac{2}{2x-1}\)

\(---\)

b) \(\dfrac{-3x^2}{x^3+1}+\dfrac{1}{x^2-x+1}+\dfrac{1}{x+1}\) (sửa đề)

\(=\dfrac{-3x^2}{\left(x+1\right)\left(x^2-x+1\right)}+\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}+\dfrac{x^2-x+1}{\left(x+1\right)\left(x^2-x+1\right)}\)

\(=\dfrac{-3x^2+x+1+x^2-x+1}{\left(x+1\right)\left(x^2-x+1\right)}\)

\(=\dfrac{-2x^2+2}{\left(x+1\right)\left(x^2-x+1\right)}\)

\(=\dfrac{-2\left(x^2-1\right)}{\left(x+1\right)\left(x^2-x+1\right)}\)

\(=\dfrac{-2\left(x-1\right)\left(x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}\)

\(=\dfrac{-2x+2}{x^2-x+1}\)

\(---\)

c) \(\dfrac{1}{1-x}+\dfrac{1}{1+x}+\dfrac{2}{1+x^2}+\dfrac{4}{1+x^4}\)

\(=\dfrac{1+x}{\left(1-x\right)\left(1+x\right)}+\dfrac{1-x}{\left(1-x\right)\left(1+x\right)}+\dfrac{2}{1+x^2}+\dfrac{4}{1+x^4}\)

\(=\dfrac{1+x+1-x}{1^2-x^2}+\dfrac{2}{1+x^2}+\dfrac{4}{1+x^4}\)

\(=\dfrac{2}{1-x^2}+\dfrac{2}{1+x^2}+\dfrac{4}{1+x^4}\)

\(=\dfrac{2\left(1+x^2\right)}{\left(1-x^2\right)\left(1+x^2\right)}+\dfrac{2\left(1-x^2\right)}{\left(1-x^2\right)\left(1+x^2\right)}+\dfrac{4}{1+x^4}\)

\(=\dfrac{2+2x^2+2-2x^2}{1-x^4}+\dfrac{4}{1+x^4}\)

\(=\dfrac{4}{1-x^4}+\dfrac{4}{1+x^4}\)

\(=\dfrac{4\left(1+x^4\right)}{\left(1-x^4\right)\left(1+x^4\right)}+\dfrac{4\left(1-x^4\right)}{\left(1-x^4\right)\left(1+x^4\right)}\)

\(=\dfrac{4+4x^4+4-4x^4}{1-x^8}\)

\(=\dfrac{8}{1-x^8}\)

#\(Toru\)

\(\dfrac{1}{x+2}+\dfrac{5}{2x^2+3x-2}\\ =\dfrac{1}{x+2}+\dfrac{5}{\left(2x-1\right)\left(x+2\right)}\\ =\dfrac{2x-1}{\left(2x-1\right)\left(x+2\right)}+\dfrac{5}{\left(2x-1\right)\left(x+2\right)}\\ =\dfrac{2x-1+5}{\left(2x-1\right)\left(x+2\right)}\\ =\dfrac{2x+4}{\left(2x-1\right)\left(x+2\right)}\\ =\dfrac{2\left(x+2\right)}{\left(2x-1\right)\left(x+2\right)}\\ =\dfrac{2}{2x-1}\)

__

`x^3+1` chứ cậu nhỉ?

\(\dfrac{-3x^2}{x^3+1}+\dfrac{1}{x^2-x+1}+\dfrac{1}{x+1}\\ =\dfrac{-3x^2}{\left(x+1\right)\left(x^2-x+1\right)}+\dfrac{1}{x^2-x+1}+\dfrac{1}{x+1}\\ =\dfrac{-3x^2}{\left(x+1\right)\left(x^2-x+1\right)}+\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}+\dfrac{x^2-x+1}{\left(x-1\right)\left(x^2-x+1\right)}\\ =\dfrac{-3x^2+x+1+x^2-x+1}{\left(x+1\right)\left(x^2-x+1\right)}\\ =\dfrac{-2x^2+2}{\left(x+1\right)\left(x^2-x+1\right)}\\ =\dfrac{-2\left(x^2-1\right)}{\left(x+1\right)\left(x^2-x+1\right)}\)

\(=\dfrac{-2\left(x-1\right)\left(x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}\\ =\dfrac{-2\left(x-1\right)}{x^2-x+1}\)

__

Biểu thức nào nhỉ cậu?

Lời giải:
$Q(x)=\frac{1}{(x-1)(x+1)}+\frac{1}{(x+1)(x+3)}+\frac{1}{(x+3)(x+5)}+\frac{1}{(x+5)(x+7)}$

$2Q(x)=\frac{2}{(x-1)(x+1)}+\frac{2}{(x+1)(x+3)}+\frac{2}{(x+3)(x+5)}+\frac{2}{(x+5)(x+7)}$

$=\frac{1}{x-1}-\frac{1}{x+1}+\frac{1}{x+1}-\frac{1}{x+3}+\frac{1}{x+3}-\frac{1}{x+5}+\frac{1}{x+5}-\frac{1}{x+7}$

$=\frac{1}{x-1}-\frac{1}{x+7}=\frac{8}{(x-1)(x+7)}$

$\Rightarrow Q(x)=\frac{4}{(x-1)(x+7)}$

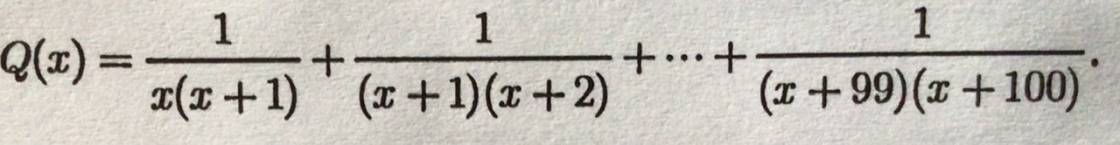
\(Q\left(x\right)=\dfrac{1}{x\left(x+1\right)}+\dfrac{1}{\left(x+1\right)\left(x+2\right)}+...+\dfrac{1}{\left(x+99\right)\left(x+100\right)}\)

\(=\dfrac{1}{x}-\dfrac{1}{x+1}+\dfrac{1}{x+1}-\dfrac{1}{x+2}+...+\dfrac{1}{x+99}-\dfrac{1}{x+100}\)

\(=\dfrac{1}{x}-\dfrac{1}{x+100}\)

\(=\dfrac{x+100-x}{x\left(x+100\right)}\)

\(=\dfrac{100}{x\left(x+100\right)}\)

#\(Toru\)

Câu 2: