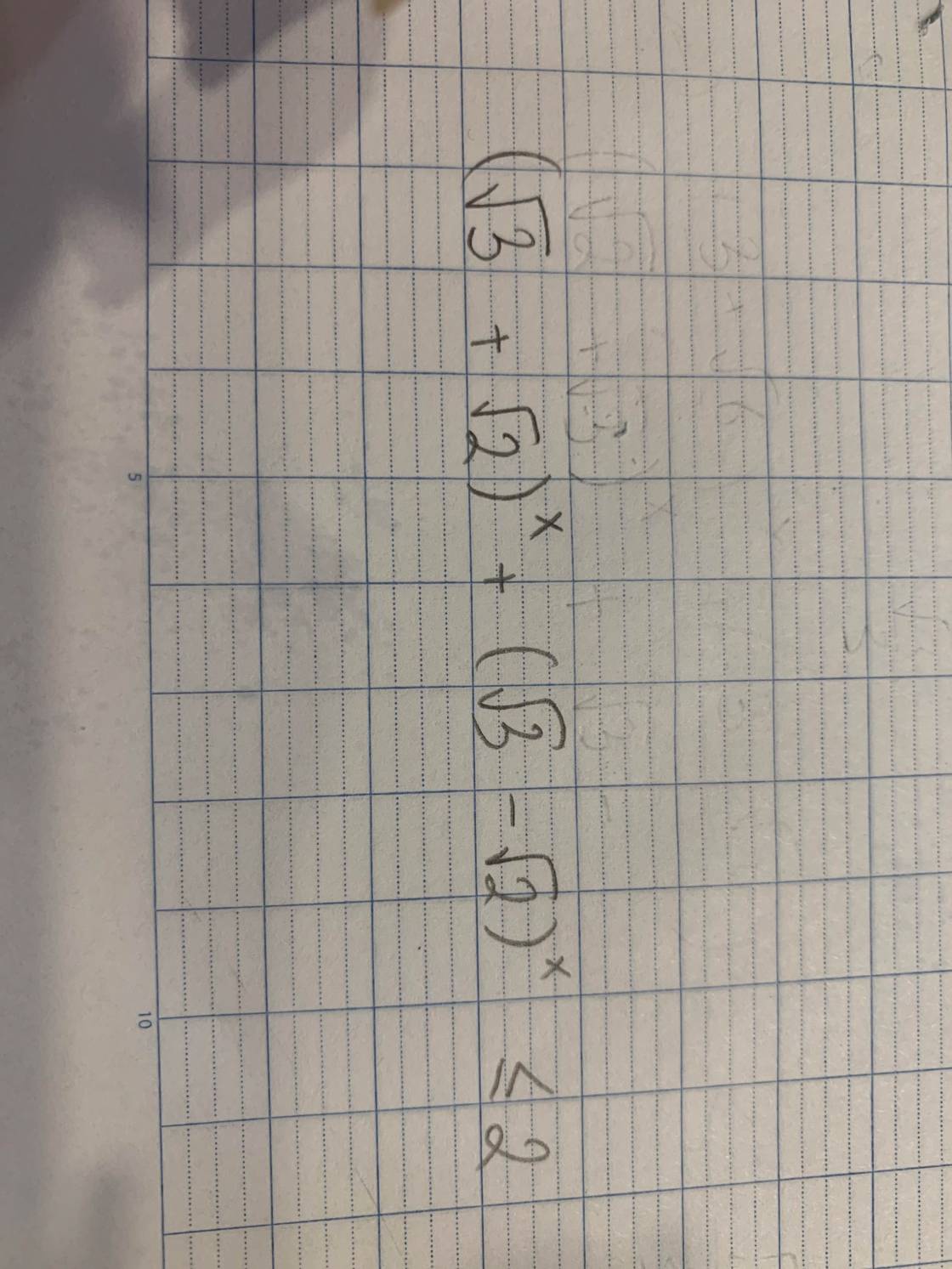a.

\(\Leftrightarrow\dfrac{\sqrt{2}}{2}sin4x+\dfrac{\sqrt{2}}{2}cos4x=\dfrac{\sqrt{6}}{2}\)

\(\Leftrightarrow cos4x.cos\left(\dfrac{\pi}{4}\right)+sin4x.sin\left(\dfrac{\pi}{4}\right)=\dfrac{\sqrt{6}}{2}\)

\(\Leftrightarrow cos\left(4x-\dfrac{\pi}{4}\right)=\dfrac{\sqrt{6}}{2}\)

\(\Leftrightarrow\left[{}\begin{matrix}4x-\dfrac{\pi}{4}=arccos\left(\dfrac{\sqrt{6}}{2}\right)+k2\pi\\4x-\dfrac{\pi}{4}=-arccos\left(\dfrac{\sqrt{6}}{2}\right)+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{16}+\dfrac{1}{4}arccos\left(\dfrac{\sqrt{6}}{2}\right)+\dfrac{k\pi}{4}\\x=\dfrac{\pi}{16}-\dfrac{1}{4}arccos\left(\dfrac{\sqrt{6}}{2}\right)+\dfrac{k\pi}{4}\end{matrix}\right.\)

b.

\(\Leftrightarrow\dfrac{\sqrt{3}}{2}sinx+\dfrac{1}{2}cosx=\dfrac{\sqrt{3}}{6}\)

\(\Leftrightarrow cosx.cos\left(\dfrac{\pi}{3}\right)+sinx.sin\left(\dfrac{\pi}{3}\right)=\dfrac{\sqrt{3}}{6}\)

\(\Leftrightarrow cos\left(x-\dfrac{\pi}{3}\right)=\dfrac{\sqrt{3}}{6}\)

\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{3}=arccos\left(\dfrac{\sqrt{3}}{6}\right)+k2\pi\\x-\dfrac{\pi}{3}=-arccos\left(\dfrac{\sqrt{3}}{6}\right)+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+arccos\left(\dfrac{\sqrt{3}}{6}\right)+k2\pi\\x=\dfrac{\pi}{3}-arrcos\left(\dfrac{\sqrt{3}}{6}\right)+k2\pi\end{matrix}\right.\)

c.

\(\Leftrightarrow\dfrac{\sqrt{3}}{2}cosx+\dfrac{1}{2}sinx=-\dfrac{\sqrt{2}}{2}\)

\(\Leftrightarrow cosx.cos\left(\dfrac{\pi}{6}\right)+sinx.sin\left(\dfrac{\pi}{6}\right)=cos\left(\dfrac{3\pi}{4}\right)\)

\(\Leftrightarrow cos\left(x-\dfrac{\pi}{6}\right)=cos\left(\dfrac{3\pi}{4}\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{6}=\dfrac{3\pi}{4}+k2\pi\\x-\dfrac{\pi}{6}=-\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{11\pi}{12}+k2\pi\\x=-\dfrac{7\pi}{12}+k2\pi\end{matrix}\right.\)

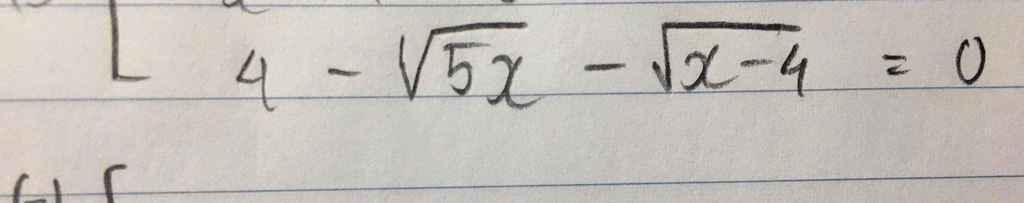
ĐKXĐ:\(x\ge4\)

\(4-\sqrt{5x}-\sqrt{x-4}=0\\ \Leftrightarrow4-\sqrt{5x}=\sqrt{x-4}\left(x\le\dfrac{16}{5}\right)\)

Vì \(x\ge4\) mà \(x\le\dfrac{16}{5}\) (vô lí)

\(\Rightarrow\) pt vô nghiệm

1d->yet

2a->has already been

3a->Studying

4b->was

5c->knows

6c->developed

7a->Did you eat

8d->properly

\(Errink \times Cream\)

a: ΔOBC cân tại O

mà OA là đường cao

nên OA là phân giác của góc BOC

Xét ΔOBA và ΔOCA có

OB=OC

\(\widehat{BOA}=\widehat{COA}\)

OA chung

Do đó: ΔOBA=ΔOCA

=>\(\widehat{OBA}=\widehat{OCA}=90^0\)

=>AC là tiếp tuyến của (O)

b: Ta có: \(\widehat{KOA}+\widehat{BOA}=\widehat{KOB}=90^0\)

\(\widehat{KAO}+\widehat{COA}=90^0\)(ΔOCA vuông tại C)

mà \(\widehat{BOA}=\widehat{COA}\)

nên \(\widehat{KOA}=\widehat{KAO}\)

=>KA=KO

d: Xét (O) có

\(\widehat{ACI}\) là góc tạo bởi tiếp tuyến CA và dây cung CI

\(\widehat{CDI}\) là góc nội tiếp chắn cung CI

Do đó: \(\widehat{ACI}=\widehat{CDI}\)

ΔOCA vuông tại C

=>\(CO^2+CA^2=OA^2\)

=>\(CA^2=\left(2R\right)^2-R^2=3R^2\)

=>\(CA=R\sqrt{3}\)

Xét ΔACI và ΔADC có

\(\widehat{ACI}=\widehat{ADC}\)

\(\widehat{CAI}\) chung

Do đó: ΔACI đồng dạng với ΔADC

=>\(\dfrac{AC}{AI}=\dfrac{AD}{AC}\)

=>\(AI\cdot AD=AC^2=\left(R\sqrt{3}\right)^2=3R^2\) không đổi

Xét tg ABO và tg ACO có

AO chung 

AB=AC (gt)

OB=OC=R

=> tg ABO = tg ACO (c.c.c)

\(\Rightarrow\widehat{ACO}=\widehat{ABO}=90^o\Rightarrow AC\perp OC\) => AC là tiếp tuyến với (O)

b/

Xét tg vuông EOI và tg vuông COI có

OE=OC=R; OI chung => tg EOI = tg COI (hai tg vuông có 2 cạnh góc vuông bằng nhau)

Xét tg vuông EDI và tg vuông CDI có

DI chung 

tg EOI = tg COI (cmt) => IE=IC

=> tg EDI = tg CDI (hai tg vuông có 2 cạnh góc vuông bằng nhau)

Xét tg DEO và tg DCO có

DO chung

OE=OC=R

tg EDI = tg CDI (cmt) => DE=DC

=> tg DEO = tg DCO (c.c.c)

\(\Rightarrow\widehat{DEO}=\widehat{DCO}=90^o\Rightarrow DE\perp OE\) => DE là tiếp tuyến với (O, R)

Bạn cần bài nào :v?

Em đăng tách bài nha 1-2 bài/1 lần hỏi