Giúp em với ạ!!!!

Giúp em với ạ!!!!

Đặt \(log_2x=t\)
\(t^2-4t+m+1< 0\) có \(t_1< t_2\le10\)
\(\Rightarrow\left\{{}\begin{matrix}\Delta'=3-m>0\\t_2=2+\sqrt[]{3-m}\le10\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m< 3\\m\ge-61\end{matrix}\right.\)
\(\Rightarrow\) Có 64 giá trị nguyên của m (chắc đề ghi nhầm "nguyên" thành "thực")
Giải bất phương trình: \((x-3)^{2x^2-7x}>1\)
ĐKXĐ: \(x>3\)
Lấy logarit 2 vế: \(\left(2x^2-7x\right).ln\left(x-3\right)>0\)
\(\Leftrightarrow x\left(2x-7\right)ln\left(x-3\right)>0\)
Bảng xét dấu:
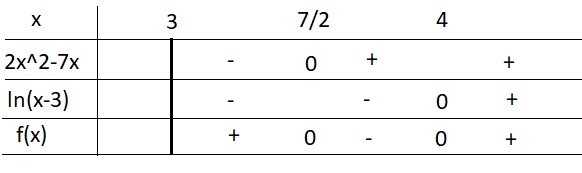
\(\Rightarrow\) Nghiệm của BPT là \(\left[{}\begin{matrix}3< x< \dfrac{7}{2}\\x>4\end{matrix}\right.\)
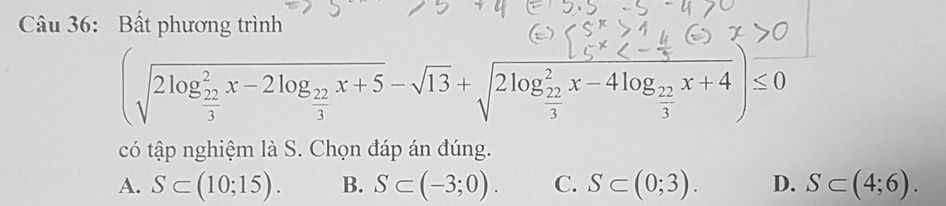
mng giúp mình vs ạ:(((
ĐKXĐ: \(x>0\)
Đặt \(\log_\frac{22}{3}x=t\) BPT trở thành:
\(\sqrt{2t^2-2t+5}-\sqrt{13}+\sqrt{2t^2-4t+4}\le0\)
\(\Leftrightarrow\sqrt{4t^2-4t+10}+\sqrt{4t^2-8t+8}\le\sqrt{26}\)
\(\Leftrightarrow\sqrt{\left(2t-1\right)^2+9}+\sqrt{\left(2-2t\right)^2+4}\le\sqrt{26}\) (1)
Ta có:
\(\sqrt{\left(2t-1\right)^2+3^2}+\sqrt{\left(2-2t\right)^2+2^2}\ge\sqrt{\left(2t-1+2-2t\right)+\left(3+2\right)^2}=\sqrt{26}\) (2)
(1);(2) \(\Rightarrow\sqrt{\left(2t-1\right)^2+9}+\sqrt{\left(2t-2\right)^2+4}=\sqrt{26}\)
Đẳng thức xảy ra khi và chỉ khi:
\(\dfrac{2t-1}{2-2t}=\dfrac{3}{2}\Rightarrow t=\dfrac{4}{5}\)
\(\Rightarrow \log_\frac{22}{3}x=\dfrac{4}{5}\)
\(\Rightarrow x=\left( \dfrac{22}{3}\right)^\frac{4}{5}\) \(\approx4,923\)
D là đáp án đúng
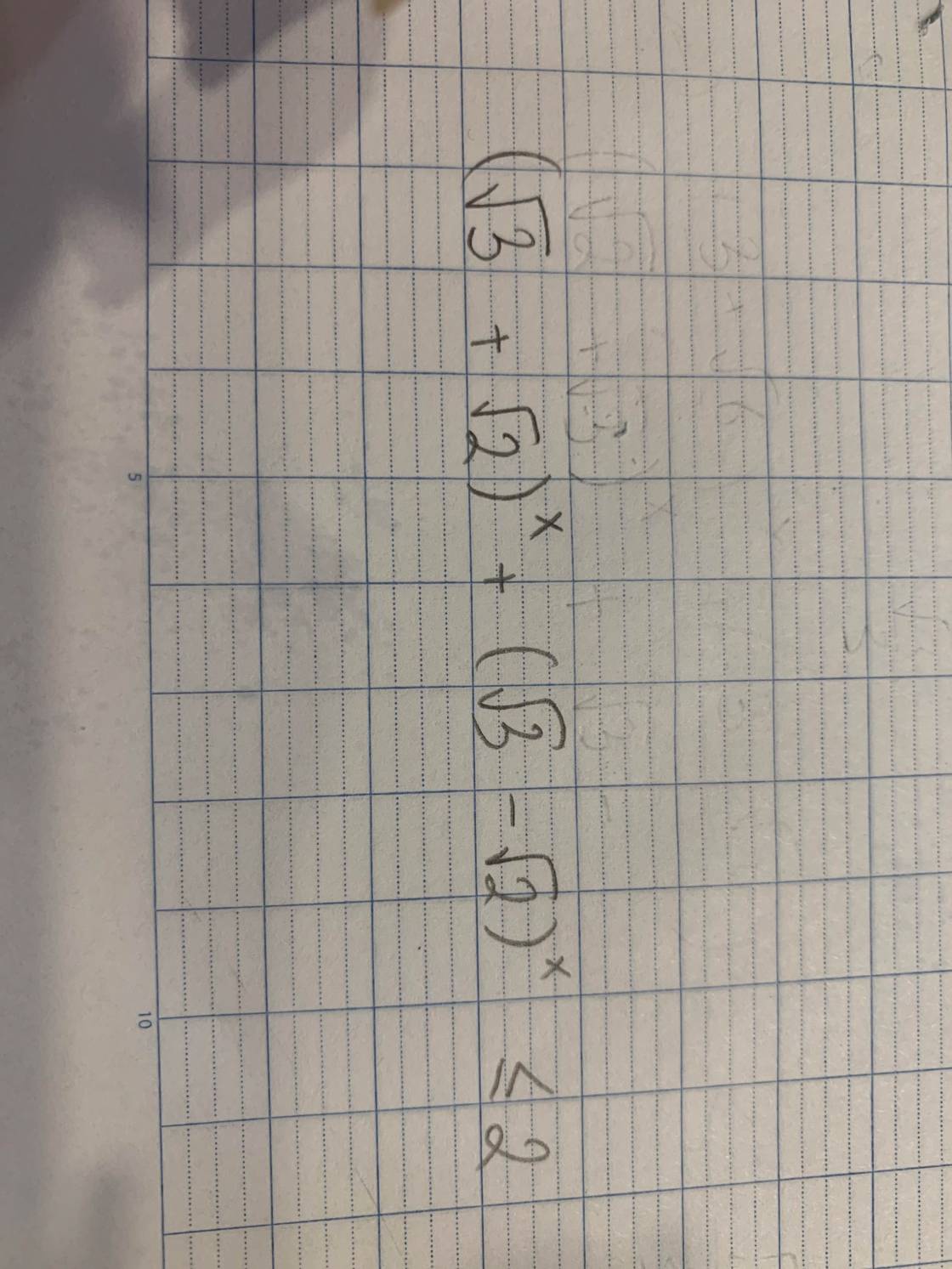 giải giúp mình bài này với ạa
giải giúp mình bài này với ạa
Đặt \(\left(\sqrt{3}+\sqrt{2}\right)^x=t>0\Rightarrow\left(\sqrt{3}-\sqrt{2}\right)^x=\dfrac{1}{t}\)
BPT trở thành:
\(t+\dfrac{1}{t}\le2\)
\(\Leftrightarrow t^2-2t+1\le0\)
\(\Leftrightarrow\left(t-1\right)^2\le0\)
\(\Rightarrow t-1=0\)
\(\Rightarrow t=1\)
\(\Rightarrow\left(\sqrt{3}+\sqrt{2}\right)^x=1\)
\(\Rightarrow x=0\)
giải bất phương trình 3 mũ x+2-3 mũ 2-x>24
\(3^{x+2}-3^{2-x}>24\)
\(\Leftrightarrow9.3^x-9.3^{-x}>24\)
Đặt \(3^x=t>0\)
\(\Rightarrow9t-\dfrac{9}{t}>24\)
\(\Leftrightarrow3t^2-8t-3>0\)
\(\Leftrightarrow\left(t-3\right)\left(3t+1\right)>0\)
\(\Leftrightarrow t>3\)
\(\Rightarrow3^x>3\)
\(\Rightarrow x>1\)
có bao nhiêu số nguyên x sao cho ứng với mỗi x tồn tại ít nhất 4 số nguyên y∈(-10;10) thỏa mãn 5x^2+y ≤4y-x+26 ? mọi người giúp mình giải chi tiết bài này với ạaa
Giải pt \(\log_2^2x-log_24x+2=0\)
ĐKXĐ: \(x>0\)
\(log_2^2x-log_2x-log_24+2=0\)
\(\Leftrightarrow log_2^2x-log_2x=0\)
\(\Leftrightarrow log_2x\left(log_2x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}log_2x=0\\log_2x=1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
Tập nghiệm của bất pt \(\log_{\dfrac{1}{2}}\left(x+1\right)-log_{\dfrac{1}{2}}\left(2x-1\right)< 2\)
ĐKXĐ: \(x>\dfrac{1}{2}\)
\(log_{\dfrac{1}{2}}\left(\dfrac{x+1}{2x-1}\right)< 2\)
\(\Rightarrow\dfrac{x+1}{2x-1}>\dfrac{1}{4}\)
\(\Rightarrow x>-\dfrac{5}{2}\)
Kết hợp ĐKXĐ: \(\Rightarrow x>\dfrac{1}{2}\)
Giải bất phương trình: \(x\left(3log_2x-2\right)>9log_2x-2\)