Giải pt sau : 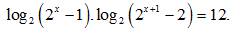
NL
Những câu hỏi liên quan
giải pt sau để pt vô nghiệm
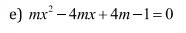
\(\text{∆}=\left(-4m\right)^2-4.m.\left(4m-1\right)\)
\(=16m^2-16m^2+4m\)
\(=4m\)
phương trình vô nghiệm khi \(\text{∆}< 0\)
\(\Rightarrow4m< 0\)
⇒ \(m< 0\)
Đúng 4
Bình luận (0)
`\Delta'=(-2m)^2-m(4m-1)=4m^2-4m^2+m=m`
Để phương trình vô nghiệm thì `\Delta'<0 => m<0`
Đúng 3
Bình luận (0)
nhận xét , đánh giá việc thực hành tiết kiệm của bản thân và những người xung quanh , phê phán những biểu hiện lãng phí
Đúng 1
Bình luận (0)
Bài 1:
a) Giải PT sau: \(\dfrac{x+1}{x-2}-\dfrac{5}{x+2}=\dfrac{12}{x^2-4}+1\)
b) Giải PT sau: |2x+6|-x=3
a) ĐKXĐ: \(x\notin\left\{2;-2\right\}\)
Ta có: \(\dfrac{x+1}{x-2}-\dfrac{5}{x+2}=\dfrac{12}{x^2-4}+1\)
\(\Leftrightarrow\dfrac{\left(x+1\right)\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}-\dfrac{5\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}=\dfrac{12}{\left(x-2\right)\left(x+2\right)}+\dfrac{x^2-4}{\left(x-2\right)\left(x+2\right)}\)
Suy ra: \(x^2+3x+2-5x+10=12+x^2-4\)
\(\Leftrightarrow x^2-2x+12-8-x^2=0\)
\(\Leftrightarrow-2x+4=0\)
\(\Leftrightarrow-2x=-4\)
hay x=2(loại)
Vậy: \(S=\varnothing\)
Đúng 2
Bình luận (0)
b) Ta có: \(\left|2x+6\right|-x=3\)
\(\Leftrightarrow\left|2x+6\right|=x+3\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+6=x+3\left(x\ge-3\right)\\-2x-6=x+3\left(x< -3\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-x=3-6\\-2x-x=3+6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\left(nhận\right)\\x=-3\left(loại\right)\end{matrix}\right.\)
Vậy: S={-3}
Đúng 1
Bình luận (0)
giải pt sau
Đọc tiếp
giải pt sau
\(ĐK:x+y\ne0;y\ne1\\ HPT\Leftrightarrow\left\{{}\begin{matrix}\dfrac{8}{x+y}+\dfrac{2}{y-1}=10\left(1\right)\\\dfrac{1}{x+y}-\dfrac{2}{y-1}=-1\left(2\right)\end{matrix}\right.\\ \left(1\right)+\left(2\right)=\dfrac{9}{x+y}=9\\ \Leftrightarrow x+y=1\Leftrightarrow x=1-y\\ \text{Thay vào }\left(2\right)\Leftrightarrow1-\dfrac{2}{y-1}=-1\\ \Leftrightarrow\dfrac{2}{y-1}=2\Leftrightarrow y-1=1\Leftrightarrow y=2\left(tm\right)\\ \Leftrightarrow x=-1\left(tm\right)\)
Vậy \(\left(x;y\right)=\left(-1;2\right)\)
Đúng 2
Bình luận (0)
Giải pt sau
Đọc tiếp
Giải pt sau
Ta có: \(\sqrt{3x^2-2x+1}=x+1\)
\(\Leftrightarrow3x^2-2x+1=x^2+2x+1\)
\(\Leftrightarrow2x^2-4x=0\)
\(\Leftrightarrow2x\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Giải pt sau
Đọc tiếp
Giải pt sau
Ta có: \(\sqrt{2x^2-5x-4}=\sqrt{4x+1}\)
\(\Leftrightarrow2x^2-5x-4=4x+1\)
\(\Leftrightarrow2x^2-9x-5=0\)
\(\Leftrightarrow2x^2-10x+x-5=0\)
\(\Leftrightarrow\left(x-5\right)\left(2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-\dfrac{1}{2}\end{matrix}\right.\)
Đúng 2
Bình luận (0)
giải pt sau 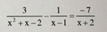
\(\LeftrightarrowĐkxđ:x\ne-2;x\ne1\\ \Leftrightarrow\dfrac{3-\left(x+2\right)+7\left(x-1\right)}{\left(x+2\right)\left(x-1\right)}=0\\ \Leftrightarrow\dfrac{-6+6x}{\left(x+2\right)\left(x-1\right)}=0\Rightarrow x=1\left(ktm\right)\)
Đúng 5
Bình luận (0)
\(ĐK:x\ne1;x\ne-2\)
\(\Leftrightarrow\dfrac{3}{\left(x-1\right)\left(x+2\right)}=-\dfrac{7}{x+2}+\dfrac{1}{x-1}\)
\(\Leftrightarrow\dfrac{3}{\left(x-1\right)\left(x+2\right)}=\dfrac{-7\left(x-1\right)+\left(x-2\right)}{\left(x-1\right)\left(x+2\right)}\)
\(\Leftrightarrow3=-7\left(x-1\right)+\left(x-2\right)\)
\(\Leftrightarrow3=-7x+7+x-2\)
\(\Leftrightarrow-6x=-2\)
\(\Leftrightarrow x=\dfrac{1}{3}\left(tm\right)\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
giải pt sau
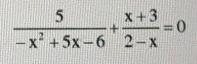
\(\Leftrightarrow5+\left(x+3\right)\left(x-3\right)=0\\ \Leftrightarrow5+x^2-9=0\\ \Leftrightarrow x^2-4=0\Rightarrow x^2=4\Rightarrow x=\pm2\)
Đúng 2
Bình luận (4)
\(ĐK:x\ne2,3\)
\(\Leftrightarrow\dfrac{5}{\left(x-3\right)\left(2-x\right)}+\dfrac{x+3}{2-x}=0\)
\(\Leftrightarrow\dfrac{5+\left(x+3\right)\left(x-3\right)}{\left(x-3\right)\left(2-x\right)}=0\)
\(\Leftrightarrow5+x^2-9=0\)
\(\Leftrightarrow x^2=4\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\left(ktm\right)\\x=-2\left(tm\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Giải pt sau: 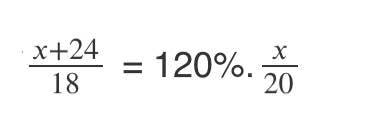
Giải hệ pt sau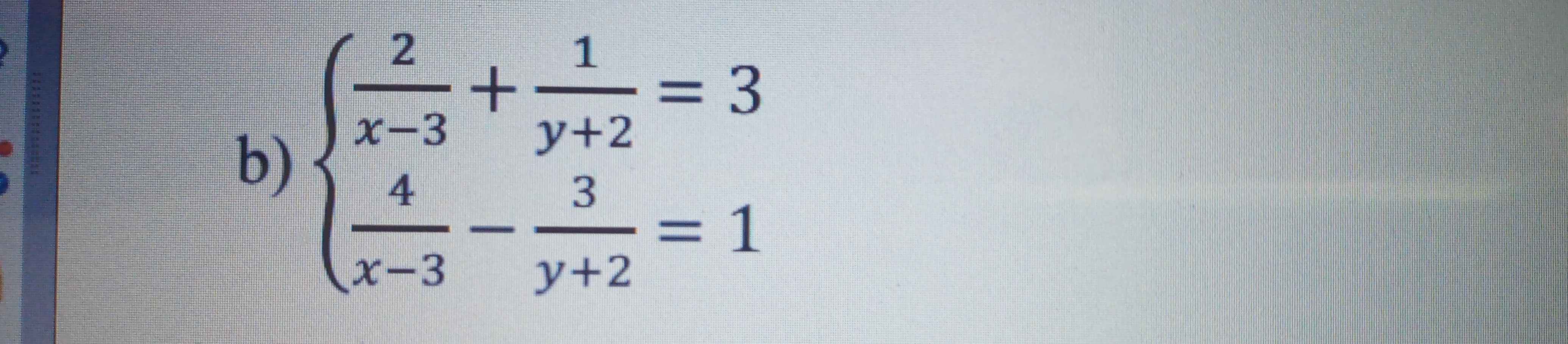
Đặt \(\dfrac{1}{x-3}=a;\dfrac{1}{y+2}=b\)
Hệ phương trình trở thành:
\(\left\{{}\begin{matrix}2a+b=3\\4a-3b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-3=1\\y+2=1\end{matrix}\right.\Leftrightarrow\left(x,y\right)=\left(4;-1\right)\)
Đúng 0
Bình luận (0)
giải hệ pt sau
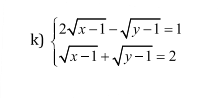
ĐKXĐ: \(x\ge1;y\ge1\)
\(\left\{{}\begin{matrix}2\sqrt{x-1}-\sqrt{y-1}=1\\\sqrt{x-1}+\sqrt{y-1}=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3\sqrt{x-1}=3\\\sqrt{x-1}+\sqrt{y-1}=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x-1}=1\\\sqrt{x-1}+\sqrt{y-1}=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x-1}=1\\\sqrt{y-1}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-1=1\\y-1=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=2\end{matrix}\right.\)
Đúng 2
Bình luận (0)







