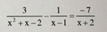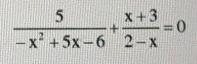\(\LeftrightarrowĐkxđ:x\ne-2;x\ne1\\ \Leftrightarrow\dfrac{3-\left(x+2\right)+7\left(x-1\right)}{\left(x+2\right)\left(x-1\right)}=0\\ \Leftrightarrow\dfrac{-6+6x}{\left(x+2\right)\left(x-1\right)}=0\Rightarrow x=1\left(ktm\right)\)
\(ĐK:x\ne1;x\ne-2\)
\(\Leftrightarrow\dfrac{3}{\left(x-1\right)\left(x+2\right)}=-\dfrac{7}{x+2}+\dfrac{1}{x-1}\)
\(\Leftrightarrow\dfrac{3}{\left(x-1\right)\left(x+2\right)}=\dfrac{-7\left(x-1\right)+\left(x-2\right)}{\left(x-1\right)\left(x+2\right)}\)
\(\Leftrightarrow3=-7\left(x-1\right)+\left(x-2\right)\)
\(\Leftrightarrow3=-7x+7+x-2\)
\(\Leftrightarrow-6x=-2\)
\(\Leftrightarrow x=\dfrac{1}{3}\left(tm\right)\)
\(\dfrac{3}{x^2+x-2}-\dfrac{x+2}{x^2+x-2}-\dfrac{-7x+7}{x^2+x-2}\) ĐK:x≠-2;x≠1
\(\Leftrightarrow3-x-2+7x-7=0\)
\(\Leftrightarrow6x=6\)
\(\Leftrightarrow x=1\)