Tìm phương trình tiếp tuyến y= x-2/x+1 biết tiếp tuyến song song với d : y=3x-2
HN
Những câu hỏi liên quan
Cho hàm số \(y=\dfrac{-1}{3x^2+x+2}\) có đồ thị (C). Viết phương trình tiếp tuyến biết:
a) Có hệ số góc bằng 1
b) Tiếp tuyến song song với Δ có phương trình \(y=-3x+2\)
c) Tiếp tuyến vuông góc với phương trình x+8y+1=0
Cho hàm số: \(y=\dfrac{x-1}{x+1}\) Viết phương trình tiếp tuyến của đồ thị hàm số biết tiếp tuyến song song với d: \(y=\dfrac{x-2}{2}\)
Ta có : \(y=\dfrac{x-1}{x+1}\Rightarrow y'=\dfrac{\left(x+1\right)-\left(x-1\right)}{\left(x+1\right)^2}=\dfrac{2}{\left(x+1\right)^2}\)
Giả sử d' là tiếp tuyến của đths đã cho . Do d' // d : y = \(\dfrac{x-2}{2}\)
\(\Rightarrow d'\) có HSG = 1/2 \(\Rightarrow\dfrac{2}{\left(x+1\right)^2}=\dfrac{1}{2}\Leftrightarrow4=\left(x+1\right)^2\) \(\Leftrightarrow\left[{}\begin{matrix}x+1=2\\x+1=-2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\)
Với x = 1 . PTTT d' : \(y=\dfrac{1}{2}\left(x-1\right)+0=\dfrac{1}{2}x-\dfrac{1}{2}\)
Với x = -3 . PTTT d' : \(y=\dfrac{1}{2}\left(x+3\right)+2=\dfrac{1}{2}x+\dfrac{7}{2}\)
Đúng 2
Bình luận (0)
Cho hàm số: \(y=\dfrac{x-1}{x+1}\) Viết phương trình tiếp tuyến của đồ thị hàm số biết tiếp tuyến song song với d: \(y=\dfrac{x-2}{2}\)
y'=(x-1)'(x+1)-(x-1)(x+1)'/(x+1)^2=(x+1-x+1)/(x+1)^2=2/(x+1)^2
(d1)//(d)
=>(d1): y=1/2x+b
=>y'=1/2
=>(x+1)^2=4
=>x=1 hoặc x=-3
Khi x=1 thì f(1)=0
y-f(1)=f'(1)(x-1)
=>y-0=1/2(x-1)=1/2x-1/2
Khi x=-3 thì f(-3)=(-4)/(-2)=2
y-f(-3)=f'(-3)(x+3)
=>y-2=1/2(x+3)
=>y=1/2x+3/2+2=1/2x+7/2
Đúng 0
Bình luận (0)
a) viết phương trình đường tròn (C) có tâm I(2,3) đi qua điểm A(5,7) b) viết phương trình tiếp tuyến của đường tròn (C) : (x-1)^2 + ( y+5)^2 =4 . Biết tiếp tuyến song song với đường thẳng (d) 3x + 4y - 1 =0
a) Để tìm phương trình đường tròn © có tâm I(2,3) đi qua điểm A(5,7), ta sử dụng công thức khoảng cách từ điểm đến tâm đường tròn:
$I\hat{A} = \sqrt{(x_A - x_I)^2 + (y_A - y_I)^2}$
Với I là tâm đường tròn, A là điểm trên đường tròn.
Ta có: $x_I = 2$, $y_I = 3$, $x_A = 5$, $y_A = 7$
Thay vào công thức ta được:
$\sqrt{(5-2)^2 + (7-3)^2} = \sqrt{34}$
Vậy bán kính của đường tròn là $\sqrt{34}$.
Phương trình đường tròn © có tâm I(2,3) và bán kính $\sqrt{34}$ là:
$(x-2)^2 + (y-3)^2 = 34$
b) Để tìm phương trình tiếp tuyến của đường tròn © : $(x-1)^2 + ( y+5)^2 =4$, ta cần tìm đạo hàm của phương trình đường tròn tại điểm cần tìm tiếp tuyến.
Ta có phương trình đường tròn chính giữa:
$(x-1)^2 + (y+5)^2 = 2^2$
Đạo hàm hai vế theo x:
$2(x-1) + 2(y+5)y' = 0$
Suy ra:
$y' = -\frac{x-1}{y+5}$
Tại điểm M(x,y) trên đường tròn, ta có:
$(x-1)^2 + (y+5)^2 = 2^2$
Đạo hàm hai vế theo x:
$2(x-1) + 2(y+5)y' = 0$
Suy ra:
$y' = -\frac{x-1}{y+5}$
Vậy tại điểm M(x,y), phương trình tiếp tuyến của đường tròn là:
$y - y_M = y'(x-x_M)$
Thay $y'$ bằng $\frac{-(x-1)}{y+5}$ và $x_M$, $y_M$ bằng 1, -5 ta được:
$y + 5 = \frac{-(x-1)}{y+5}(x-1)$
Simplifying:
$x(y+5) + y(x-1) = 6$
Đường thẳng (d) có phương trình là $3x + 4y - 1 = 0$. Vì tiếp tuyến song song với đường thẳng (d) nên hệ số góc của tiếp tuyến
Đúng 2
Bình luận (1)
Cho hàm số (C) : y= f(x) = \(\frac{X^3}{3}\) - 2x2 + 3x + 1. Viết phương trình tiếp tuyến của (C)
a) Biết tiếp tuyến vuông góc với d : y = x + 2
b) Biết tiếp tuyến song song với d : y = 3x + 2020
\(y'=x^2-4x+3\)
a/ Tiếp tuyến vuông góc với \(y=x+2\Rightarrow\) tiếp tuyến có hệ số góc k=-1
\(\Rightarrow x_0^2-4x_0+3=-1\)
\(\Leftrightarrow x_0^2-4x_0+4=0\Rightarrow x_0=2\)
\(\Rightarrow y\left(0\right)=\frac{5}{3}\)
Pt tiếp tuyến: \(y=-1\left(x-2\right)+\frac{5}{3}\Leftrightarrow y=-x+\frac{11}{3}\)
b/ Tiếp tuyến song song \(y=3x+2020\Rightarrow\) có hệ số góc \(k=3\)
\(\Leftrightarrow x_0^2-4x_0+3=3\Rightarrow\left[{}\begin{matrix}x_0=0\Rightarrow y_0=1\\x_0=4\Rightarrow y_0=\frac{7}{3}\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}y=3x+1\\y=3\left(x-4\right)+\frac{7}{3}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Phương trình tiếp tuyến của đồ thị hàm số
y
2
x
+
1
x
−
1
, biết tiếp tuyến song song với đường thẳng
d
:
y
−
3
x
−
1
A.
y
−...
Đọc tiếp
Phương trình tiếp tuyến của đồ thị hàm số y = 2 x + 1 x − 1 , biết tiếp tuyến song song với đường thẳng d : y = − 3 x − 1
A. y = − 3 x + 11 y = − 3 x − 1
B. y = − 3 x + 11
C. y = − 3 x + 1
D. y = − 3 x + 101 y = − 3 x − 1001
Đáp án B
Phương trình tiếp tuyến tại x 0 ; y 0 có hệ số góc là k = y ' = − 3 x − 1 2
Để tiếp tuyến tại x 0 ; y 0 song song với đường thẳng d : y = − 3 x − 1 thì
k = − 3 x − 1 2 = − 3 ⇔ x − 1 2 = 1 ⇔ x 1 = 2 x 2 = 0 ⇔ y 1 = 5 y 2 = − 1 ⇔ d 1 : y = − 3 x + 11 d 2 : y = − 3 x − 1 ≡ d ( l o a i )
Đúng 0
Bình luận (0)
y=\(x^3\)+\(x^2\)+3 viết phương trình tiếp tuyến của hàm số biết tiếp tuyến song song vs d: y=8x+9
Gọi `M(x,y)` là điểm thuộc TT.
`y'=3x^2+2x`
TT song song với `y=8x+9=> f'(x_0)=8`
`=> 3x_0^2+2x_0=8`
`<=>` \(\left[{}\begin{matrix}x_0=\dfrac{4}{3}\\x_0=-2\end{matrix}\right.\)
TH1: `x_0=4/3 => y_0 = 193/27`
`=>` PTTT: `y=8(x-4/3)+193/27=8x-96/27`
TH2: `x_0=-2 => y_0=-1`
`=>` PTTT: `y=8(x+2)-1=8x+15`
Đúng 1
Bình luận (0)
Cho hàm số
y
1
3
x
3
-
2
x
2
+
3
x
+
1
(C). Tìm phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến đó song song với đường thẳng
y
3
x
-
1
A.
y
3
x
+
1
B.
y
...
Đọc tiếp
Cho hàm số y = 1 3 x 3 - 2 x 2 + 3 x + 1 (C). Tìm phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến đó song song với đường thẳng y = 3 x - 1
A. y = 3 x + 1
B. y = 3 x - 29 3
C. y = 3 x + 20
D. Cả A và B đúng
Ta có y ' = x 2 - 4 x + 3 . Tiếp tuyến của đồ thị (C) song song với đường thẳng y = 3x - 1 nên hệ số góc của tiếp tuyến là k = 3.
Xét y' = 3 <=> x 2 - 4 x = 0
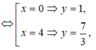
Phương trình tiếp tuyến của đồ thị tại A(0;1) có hệ số góc k = 3 là y = 3x + 1
Phương trình tiếp tuyến của đồ thị tại B(4; 7/3) có hệ số góc k = 3 là
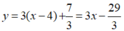
Chọn đáp án D.
Đúng 0
Bình luận (0)
Cho hàm số y = x - 1 x + 1 . Viết phương trình tiếp tuyến của đồ thị hàm số biết tiếp tuyến song song với d : y = x - 2 2
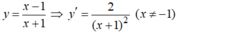
d: 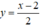 có hệ số góc k = 1/2 ⇒ Tiếp tuyến có hệ số góc k = 1/2.
có hệ số góc k = 1/2 ⇒ Tiếp tuyến có hệ số góc k = 1/2.
- Gọi ( x 0 , y 0 ) là toạ độ của tiếp điểm.
- Ta có:
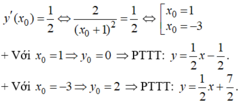
Đúng 0
Bình luận (0)
viết phương trình tiếp tuyến của hàm số y= x - 2 + 4/x - 1 biết tiếp tuyến song song với đường thẳng y= -3x + 1
y=x-2+\(\frac{x}{4}\)-1
\(\Leftrightarrow\)y=\(\frac{5x}{4}\)-3
\(\Rightarrow\)y'=(\(\frac{5x}{4}\)-3)'
\(\Rightarrow\)y'=(\(\frac{5x}{4}\))'-3'
\(\Rightarrow\)y'=\(\frac{\left(5x\right)'\cdot4-5x\cdot4'}{4_{ }^2}\)
\(\Rightarrow\)y'=\(\frac{20}{16}\)=\(\frac{5}{4}\)
Vì tiếp tuyến song song với đường thẳng y=-3x+1 nên:
f\('\left(x_0\right)\)=y'=-3 nhưng trong trường hợp này thì y' là một hằng số nên f'\(\left(3\right)\)=\(\frac{5}{4}\)
\(\)\(y_0\)=\(\frac{5\cdot\frac{5}{4}}{4}-3\)
\(y_0\)=\(\frac{-23}{16}\)
Vậy điểm M(\(\frac{5}{4}\);\(\frac{-23}{16}\)) thuộc đường tiếp tuyến đã cho.
Ta có công thức đường tiếp tuyến là:
y=f\('\left(x_0\right)\)(x-\(x_0\))+\(y_0\)
\(\Rightarrow\)y=3(x-\(\frac{5}{4}\))+\(\frac{-23}{16}\)
\(\Rightarrow\)y=3x-\(\frac{83}{16}\)
Đúng 0
Bình luận (0)
\(y=x-2+\frac{4}{x-1}\Rightarrow y'=1-\frac{4}{\left(x-1\right)^2}\)
Gọi \(M\left(a;b\right)\) là điểm có tiếp tuyến song song với d
\(\Rightarrow y'\left(a\right)=-3\Leftrightarrow1-\frac{4}{\left(a-1\right)^2}=-3\)
\(\Leftrightarrow\left(a-1\right)^2=1\Rightarrow\left[{}\begin{matrix}a=0\Rightarrow b=-6\\a=2\Rightarrow b=4\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn:
\(\left[{}\begin{matrix}y=-3x-6\\y=-3\left(x-2\right)+4\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}y=-3x-6\\y=-3x+10\end{matrix}\right.\)
Đúng 0
Bình luận (2)




