Bài 5b: Tiếp tuyến của đồ thị hàm số
Tìm phương trình tiếp tuyến của y=2x+1/1-x biết tiếp tuyến vuông góc với d : x+3y-2=0
Tìm phương trình tiếp tuyến y= x-2/x+1 biết tiếp tuyến song song với d : y=3x-2
Lời giải:
Vì PTTT của $y=\frac{x-2}{x+1}$ tại điểm $x=x_0$ song song với $y=3x-2$ nên:
$y'(x_0)=3$
$\Leftrightarrow \frac{3}{(x_0+1)^2}=3$
$\Leftrightarrow x_0=0$ hoặc $x_0=-2$
PTTT cần tìm:
$y=3(x-0)+y(0)=3x+\frac{0-2}{0+1}=3x-2$
$y=3(x+2)+y(-2)=3(x+2)+\frac{-2-2}{-2+1}=3x+6+4=3x+10$
Đúng 0
Bình luận (0)
Tìm phương trình tiếp tuyến y=x3+3x2-4 tại điểm có hoành độ x0=1
Lời giải:
$y=x^3+3x^2-4$
$\Rightarrow y'=3x^2+6x$
$\Rightarrow y'(x_0)=3.1^2+6.1=9$
$y_0=1^3+3.1^2-4=0$
PTTT của đths tại điểm có hoành độ $x_0=1$ là:
$y=y'(x_0)(x-x_0)+y_0=9(x-1)+0=9x-9$
Đúng 0
Bình luận (0)
Cho hàm số y2x+2x−1y2x+2x-1 có đồ thị là (C). Viết phương trình tiếp tuyến của (C), biết tiếp tuyến tạo với hai tiệm cận một tam giác có chu vi nhỏ nhất.A. Δ: y−x−1 ∆: y-x-1 và Δ: y−x+7∆: y-x+7B. Δ: y−x−3∆: y-x-3 và Δ: y−x+2∆: y-x+2C. Δ: y−x−1∆: y-x-1và Δ: y−x+17∆: y-x+17D. Δ: y−x−21∆: y-x-21và Δ: y−x+7
Đọc tiếp
Cho hàm số có đồ thị là (C). Viết phương trình tiếp tuyến của (C), biết tiếp tuyến tạo với hai tiệm cận một tam giác có chu vi nhỏ nhất.
A. và
B. và
C. và
D. và
ĐTHS có 2 tiệm cận là \(x=1\) và \(y=2\) \(\Rightarrow\) giao điểm 2 tiệm cận là \(I\left(1;2\right)\)
\(y'=\dfrac{-4}{\left(x-1\right)^2}\)
Gọi \(a\) là hoành độ tiếp điểm \(\Rightarrow\) pttt tại điểm có hoành độ bằng a có dạng:
\(y=-\dfrac{4}{\left(a-1\right)^2}\left(x-a\right)+\dfrac{2a+2}{a-1}\) (1)
Giao điểm với TCĐ: \(x=1\Rightarrow y=\dfrac{2a+6}{a-1}\) \(\Rightarrow A\left(1;\dfrac{2a+6}{a-1}\right)\)
\(\Rightarrow IA=\sqrt{\left(\dfrac{2a+6}{a-1}-2\right)^2}=\dfrac{8}{\left|a-1\right|}\)
Giao điểm với TCN: \(y=2\Rightarrow x=2a-1\) \(\Rightarrow B\left(2a-1;2\right)\)
\(\Rightarrow IB=\sqrt{\left(2a-1-1\right)^2}=2\left|a-1\right|\)
\(\Rightarrow\) Chu vi tam giác:
\(IA+IB+AB=IA+IB+\sqrt{IA^2+IB^2}\ge2\sqrt{IA.IB}+\sqrt{2IA.IB}=8+4\sqrt{2}\)
Dấu "=" xảy ra khi:
\(\dfrac{8}{\left|a-1\right|}=2\left|a-1\right|\Rightarrow\left(a-1\right)^2=4\Rightarrow\left[{}\begin{matrix}a=3\\a=-1\end{matrix}\right.\)
Thay vào (1)\(\Rightarrow y=-x-1\) và \(y=-x+7\)
Đúng 0
Bình luận (0)
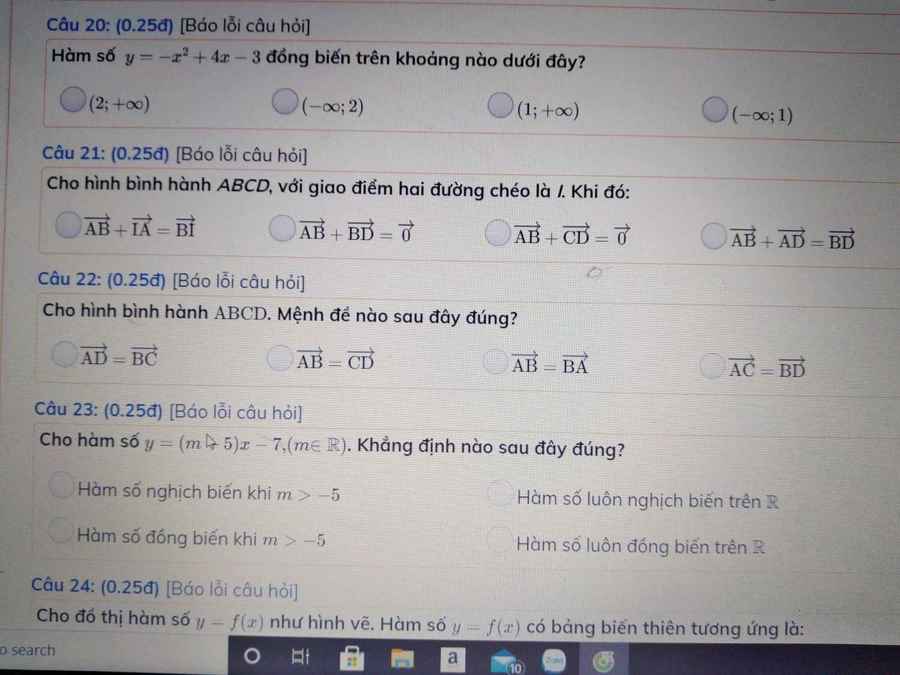
20/ \(y'=-2x+4>0\Leftrightarrow x< 2\Rightarrow x\in\left(-\infty;2\right)\)
21/\(\left\{{}\begin{matrix}AB=CD\\\overrightarrow{AB}\uparrow\downarrow\overrightarrow{CD}\end{matrix}\right.\Rightarrow\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{0}\)
23/\(y'=m+5;\left\{{}\begin{matrix}y'>0\Leftrightarrow m>-5\\y'< 0\Leftrightarrow m< -5\end{matrix}\right.\Rightarrow A\)
Đúng 0
Bình luận (0)
cho phương trình -x2+2x+4\(\sqrt{ }\)-x2+2x+3=m-2 tìm m để pt có nghiệm
Câu này giải có bbt như thế nào vậy?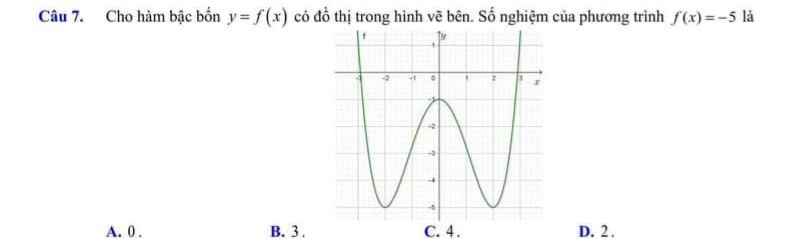
D. 2
Kẻ đường thẳng `y=f(x)=5` -> Số giao điểm = số nghiệm.
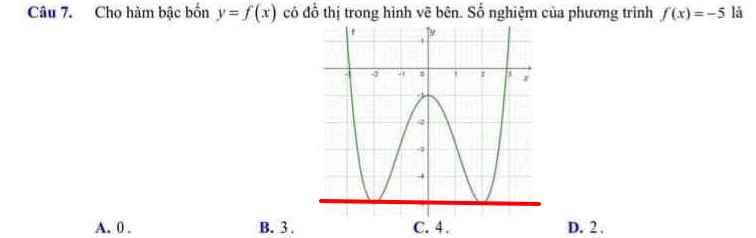
Đúng 1
Bình luận (1)
cho hàm số \(y=\dfrac{2x-1}{x+1}\) có đồ thị (C). Viết phương trình tiếp tuyến của (C) biết rằng tiếp tuyến đó cách điểm A(0;1) một khoảng bằng 1
\(y'=\dfrac{3}{\left(x+1\right)^2}\)
Gọi \(M\left(m;\dfrac{2m-1}{m+1}\right)\) là tiếp điểm
Phương trình tiếp tuyến tại M:
\(y=\dfrac{3}{\left(m+1\right)^2}\left(x-m\right)+\dfrac{2m-1}{m+1}\)
\(\Leftrightarrow3x-\left(m+1\right)^2y+2m^2-2m-1=0\)
Áp dụng công thức khoảng cách:
\(\dfrac{\left|-\left(m+1\right)^2+2m^2-2m-1\right|}{\sqrt{9+\left(m+1\right)^4}}=1\)
Bạn tự giải ra m nhé
Đúng 2
Bình luận (0)
Phương trình tiếp tuyến của đồ thị hàm số y=\(x^3-3x+4\) tại giao điểm với trục tung.