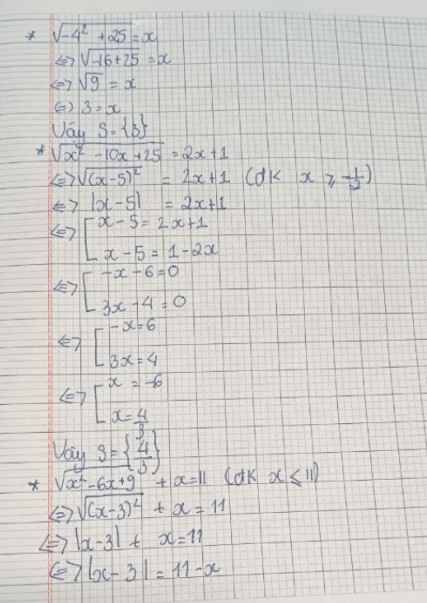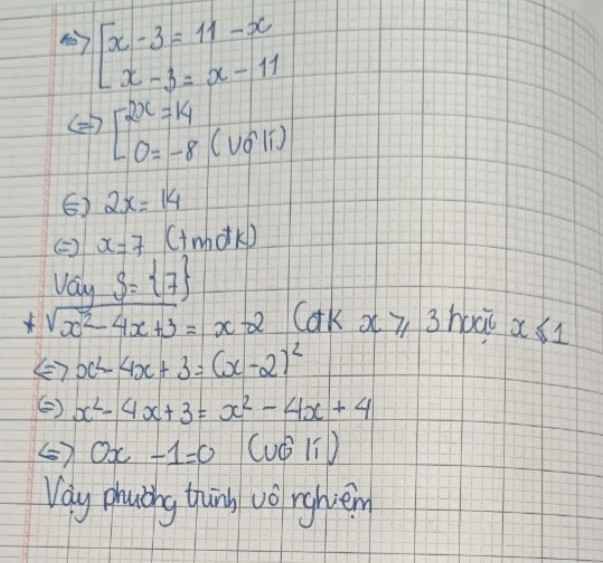Thiếu soát gì mog bạn thông cảm :]

1, \(\sqrt{4-4x+x^2}=3\)

\(\Leftrightarrow\sqrt{\left(2+x\right)^2}=3\)

\(\Leftrightarrow\left|2+x\right|=3\)

TH1: \(\left|2-x\right|=2-x\) với \(2-x\ge0\Leftrightarrow x\le2\)

Pt trở thành:

\(2-x=3\) (ĐK: \(x\le2\) )

\(\Leftrightarrow x=2-3\)

\(\Leftrightarrow x=-1\left(tm\right)\)

TH2: \(\left|2-x\right|=-\left(2-x\right)\) với \(2-x< 0\Leftrightarrow x>2\)

Pt trở thành:

\(-\left(2-x\right)=3\) (ĐK: \(x>2\))

\(\Leftrightarrow-2+x=3\)

\(\Leftrightarrow x=3+2\)

\(\Leftrightarrow x=5\left(tm\right)\)

Vậy \(S=\left\{-1;5\right\}\)

2, \(\sqrt{x^2-6x+9}=1\)

\(\Leftrightarrow\sqrt{x^2-2\cdot3\cdot x+3^2}=1\)

\(\Leftrightarrow\sqrt{\left(x-3\right)^2}=1\)

\(\Leftrightarrow\left|x-3\right|=1\)

TH1: \(\left|x-3\right|=x-3\) với \(x-3\ge0\Leftrightarrow x\ge3\)

Pt trở thành:

\(x-3=1\) (ĐK: \(x\ge3\))

\(\Leftrightarrow x=1+3\)

\(\Leftrightarrow x=4\left(tm\right)\)

TH2: \(\left|x-3\right|=-\left(x-3\right)\) với \(x-3< 0\Leftrightarrow x< 3\)

Pt trở thành:

\(-\left(x-3\right)=1\) (ĐK: \(x< 3\))

\(\Leftrightarrow-x+3=1\)

\(\Leftrightarrow-x=1-3\)

\(\Leftrightarrow-x=-2\)

\(\Leftrightarrow x=2\left(tm\right)\)

Vậy \(S=\left\{2;4\right\}\)

1) √(4 - 4x + x²) = 3

⇔ √(2 - x)² = 3

ĐKXĐ: Với mọi x ∈ R

⇔ |2 - x| = 3 (1)

*) |2 - x| = 2 - x ⇔ 2 - x ≥ 0 ⇔ x ≥ 2

(1) ⇔ 2 - x = 3

⇔ x = 2 - 3

⇔ x = -1 (nhận)

*) |2 - x| = x - 2 ⇔ 2 - x < 0 ⇔ x > 2

(1) ⇔ x - 2 = 3

⇔ x = 5 (nhận)

Vậy x = -1; x = 5

\(M=\sqrt{x^2-4x+4}+2014\sqrt{x^2-6x+9}+\sqrt{x^2-10x+25}\)

\(M=\left|x-2\right|+2014\left|x-3\right|+\left|x-5\right|\)

\(M=\left|x-2\right|+\left|5-x\right|+2014\left|x-3\right|\)

\(M\ge\left|x-2+5-x\right|+2014\left|x-3\right|=3+2014\left|x-3\right|\ge3\)

\("="\Leftrightarrow x=3\)

Em biết làm mỗi ý đầu thôi ạ :(

\(\sqrt{9x^2-6x+1}=4\)

\(\Leftrightarrow\sqrt{\left(3x-1\right)^2}=4\)

\(\Leftrightarrow\left|3x-1\right|=4\)

\(\Leftrightarrow\orbr{\begin{cases}3x-1=4\\3x-1=-4\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\frac{5}{3}\\x=-1\end{cases}}\)

Vậy S = { 5/3 ; -1 }

bạn kiểm tra lại đề bài câu (b) nhé! mình nghĩ là \(\sqrt{x^2+10x+25}=x+4\) chuẩn hơn

\(\sqrt{x^2+10x+25}=x+4\)

\(\Leftrightarrow\sqrt{\left(x+5\right)^2}=x+4\)

\(\Leftrightarrow x+5=x+4\)( mâu thuẩn )

\(\sqrt{9x^2-6x+1}=4\)

\(\Leftrightarrow\sqrt{\left(3x-1\right)^2}=4\)

\(\Leftrightarrow3x-1=4\Leftrightarrow x=\frac{5}{3}\)

a) \(\Leftrightarrow\sqrt{\left(x+3\right)^2}=4\)

\(\Leftrightarrow\left|x+3\right|=4\) \(\Leftrightarrow\left[{}\begin{matrix}x+3=4\\x+3=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-7\end{matrix}\right.\) ( TM )

b) \(\Leftrightarrow\sqrt{\left(2x-1\right)^2}=5x+3\)

\(\Leftrightarrow\left|2x-1\right|=5x+3\)

\(\Leftrightarrow\left\{{}\begin{matrix}5x+3\ge0\\\left[{}\begin{matrix}2x-1=5x+3\\2x-1=-5x-3\end{matrix}\right.\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-\frac{3}{5}\\\left[{}\begin{matrix}x=-\frac{4}{3}\left(KTM\right)\\x=-\frac{2}{7}\left(TM\right)\end{matrix}\right.\end{matrix}\right.\)

a \(\sqrt{x^2+6x+9}=4\Leftrightarrow\sqrt{\left(x+3\right)^2=4}\)

\(\Leftrightarrow x+3=4\)

\(\Rightarrow x=1\)

a) \(\sqrt{x^2-10x+25}+\sqrt{x^2-6x+9}=\sqrt{\left(x-5\right)^2}+\sqrt{\left(x-3\right)^2}=\left|x-5\right|+\left|x-3\right|\)

Vì x > 5 nên x - 5 > 0 , x - 3 > 0

=> \(\left|x-5\right|+\left|x-3\right|=x-5+x-3=2x-8\)

b) Điều kiện phải là \(2\le x< 3\)

 \(\sqrt{x^2-6x+9}-\sqrt{x^2-4x+4}=\sqrt{\left(x-3\right)^2}-\sqrt{\left(x-2\right)^2}=\left|x-3\right|-\left|x-2\right|\)

Vì \(2\le x< 3\Rightarrow\hept{\begin{cases}x-2\ge0\\x-3< 0\end{cases}}\)

=> \(\left|x-3\right|-\left|x-2\right|=3-x-\left(x-2\right)=-2x+5\)

a)\(\sqrt{3x+2}=2-\sqrt{3}\)

\(\Leftrightarrow3x+2=\left(2-\sqrt{3}\right)^2\)

\(\Leftrightarrow3x+2=7-4\sqrt{3}\)

\(\Leftrightarrow3x=7-2-4\sqrt{3}\)

\(\Leftrightarrow3x=5-4\sqrt{3}\)

\(\Leftrightarrow x=\dfrac{5}{3}-\dfrac{4\sqrt{3}}{3}\)

\(\Leftrightarrow x=\dfrac{5-4\sqrt{3}}{3}\)

b) \(\sqrt{x^2-4x+4}=49\)

\(\Leftrightarrow\sqrt{\left(x-2\right)^2}=49\)

\(\Leftrightarrow\left|x-2\right|=49\)\

\(\Leftrightarrow\left[{}\begin{matrix}x-2=49\\-x+2=49\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=51\\x=-47\end{matrix}\right.\)

c) \(\sqrt{x+1}=x-1\)

ĐKXĐ: \(x-1\ge0\Rightarrow x\ge1\)

\(\Leftrightarrow x+1=\left(x-1\right)^2\)

\(\Leftrightarrow x+1=x^2-2x+1\)

\(\Leftrightarrow-x^2+2x+x=-1+1\)

\(\Leftrightarrow3x-x^2=0\)

\(\Leftrightarrow x\left(3-x\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\3-x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(lo\text{ại}\right)\\x=3\left(nh\text{ậ}n\right)\end{matrix}\right.\)

d)e) lát mình làm sau

26: \(x^2-\sqrt{x}+x-1\)

\(=\sqrt{x}\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)+\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)\)

\(=\left(\sqrt{x}-1\right)\left(x\sqrt{x}+x+\sqrt{x}+\sqrt{x}+1\right)\)

\(=\left(\sqrt{x}-1\right)\left(x\sqrt{x}+x+2\sqrt{x}+1\right)\)

25: Ta có: \(-6x+7\sqrt{x}-2\)

\(=-6x+3\sqrt{x}+4\sqrt{x}-2\)

\(=-3\sqrt{x}\left(2\sqrt{x}-1\right)+2\left(2\sqrt{x}-1\right)\)

\(=\left(2\sqrt{x}-1\right)\left(2-3\sqrt{x}\right)\)

27: Ta có: \(2a-5\sqrt{ab}+3b\)

\(=2a-2\sqrt{ab}-3\sqrt{ab}+3b\)

\(=2\sqrt{a}\left(\sqrt{a}-\sqrt{b}\right)-3\sqrt{b}\left(\sqrt{a}-\sqrt{b}\right)\)

\(=\left(\sqrt{a}-\sqrt{b}\right)\left(2\sqrt{a}-3\sqrt{b}\right)\)

28: Ta có: \(\sqrt{ab}+2\sqrt{a}+3\sqrt{b}+6\)

\(=\sqrt{a}\left(\sqrt{b}+2\right)+3\left(\sqrt{b}+2\right)\)

\(=\left(\sqrt{b}+2\right)\left(\sqrt{a}+3\right)\)