Cho hàm số y=1/4x^2 Tìm hoành độ giao điểm của M thuộc đồ thị (P) biết M có tung độ bằng 25
ND
Những câu hỏi liên quan
Cho hàm số y= 1/4x^2 có đồ thị là (P)
a) Vẽ đồ thị (P) trên mặt phẳng tọa độ Oxy
b) Tìm hoành độ của điểm M thuộc đồ thị (P) biết M có tung độ bằng 100
a) Bảng giá trị:

Đồ thị:
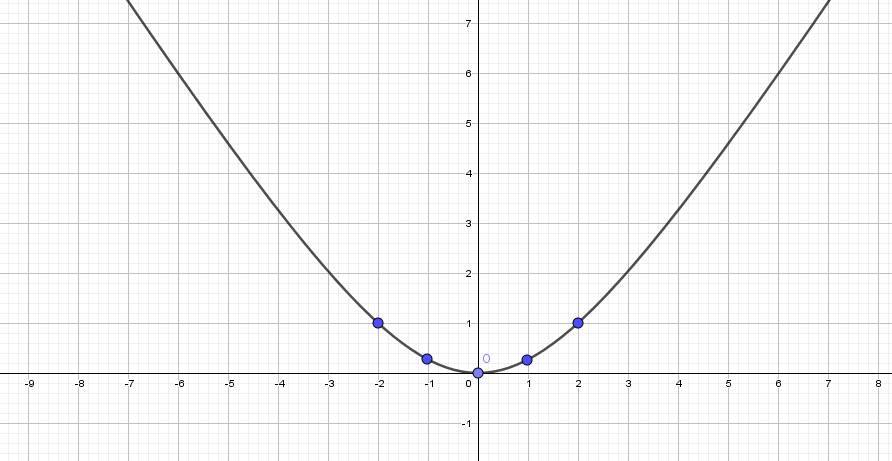
b) Thay y = 100 vào (P) ta được:
\(\dfrac{1}{4}x^2=100\)
\(\Leftrightarrow x^2=100:\dfrac{1}{4}\)
\(\Leftrightarrow x^2=400\)
\(\Leftrightarrow\left[{}\begin{matrix}x=20\\x=-20\end{matrix}\right.\)
Vậy M(-20; 100) hoặc M(20; 100)
Đúng 1
Bình luận (0)
b: y=100
=>1/4x^2=100
=>x^2=400
=>x=20 hoặc x=-20
a: 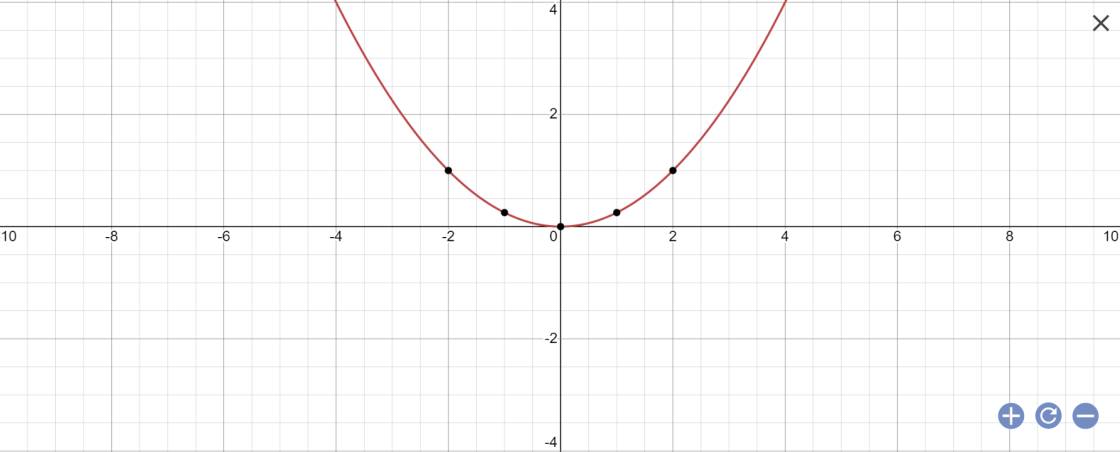
Đúng 0
Bình luận (0)
a.Trong các điểm sau đây, điểm nào thuộc đồ thị của hàm số (1)? Vì sao? B(-1; 2) ; C(- 2 ;- 4) b.Vẽ đồ thị của hàm số đó c.Tìm tung độ của điểm M biết M thuộc đồ thị của hàm số (1) có hoành độ bằng 3. d. Tìm hoành độ của các điểm thuộc đồ thị của hàm số (1) biết tung độ của chúng bằng 3.
giúp mik vs ạ mik dag cần gấp ạ
Cho hàm y=ax. Biết x=-3 thì y=2
a) Xác định hàm số đó. Vẽ đồ thị của hàm số đó
b) Biết điểm B thuộc đồ thị có hoành độ là 3, tìm tung độ của B
c) C thuộc đồ thị có tung độ là -4. Tìm hoành độ của C
d) Điểm M(4;-3) ; N(2;-4/3) điểm nào thuộc đồ thị hàm số
Cho hàm số y=(m-1)x+m
a) Xác định m để đồ thị hàm số cắt trục tung điểm có tung độ bằng 3, cắt trục hoành tại điểm có hoành độ bằng 3
b) Vẽ đồ thị hàm số của hai hàm số ứng với m tìm được câu a
c) Gọi giao điểm của 2 đồ thị với trục hoành lần lượt là A;B giao điểm của 2 đồi thị là C. Tính chu vi và diện tích của tam giác ABC
Trước hết xin nói ngay rằng đồ thị của hàm số y = (2x - 1)(x - 1) là một parabol, không có đường tiệm cận nào cả.
Có lẽ bạn muốn nói đến hàm số y = (2x - 1)/(x - 1).
Nếu đúng vậy thì đồ thị của hàm số là một hyperbol vuông góc có hai đường tiệm cận là đường thẳng x = 1 và đường thẳng y = 2.
Giao điểm của hai đường tiệm cận là I(1; 2).
Gọi M(x,y) là một điểm trên đồ thị. Hệ số góc của đường thẳng IM là
m = (y - 2)/(x - 1) = {[(2x - 1)/(x - 1)] - 2}/(x - 1) = [(2x - 1) - 2(x - 1)]/(x - 1)²
m = 1/(x - 1)²
Hệ số góc của đường tiếp tuyến Mt với đồ thị tại M(x,y) là
m' = dy/dx = -1/(x - 1)²
Muốn cho MI và Mt thẳng góc với nhau thì điều kiện cần và đủ là
mm' = -1
-1/(x - 1)^4 = -1
(x - 1)^4 = 1
(x - 1)² = 1
x - 1 = ±1
x = 0 hay x = 2
Có 2 điểm M thỏa mãn điều kiện của bài toán là (0; 1) và (2; 3)
Đúng 0
Bình luận (0)
Bài 3. Cho hàm số y = (m-2)x + m
a) Tìm m để đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 2
b) Tìm m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng -3
c) Tìm m để đồ thị hàm số đi qua điểm A(1; 2)
a)Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 2
\(\Rightarrow2=\left(m-2\right).0+m\) \(\Leftrightarrow m=2\)
Vậy m=2 thì đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 2
b) Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng -3
\(\Rightarrow0=\left(m-2\right)\left(-3\right)+m\) \(\Leftrightarrow m=3\)
Vậy...
c) Hàm số đi qua điểm A(1;2)
\(\Rightarrow2=\left(m-2\right).1+m\)\(\Leftrightarrow m=2\)
Vậy...
Đúng 1
Bình luận (0)
a) Đồ thị cắt trục tung tại điểm có tung độ bằng 2
\(\Rightarrow\) điểm đó có tọa độ là \(\left(0;2\right)\)
\(\Rightarrow2=m\)
b) Đồ thị cắt trục hoành tại điểm có hoành độ bằng -3
\(\Rightarrow\) điểm đó có tọa độ là \(\left(-3;0\right)\)
\(\Rightarrow0=-3m+6+m=-2m+6\Rightarrow m=3\)
c) Đồ thị đi qua điểm \(A\left(1;2\right)\)
\(\Rightarrow2=m-2+m\Rightarrow m=2\)
Đúng 0
Bình luận (2)
Cho hàm số y=2x-3
a)Tìm tọa độ điểm A là giao điểm đồ thị với trục tung
b)Tìm tọa độ điểm B là giao điểm đồ thị với trục hoành
c)Tìm tọa độ điểm C thuộc đồ thị có hoành độ bằng 2
d)Tìm tọa độ điểm B thuộc đồ thị có tung độ bằng -15
Cho hàm số y=(m-1)x+m
a) Xác định m để đồ thij hàm số cắt trục tung điểm có tung độ bằng 3, cắt trục hoành tại điểm có tung độ bằng 3
b) Vẽ đồ thị hàm số của hai hàm số ứng với m tìm được câu a
c) Gọi giao điểm của 2 đồ thị với trục hoành lần lượt là A; B giao điiểm của hai đồ thị là C. Tính chu vi và diện tích của tam giác ABC
Trước hết xin nói ngay rằng đồ thị của hàm số y = (2x - 1)(x - 1) là một parabol, không có đường tiệm cận nào cả.
Có lẽ bạn muốn nói đến hàm số y = (2x - 1)/(x - 1).
Nếu đúng vậy thì đồ thị của hàm số là một hyperbol vuông góc có hai đường tiệm cận là đường thẳng x = 1 và đường thẳng y = 2.
Giao điểm của hai đường tiệm cận là I(1; 2).
Gọi M(x,y) là một điểm trên đồ thị. Hệ số góc của đường thẳng IM là
m = (y - 2)/(x - 1) = {[(2x - 1)/(x - 1)] - 2}/(x - 1) = [(2x - 1) - 2(x - 1)]/(x - 1)²
m = 1/(x - 1)²
Hệ số góc của đường tiếp tuyến Mt với đồ thị tại M(x,y) là
m' = dy/dx = -1/(x - 1)²
Muốn cho MI và Mt thẳng góc với nhau thì điều kiện cần và đủ là
mm' = -1
-1/(x - 1)^4 = -1
(x - 1)^4 = 1
(x - 1)² = 1
x - 1 = ±1
x = 0 hay x = 2
Có 2 điểm M thỏa mãn điều kiện của bài toán là (0; 1) và (2; 3)
Đúng 0
Bình luận (0)
2, Giao điểm của hai đường tiệm cận là I(1; 2).
Gọi M(x,y) là một điểm trên đồ thị. Hệ số góc của đường thẳng IM là
m = (y - 2)/(x - 1) = {[(2x - 1)/(x - 1)] - 2}/(x - 1) = [(2x - 1) - 2(x - 1)]/(x - 1)²
m = 1/(x - 1)²
Hệ số góc của đường tiếp tuyến Mt với đồ thị tại M(x,y) là
m' = dy/dx = -1/(x - 1)²
Muốn cho MI và Mt thẳng góc với nhau thì điều kiện cần và đủ là
mm' = -1
-1/(x - 1)^4 = -1
(x - 1)^4 = 1
(x - 1)² = 1
x - 1 = ±1
x = 0 hay x = 2
Có 2 điểm M thỏa mãn điều kiện của bài toán là (0; 1) và (2; 3)
Câu 2:1) Cho hàm số ydfrac{1}{4}x^2 có đồ thị (P). Vẽ đồ thị (P) trên mặt phẳng tọa độ Oxy2) Tìm hoành độ của điểm M thuộc đồ thị (P) biết M có tung độ bằng 25Câu 3:1) Tìm giá trị của tham số m để phương trình x2 - 2x + m 0 có hai nghiệm phân biệt2) Cho x1 và x2 là hai nghiệm của phương trình x2 - 2x - 1 03) Tính giá trị của biểu thức T (x1)2 + (x2)2
Đọc tiếp
Câu 2:
1) Cho hàm số \(y=\dfrac{1}{4}x^2\) có đồ thị (P). Vẽ đồ thị (P) trên mặt phẳng tọa độ Oxy
2) Tìm hoành độ của điểm M thuộc đồ thị (P) biết M có tung độ bằng 25
Câu 3:
1) Tìm giá trị của tham số m để phương trình x2 - 2x + m = 0 có hai nghiệm phân biệt
2) Cho x1 và x2 là hai nghiệm của phương trình x2 - 2x - 1 = 0
3) Tính giá trị của biểu thức T = (x1)2 + (x2)2
Câu 2:1) Cho hàm số ydfrac{1}{4}x^2 có đồ thị (P). Vẽ đồ thị (P) trên mặt phẳng tọa độ Oxy2) Tìm hoành độ của điểm M thuộc đồ thị (P) biết M có tung độ bằng 25Câu 3:1) Tìm giá trị của tham số m để phương trình x2 - 2x + m 0 có hai nghiệm phân biệt2) Cho x1 và x2 là hai nghiệm của phương trình x2 - 2x - 1 03) Tính giá trị của biểu thức T (x1)2 + (x2)2
Đọc tiếp
Câu 2:
1) Cho hàm số \(y=\dfrac{1}{4}x^2\) có đồ thị (P). Vẽ đồ thị (P) trên mặt phẳng tọa độ Oxy
2) Tìm hoành độ của điểm M thuộc đồ thị (P) biết M có tung độ bằng 25
Câu 3:
1) Tìm giá trị của tham số m để phương trình x2 - 2x + m = 0 có hai nghiệm phân biệt
2) Cho x1 và x2 là hai nghiệm của phương trình x2 - 2x - 1 = 0
3) Tính giá trị của biểu thức T = (x1)2 + (x2)2





