Bài 2: Hàm số bậc nhất.

Các anh/ chị giúp em với ạ!

a: 2x-3y=5

=>3y=2x-5

=>\(y=\dfrac{2}{3}x-\dfrac{5}{3}\)

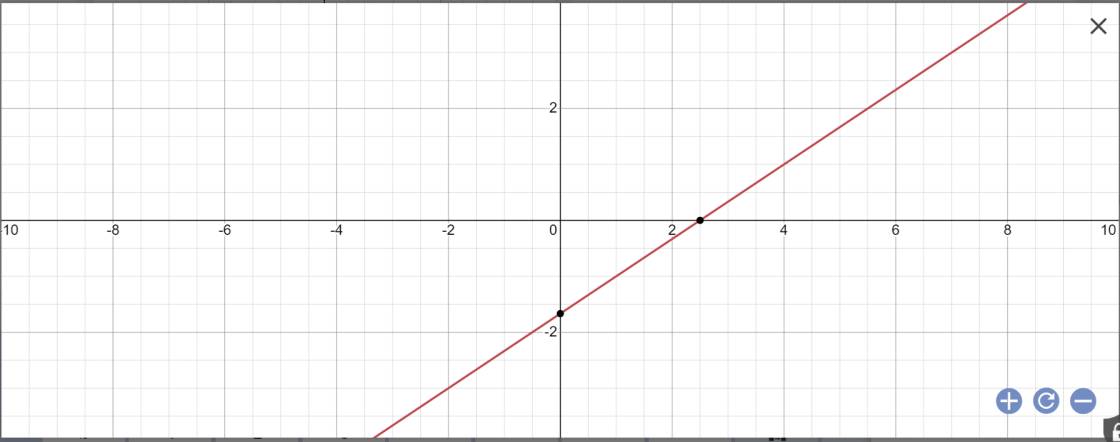
Vậy: Công thức nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=\dfrac{2}{3}x-\dfrac{5}{3}\end{matrix}\right.\)

Biểu diễn tập nghiệm:

b: 4x+0y=12

=>4x=12

=>x=3

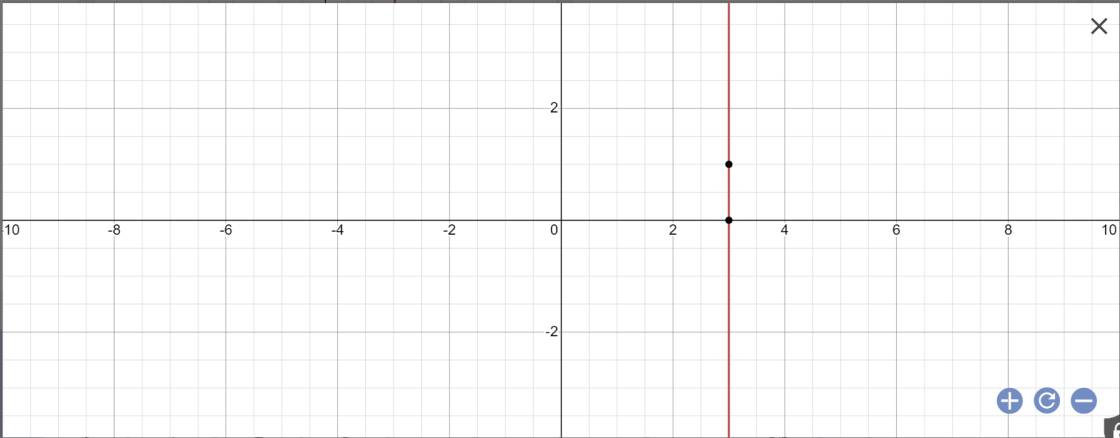
Vậy: Công thức nghiệm tổng quát là \(\left\{{}\begin{matrix}x=3\\y\in R\end{matrix}\right.\)

Biểu diễn tập nghiệm:

c: 0x-3y=6

=>-3y=6

=>y=-2

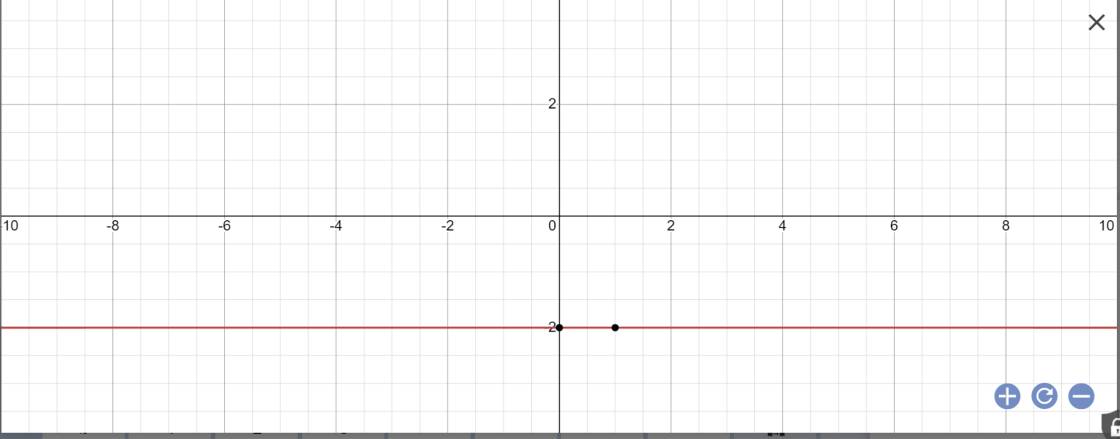
Vậy: Công thức nghiệm tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=-2\end{matrix}\right.\)

Biểu diễn tập nghiệm:

a: y=(m-2)x+2

=mx-2x+2

Tọa độ điểm mà D luôn đi qua là;

\(\left\{{}\begin{matrix}x=0\\y=-2x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=-2\cdot0+2=2\end{matrix}\right.\)

b: Đề sai rồi bạn

a: Phương trình hoành độ giao điểm là:

2x+4=-x+1

=>2x+x=1-4

=>3x=-3

=>x=-1

Thay x=-1 vào y=-x+1, ta được:

y=-(-1)+1=2

Vậy: A(-1;2)

b: A(-1;-2); B(-1;4); O(0;0)

\(OA=\sqrt{\left(-1-0\right)^2+\left(-2-0\right)^2}=\sqrt{1+4}=\sqrt{5}\)

\(OB=\sqrt{\left(-1-0\right)^2+4^2}=\sqrt{16+1}=\sqrt{17}\)

\(AB=\sqrt{\left(-1+1\right)^2+\left(4+2\right)^2}=6\)

Xét ΔOAB có \(cosAOB=\dfrac{OA^2+OB^2-AB^2}{2\cdot OA\cdot OB}=\dfrac{5+17-36}{2\cdot\sqrt{5}\cdot\sqrt{17}}=\dfrac{-7}{\sqrt{85}}\)

=>\(sinAOB=\sqrt{1-\left(-\dfrac{7}{\sqrt{85}}\right)^2}=\dfrac{6}{\sqrt{85}}\)

Diện tích tam giác OAB là:

\(S_{AOB}=\dfrac{1}{2}\cdot AO\cdot OB\cdot sinAOB\)

\(=\dfrac{1}{2}\cdot\dfrac{6}{\sqrt{85}}\cdot\sqrt{17}\cdot\sqrt{5}=3\)

a)

Ta thấy \(\sqrt{3}-2< 0\) nên hàm số trên nghịch biến trên R

b) 

\(\sqrt{3}-7=\left(\sqrt{3}-2\right)x+5\)

\(\Leftrightarrow\sqrt{3}-12=\left(\sqrt{3}-2\right)x\)

\(\Leftrightarrow x=\dfrac{\sqrt{3}-12}{\sqrt{3}-2}\)

Gọi (d): y=ax+b là phương trình hàm số bậc nhất cần tìm

Vì (d)//y=2x-1 nên a=2 và \(b\ne1\)

Vậy: (d): y=2x+b

Thay x=1 vào y=3x+2, ta được:

\(y=3\cdot1+2=3+2=5\)

Thay x=1 và y=5 vào (d), ta được:

\(b+2\cdot1=5\)

=>b+2=5

=>b=3

Vậy: (d): y=2x+3

Để hàm số y = ( 2m + 1 )x là hàm số bậc nhất

=> 2m + 1 ≠ 0

⇔ 2m ≠ -1

⇔ m ≠ \(\dfrac{-1}{2}\)

Để hàm số đã cho là hàm số bậc nhất thì:

2m + 1 ≠ 0

⇔ 2m ≠ -1

⇔ m ≠ -1/2

a: Để hàm số y=kx-3 đồng biến trên R thì k>0

b: Để hàm số y=2kx+1 đồng biến trên R thì 2k>0

=>k>0

c: Để hàm số \(y=\left(4k+2\right)x+1\) đồng biến trên R thì 4k+2>0

=>4k>-2

=>\(k>-\dfrac{1}{2}\)

Để hàm số đồng biến trên R thì:

a) k > 0

b) 2k > 0

⇔ k > 0

c) 4k + 2 > 0

⇔ 4k > -2

⇔ k > -1/2

Lời giải:
a. Để $y=mx+3$ là hàm bậc nhất thì \(\left\{\begin{matrix} m\in\mathbb{R}\\ m\neq 0\end{matrix}\right.\)

b. Để $y=2mx-1$ là hàm bậc nhất thì \(\left\{\begin{matrix} 2m\in\mathbb{R}\\ 2m\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m\in\mathbb{R}\\ m\neq 0\end{matrix}\right.\)

Ta có:

f(5) = 5a + b

f(4) = 4a + b

⇒ f(5) - f(4) = 5a + b - (4a + b)

= 5a + b - 4a - b

= a > 0

Vậy f(5) > f(4)