Chương IV - Hàm số y = ax^2 (a khác 0). Phương trình bậc hai một ẩn

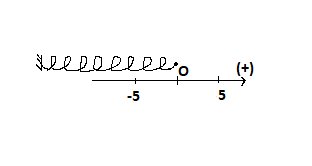
- Chiều dài cực đại của lò xò trong quá trình vật dao động chính là chiều dài của lò xo tới li độ \(x=5cm\):         \(20+5=25\left(cm\right)\) 
- Chiều dài cực tiểu của lò xò trong quá trình vật dao động chính là chiều của lò xo tới li độ \(x=-5cm\):           \(20-5=15\left(cm\right)\)    
                Vậy.....

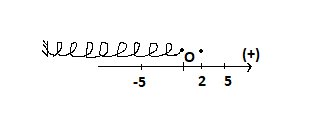
Ta có chiều dài lò xo tại vị trí cân bằng chính là chính là chiều dài tự nhiên của lò xo nên chiều dài lò xo tại vị trí cân bằng là: \(20cm\)
Chiều dài của lò xo tại vị trí có li độ \(x=2cm\) là: \(20+2=22\left(cm\right)\)
Vậy chiều dài của lò xo tại vị trí có li độ\(x=2cm\) là \(22cm\)

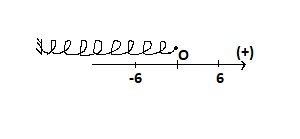
Vị trí ban đầu của con lắc lò xo chính là vị trí cân bằng, nên chiều dài tự nhiên của lò xo chính là chiều dài của con lắc lò xo ở vị trí cân bằng.
Như vậy chiều dài của con lắc lò xo ở vị trí cân bằng là 20cm.

a)

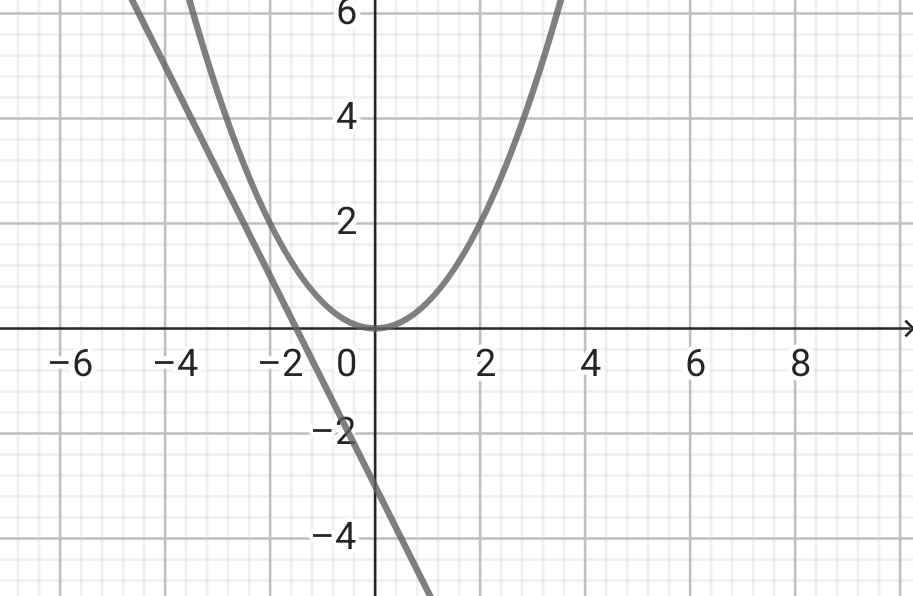
b) Phương trình hoành độ giao điểm của (P) và (d):

x²/2 = -2x - 3

x² = -4x - 6

x² + 4x + 6 = 0

Do x² + 4x + 6 = x² + 4x + 4 + 2

= (x + 2)² + 2 > 0 với mọi x ∈ R

⇒ (P) và (d) không giao nhau

c) Do (P) và (d) không giao nhau nên không tính được theo yêu cầu đề bài

a: \(x^2-2\left(2m-1\right)x+4m-8=0\)

\(\Delta=\left[-2\left(2m-1\right)\right]^2-4\cdot1\left(4m-8\right)\)

\(=4\left(4m^2-4m+1\right)-4\left(4m-8\right)\)

\(=16m^2-16m+4-16m+32\)

\(=16m^2-32m+36\)

\(=16m^2-32m+16+20=\left(4m-4\right)^2+20>=20>0\forall m\)

=>Phương trình luôn có hai nghiệm phân biệt

b: 

\(x^2-\left(m+1\right)x+m-1=0\)

\(\Delta=\left[-\left(m+1\right)\right]^2-4\cdot1\left(m-1\right)\)

\(=\left(m+1\right)^2-4\left(m-1\right)\)

\(=m^2+2m+1-4m+4=m^2-2m+5\)

\(=\left(m-1\right)^2+4>=4>0\forall m\)

=>Phương trình luôn có hai nghiệm phân biệt

c:\(x^2-2\left(m-1\right)x+m-3=0\)

 \(\Delta=\left[-2\left(m-1\right)\right]^2-4\cdot1\left(m-3\right)\)

\(=4\left(m-1\right)^2-4\left(m-3\right)\)

\(=4m^2-8m+4-4m+12\)

\(=4m^2-12m+16=4m^2-12m+9+7\)

\(=\left(2m-3\right)^2+7>=7>0\forall m\)

=>Phương trình luôn có hai nghiệm phân biệt

d: \(x^2+\left(m+3\right)x+m+1=0\)

\(\Delta=\left(m+3\right)^2-4\cdot1\left(m+1\right)\)

\(=m^2+6m+9-4m-4\)

\(=m^2-2m+5=\left(m-1\right)^2+4>=4>0\forall m\)

=>Phương trình luôn có hai nghiệm phân biệt

Bài 5:

a: Thay x=1 vào (P), ta được:

\(y=-1^2=-1\ne-2=y_M\)

Vậy: M(1;-2) không thuộc (P)

b: Phương trình hoành độ giao điểm là:

\(-x^2=\left(m-2\right)x-m\)

=>\(x^2+\left(m-2\right)x-m=0\)

\(\text{Δ}=\left(m-2\right)^2-4\cdot1\cdot\left(-m\right)\)

\(=m^2-4m+4+4m=m^2+4>0\)

=>(P) luôn cắt (d) tại hai điểm phân biệt

Theo Vi-et, ta được:

\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-\left(m-2\right)\\x_1x_2=\dfrac{c}{a}=-m\end{matrix}\right.\)

\(x_1^2-x_1+x_2^2-x_2=2\)

=>\(\left(x_1^2+x_2^2\right)-\left(x_1+x_2\right)=2\)

=>\(\left(x_1+x_2\right)^2-2x_1x_2-\left(x_1+x_2\right)=2\)

=>\(\left(m-2\right)^2-2\left(-m\right)-\left(-m+2\right)=2\)

=>\(m^2-4m+4+2m+m-2=2\)

=>\(m^2-m=0\)

=>m(m-1)=0

=>\(\left[{}\begin{matrix}m=0\\m=1\end{matrix}\right.\)

Bài 4:

a: Thay x=1 và y=-2 vào (d), ta được:

\(m\cdot1-m+1=-2\)

=>1=-2(vô lý)

=>\(m\in\varnothing\)

b: Phương trình hoành độ giao điểm là:

\(x^2=mx-m+1\)

=>\(x^2-mx+m-1=0\)

\(\text{Δ}=\left(-m\right)^2-4\cdot1\left(m-1\right)\)

\(=m^2-4m+4=\left(m-2\right)^2\)

Để (d) cắt (P) tại hai điểm phân biệt thì Δ>0

=>(m-2)^2>0

=>\(m-2\ne0\)

=>\(m\ne2\)

Theo Vi-et, ta được:

\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=m\\x_1x_2=\dfrac{c}{a}=m-1\end{matrix}\right.\)

\(y_1+y_2=x_1+x_2\)

=>\(x_1^2+x_2^2=x_1+x_2\)

=>\(\left(x_1+x_2\right)^2-2x_1x_2-\left(x_1+x_2\right)=0\)

=>\(m^2-2\left(m-1\right)-m=0\)

=>\(m^2-3m+2=0\)

=>(m-2)(m-1)=0

=>\(\left[{}\begin{matrix}m=2\left(loại\right)\\m=1\left(nhận\right)\end{matrix}\right.\)

6) (2x - 1)/(x² - 4) + (x + 3)/(2 - x) + 5 = 0 (1)

ĐKXĐ: x ≠ 2; x ≠ -2

(1) ⇔ 2x - 1 - (x + 3)(x + 2) + 5(x² - 4) = 0

2x - 1 - x² - 5x - 6 + 5x² - 20 = 0

4x² - 3x - 27 = 0

4x² - 12x + 9x - 27 = 0

(4x² - 12x) + (9x - 27) = 0

4x(x - 3) + 9(x - 3) = 0

(x - 3)(4x + 9) = 0

⇒ x - 3 = 0 hoặc 4x + 9 = 0

*) x - 3 = 0

x = 3 (nhận)

*) 4x + 9 = 0

4x = -9

x = -9/4 (nhận)

Vậy S = {-9/4; 3}

5) x - 4/(x - 2) = 5 (1)

ĐKXĐ: x ≠ 2

(1) ⇔ x(x - 2) - 4 = 5(x - 2)

x² - 2x - 4 = 5x - 10

x² - 2x - 4 - 5x + 10 = 0

x² - 7x + 6 = 0

x² - x - 6x + 6 = 0

(x² - x) - (6x - 6) = 0

x(x - 1) - 6(x - 1) = 0

(x - 1)(x - 6) = 0

⇒ x - 1 = 0 hoặc x - 6 = 0

*) x - 1 = 0

x = 1 (nhận)

*) x - 6 = 0

x = 6 (nhận)

Vậy S = {1; 6}

4) 4x + 3/(x - 1) = 11 (1)

ĐKXĐ: x ≠ 1

(1) ⇔ 4x(x - 1) + 3 = 11(x - 1)

4x² - 4x + 3 = 11x - 11

4x² - 4x + 3 - 11x + 11 = 0

4x² - 15x + 14 = 0

4x² - 8x - 7x + 14 = 0

(4x² - 8x) - (7x - 14) = 0

4x(x - 2) - 7(x - 2) = 0

(x - 2)(4x - 7) = 0

⇒ x - 2 = 0 hoặc 4x - 7 = 0

*) x - 2 = 0

x = 2 (nhận)

*) 4x - 7 = 0

4x = 7

x = 7/4 (nhận)

Vậy S = {7/4; 2}

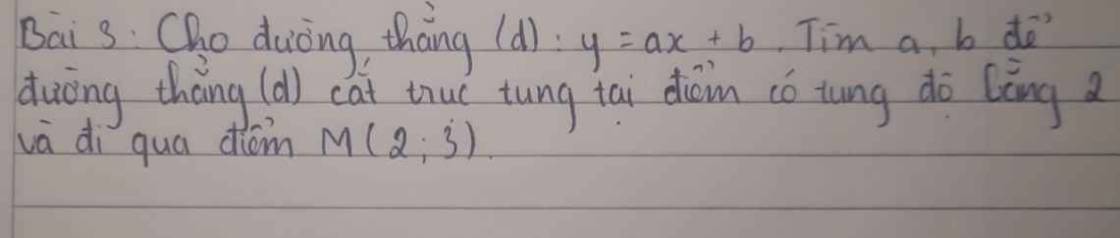
Lời giải:

Vì $(d)$ đi qua điểm $M(2,3)$ nên:

$y_M=ax_M+b\Leftrightarrow 3=2a+b(1)$

Vì $(d)$ cắt trục tung tại điểm có tung độ 2, tức là $(d)$ cắt trục tung tại điểm $(0,2)$

$\Rightarrow 2=a.0+b(2)$

Từ $(1); (2)\Rightarrow b=2; a=\frac{1}{2}$

cíu tui

2.16:

a: ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\\sqrt{x}-1< >0\end{matrix}\right.\)

=>x>=0 và x<>1

b: \(f\left(4-2\sqrt{3}\right)=\dfrac{\sqrt{4-2\sqrt{3}}+1}{\sqrt{4-2\sqrt{3}}-1}\)

\(=\dfrac{\sqrt{\left(\sqrt{3}-1\right)^2}+1}{\sqrt{\left(\sqrt{3}-1\right)^2}-1}=\dfrac{\sqrt{3}-1+1}{\sqrt{3}-1-1}\)

\(=\dfrac{\sqrt{3}}{-2+\sqrt{3}}=-\dfrac{\sqrt{3}}{2-\sqrt{3}}=-\sqrt{3}\left(2+\sqrt{3}\right)=-2\sqrt{3}-3\)

\(f\left(a^2\right)=\dfrac{\sqrt{a^2}+1}{\sqrt{a^2}-1}=\dfrac{-a+1}{-a-1}=\dfrac{a-1}{a+1}\)

c: \(f\left(x\right)=\sqrt{3}\)

=>\(\sqrt{x}+1=\sqrt{3}\cdot\sqrt{x}-\sqrt{3}\)

=>\(\sqrt{x}\left(1-\sqrt{3}\right)=-\sqrt{3}-1\)

=>\(\sqrt{x}\left(\sqrt{3}-1\right)=\sqrt{3}+1\)

=>\(\sqrt{x}=\dfrac{\sqrt{3}+1}{\sqrt{3}-1}\)

=>\(x=\dfrac{4+2\sqrt{3}}{4-2\sqrt{3}}=\dfrac{2+\sqrt{3}}{2-\sqrt{3}}=\left(2+\sqrt{3}\right)^2=7+4\sqrt{3}\)

d: f(x)=f(x^2)

=>\(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}=\dfrac{\left|x\right|+1}{\left|x\right|-1}\)

=>\(\left(\sqrt{x}+1\right)\left(\left|x\right|-1\right)=\left(\sqrt{x}-1\right)\left(\left|x\right|+1\right)\)

=>\(\sqrt{x}\cdot\left|x\right|-\sqrt{x}+\left|x\right|-1=\sqrt{x}\cdot\left|x\right|+\sqrt{x}-\left|x\right|-1\)

=>\(-2\sqrt{x}+2\left|x\right|=0\)

=>\(\left[{}\begin{matrix}x=0\left(nhận\right)\\x=1\left(loại\right)\end{matrix}\right.\)

Gọi (d): y = ax + b

Do đồ thị hàm số song song với đường thẳng y = 2x nên a = 2

⇒ (d): y = 2x + b

Do (d) cắt trục hoành tại điểm có hoành độ là -3 nên thay x = -3; y = 0 vào (d) ta được:

2.(-3) + b = 0

⇔ -6 + b = 0

⇔ b = 0 + 6

⇔ b = 6

Vậy (d): y = 2x + 6

Hàm số y = ax + b được yêu cầu là một đường thẳng song song với đường thẳng y = 2x và cắt trục hoành tại điểm có hoành độ -3. Để tìm hệ số a và b của hàm số, chúng ta có thể sử dụng hai điều kiện sau:

1. Đường thẳng y = ax + b song song với đường thẳng y = 2x, điều này có nghĩa là hệ số góc của đường thẳng y = ax + b phải bằng hệ số góc của đường thẳng y = 2x. Vậy a = 2.

2. Hàm số y = ax + b cắt trục hoành tại điểm có hoành độ -3, điều này có nghĩa là khi x = -3, y = 0 (vì nó cắt trục hoành). Chúng ta có thể sử dụng điều này để tìm giá trị của b.

Khi x = -3, ta có:

0 = 2(-3) + b
0 = -6 + b

Bây giờ hãy giải phương trình trên để tìm giá trị của b:

b = 6

Vậy hàm số y = 2x + 6 là hàm số song song với đường thẳng y = 2x và cắt trục hoành tại điểm có hoành độ -3.