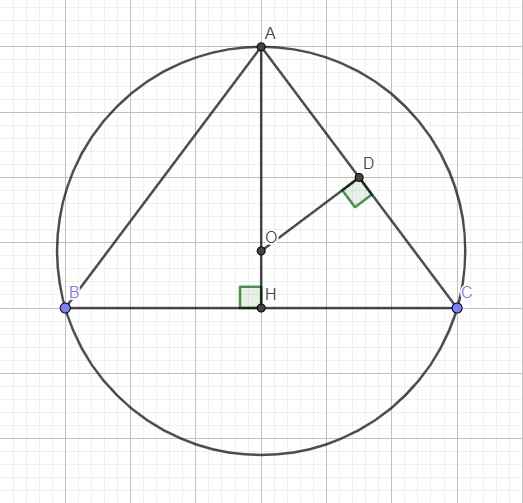
Tính đường cao của tam giác ABC cân tại A nội tiếp (O,25cm) biết AC=40cm
SR
Những câu hỏi liên quan
Cho tam giác ABC cân tại A nội tiếp đường tròn (O), AC = 40cm, BC = 48cm. Tính khoảng cách từ O đến BC.
Kẻ đường cao AH, ta tính được AH = 32cm.
Do AH > HC nên tâm O nằm giữa A và H. Đặt OH = x. Kẻ OM AC.
Ta có: (g.g)
.
Từ đó tính được x = 7cm.
Kẻ đường cao AH, ta tính được AH = 32cm.
Do AH > HC nên tâm O nằm giữa A và H. Đặt OH = x. Kẻ OM \bot AC.
Ta có: \Delta AMO \backsim \Delta AHC (g.g)
Xem thêm câu trả lời
Cho tam giác ABC cân tại A nội tiếp đường tròn (O), AC=40cm, BC=48cm. Tính
khoảng cách từ O đến BC.
Cho tam giác ABC cân tại A nội tiếp đường tròn (O), AC=40cm, BC=48cm. Tính
khoảng cách từ O đến BC.
Gọi H là trung điểm BC \(\Rightarrow AH\perp BC\) và O thuộc AH do tam giác ABC cân tại A
\(CH=\dfrac{1}{2}BC=24\left(cm\right)\)
Áp dụng Pitago: \(AH=\sqrt{AC^2-CH^2}=32\left(cm\right)\)
Gọi D là trung điểm AC \(\Rightarrow\) OD là trung trực AC hay \(OD\perp AC\)
\(AD=\dfrac{1}{2}AC=20\left(cm\right)\)
Hai tam giác vuông ADO và AHC đồng dạng (chung góc A)
\(\Rightarrow\dfrac{AD}{AH}=\dfrac{AO}{AC}\Rightarrow AO=\dfrac{AD.AC}{AH}=25\left(cm\right)\)
\(\Rightarrow OH=AH-AO=7\left(cm\right)\)
Đúng 1
Bình luận (0)
cho tam giác abc cân tại a nội tiếp đường tròn o, ac=40cm, bc=48cm.tính khoảng cách từ o đến bc
Cho tam giác ABC cân tại A, nội tiếp đường tròn (O). Đường cao AH cắt (O) ở D. Biết BC=24cm, AC=20cm. Tính chiều cao AH và bán kính đường tròn (O)
Cho tam giác ABC cân tại A nội tiếp đường tròn tâm O. Đường cao AH cắt đường tròn tại D
a) Vì sao AD lad đường kính của đường tròn tâm O
b) Cho biết AC = 10 cm, BC = 12 cm. Tính đường cao AH và BK của đường tròn tâm O
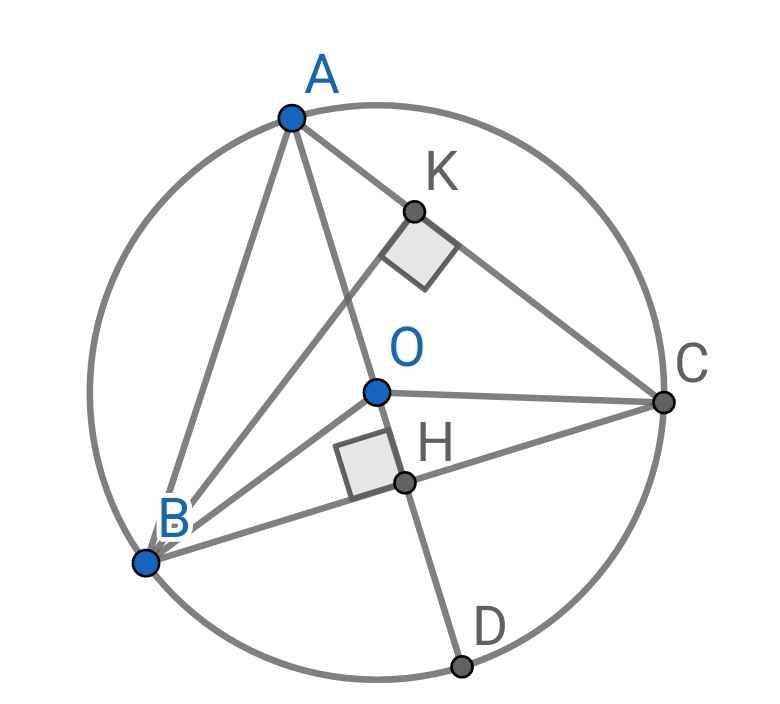 a) Ta có:
a) Ta có:
OB = OC (bán kính)
⇒ O nằm trên đường trung trực của BC (1)
Do ∆ABC cân tại A (gt)
AH là đường cao (gt)
⇒ AH cũng là đường trung trực của ∆ABC
⇒ AH là đường trung trực của BC (2)
Từ (1) và (2) suy ra O ∈ AH
⇒ O ∈ AD
Vậy AD là đường kính của (O)
b) Sửa đề: Tính độ dài các đường cao AH, BK của ∆ABC
Do AH là đường trung trực của BC (cmt)
⇒ H là trung điểm của BC
⇒ CH = BC : 2
= 12 : 2
= 6 (cm)
∆AHC vuông tại H
⇒ AC² = AH² + CH² (Pytago)
⇒ AH² = AC² - CH²
= 10² - 6²
= 64
⇒ AH = 8 (cm)
⇒ sinACH = AH/AC
= 4/5
⇒ ACH ≈ 53⁰
⇒ BCK ≈ 53⁰
∆BCK vuông tại K
⇒ sinBCK = BK/BC
⇒ BK = BC.sinBCK
= 10.sin53⁰
≈ 8 (cm)
Đúng 4
Bình luận (0)
Cho tam giác ABC cân tại A, nội tiếp đường tròn (O). Đường cao AH cắt đường tròn ở D. Cho BC = 24cm, AC = 20cm. Tính đường cao AH và bán kính đường tròn (O)
Ta có: AH ⊥ BC ⇒ HB = HC = BC/2 = 24/2 = 12(cm)
Áp dụng định lí Pitago vào tam giác vuông ACH ta có:
A C 2 = A H 2 + H C 2
Suy ra: A H 2 = A C 2 - H C 2 = 20 2 - 12 2 = 400 - 144 = 256
AH = 16 (cm)
Tam giác ACD vuông tại C nên theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
A C 2 = AH.AD ⇒ AD = A C 2 /AH = 20 2 /16 = 25 (cm)
Vậy bán kính của đường tròn (O) là: R = AD/2 = 25/2 = 12,5 (cm)
Đúng 0
Bình luận (0)
Cho tam giác ABC (AB AC) nội tiếp đường tròn (O; R) đường kính BC. Vẽ đường cao AH của tam giác ABC. Đường tròn tâm K đường kính AH cắt AB, AC lần lượt tại D và Ea, Chứng minh tứ giác ADHE là hình chữ nhật và AB.AD AE.ACb, Cho biết BC 25cm và AH 12cm. Hãy tính diện tích xung quanh và thể tích của hình tạo thành bởi khi cho tứ giác ADHE quay quanh AD
Đọc tiếp
Cho tam giác ABC (AB < AC) nội tiếp đường tròn (O; R) đường kính BC. Vẽ đường cao AH của tam giác ABC. Đường tròn tâm K đường kính AH cắt AB, AC lần lượt tại D và E
a, Chứng minh tứ giác ADHE là hình chữ nhật và AB.AD = AE.AC
b, Cho biết BC = 25cm và AH = 12cm. Hãy tính diện tích xung quanh và thể tích của hình tạo thành bởi khi cho tứ giác ADHE quay quanh AD
a, Ta có A E H ^ = A D H ^ = D A E ^ = 90 0 => Tứ giác ADHE là hình chữ nhật
Lại có AB.AD = AH2 = AE.AC nên AB.AD = AE.AC
b, HB = 9cm, HC = 16cm (Lưu ý: AB < AC nên HB < HC)
HD = 36 5 cm, HE = 48 5 cm, Sxq = 3456 25 πcm 2 , V = 62208 125 πcm 3
Đúng 0
Bình luận (0)
cho tam giác ABC cân tại A nội tiếp (O;10)biết đường cao AH bằng độ dài cạnh BC tính Sabc
giúp em với ạ
Cho tam giác ABC cân tại A, nội tiếp đường tròn (O). Đường cao AH cắt (O) tại D.
a) Giaỉ thích vì sao AD là đường kính của đường tròn (O)
b) Cho BC=24cm, AC=20cm. Tính AH và bán kính đường tròn (O)?