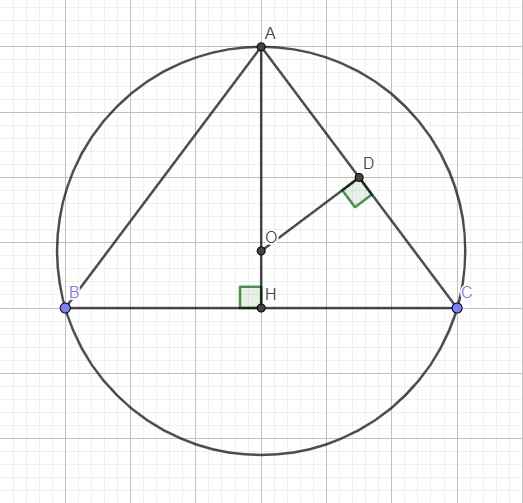
Gọi H là trung điểm BC \(\Rightarrow AH\perp BC\) và O thuộc AH do tam giác ABC cân tại A
\(CH=\dfrac{1}{2}BC=24\left(cm\right)\)
Áp dụng Pitago: \(AH=\sqrt{AC^2-CH^2}=32\left(cm\right)\)
Gọi D là trung điểm AC \(\Rightarrow\) OD là trung trực AC hay \(OD\perp AC\)
\(AD=\dfrac{1}{2}AC=20\left(cm\right)\)
Hai tam giác vuông ADO và AHC đồng dạng (chung góc A)
\(\Rightarrow\dfrac{AD}{AH}=\dfrac{AO}{AC}\Rightarrow AO=\dfrac{AD.AC}{AH}=25\left(cm\right)\)
\(\Rightarrow OH=AH-AO=7\left(cm\right)\)