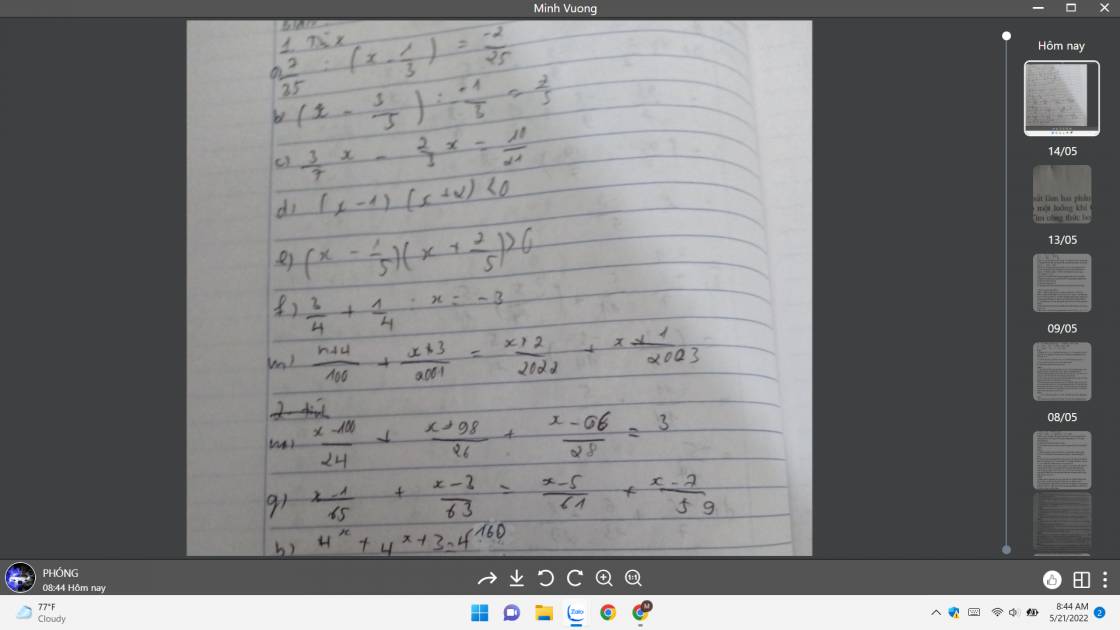
giải cho mình bài trong hình này với ạ
É ô ét ai giúp mình bài này với ạ, sẵn tiện giải thích cho mình với được ko ạ hiện giờ mình đang cần gấp lắm ạ mai mình thi rồi nên mong cao nhân nào giải bài với giải thích bài này cho mình với ạ
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}\) \(\dfrac{2^{11}.9^3}{3^5.16^2}\)
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.2^{32}}\)
Ta lấy vễ trên chia vế dưới
\(=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}\)
Ta lấy vế trên chia vế dưới
\(=2^3.3=24\)
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.3^{32}}=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}=2^3.3=8.3=24\)
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{3^{30}.2^{33}}{3^{29}.2^{32}}=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.3^6}{3^5.2^8}=2^3.3=8.3=24\)
Giúp mình 1 trong 2 bài này với ạ. Nếu được thì giải 2 bài này giúp mk với. Mình đang cần gấp lắm ạ 😢
jimmmmmmmmmmmmmmmmmmmmmmmmmmm
he he he he he he
bài 1:
bn lấy giá trị của √(4^2-3,9^2) là dc
bài 2
AB+BC=2√(3^2+4^2)=??
bài 10 : Hãy viết đề cho bài tập có lời giải là hình vẽ 4 ( trong VBT Toán 7 )
GIÚP mình giải bài này cái cần gấp bài này ai đã làm bảo mình với hình vẽ thì ở trong VBT toán 7 nhé tại vì mình ko biết vẽ hình trên mấy tính.
Giúp mình vẽ hình và giải bài được không ạ? Mai mình ktra e nhưng đọc bài vẫn ko vẽ được hình nên mình cần lấy bài này làm mẫu cho mấy bài tiếp theo. Mình cảm ơn ạ💜💜💜
a: Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
=>\(\widehat{AMB}=90^0\)
b: Xét ΔOMC vuông tại M có MH là đường cao
nên \(HC\cdot HO=HM^2\left(1\right)\)
Xét ΔMAB vuông tại M có MH là đường cao
nên \(HA\cdot HB=HM^2\left(2\right)\)
Từ (1) và (2) suy ra \(HC\cdot HO=HA\cdot HB\)
c: Xét tứ giác AMBQ có
O là trung điểm của AB và MQ
Do đó: AMBQ là hình bình hành
Hình bình hành AMBQ có AB=MQ
nên AMBQ là hình bình hành
 Các bạn giải cả 3 bài này giúp mình với, mình đang gấp nhớ vẽ hình lun ạ !!! Cảm ơn
Các bạn giải cả 3 bài này giúp mình với, mình đang gấp nhớ vẽ hình lun ạ !!! Cảm ơn
Giải cho mình bài này với ạ, mình đang cần gấp
Bài nào em nhỉ?
giải chi tiết cho mình bài này với ạ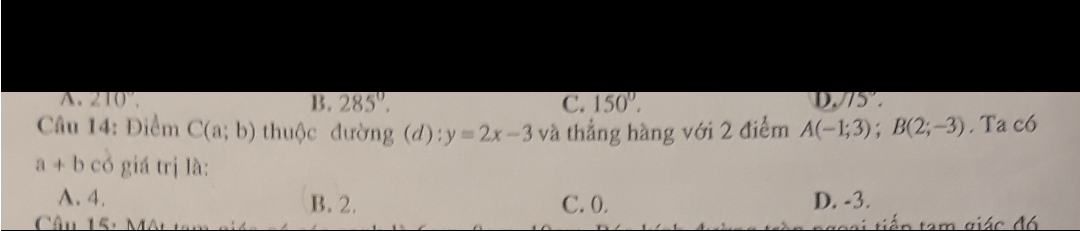
Gọi phương trình đường thẳng đi qua 2 điểm \(A,B\) là \(y=mx+n\)
Do \(\left\{{}\begin{matrix}A\in AB\\B\in AB\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}3=-m+n\\-3=2m+n\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m=-2\\n=1\end{matrix}\right.\)
\(\Rightarrow AB:y=-2x+1\)
Do \(C\left(a,b\right)\in\left(d\right):y=2x-3\Rightarrow b=2a-3\) (1)
Mặt khác, để \(A,B,C\) thẳng hàng thì \(C\in AB\Rightarrow b=-2a+1\) (2)
Từ (1) và (2) ta có \(a=1,b=-1\) nên \(a+b=0\)
Do C thuộc d nên: \(b=2a-3\) \(\Rightarrow C\left(a;2a-3\right)\)
Gọi phương trình đường thẳng d1 qua 2 điểm A; B có dạng:
\(y=mx+n\)
A; B thuộc d1 nên: \(\left\{{}\begin{matrix}3=-m+n\\-3=2m+n\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m=-2\\n=1\end{matrix}\right.\)
\(\Rightarrow\) Phương trình d1: \(y=-2x+1\)
A;B;C thẳng hàng khi và chỉ khi C thuộc d1
\(\Rightarrow2a-3=-2a+1\)
\(\Rightarrow4a=4\Rightarrow a=1\Rightarrow b=-1\)
\(\Rightarrow a+b=0\)
Mng ơi giải thích giúp mình bài này với ạ mình k hiểu cách giải cho lắm
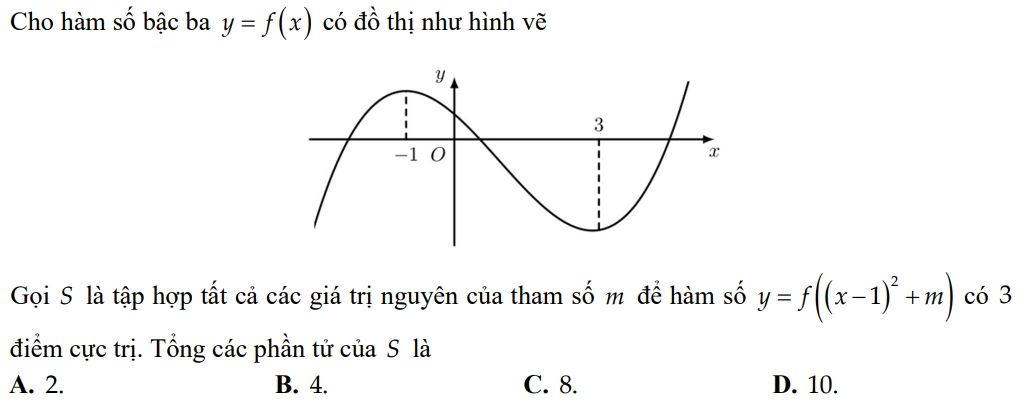
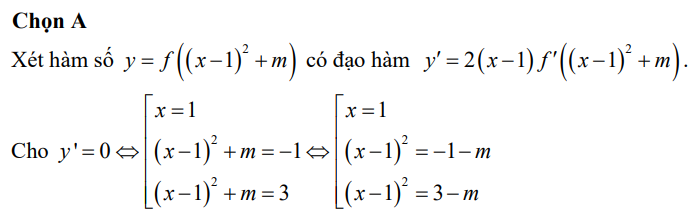
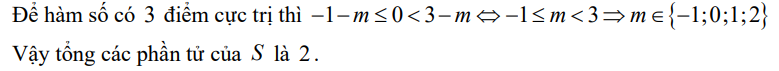
Bài này làm khá tắt chỗ 3 điểm cực trị, mình trình bày lại để bạn dễ hiểu nhé!
.......
Để y' = 0\(\Leftrightarrow\left[{}\begin{matrix}x=1\\f'\left(\left(x-1\right)^2+m\right)=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=1\\\left(x-1\right)^2+m=-1\\\left(x-1\right)^2+m=3\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=1\\\left(x-1\right)^2=-1-m\left(1\right)\\\left(x-1\right)^2=3-m\left(2\right)\end{matrix}\right.\)
Để hàm số có 3 điểm cực trị thì y' = 0 có 3 nghiệm phân biệt.
Ta có 2 trường hợp.
+) \(TH_1:\) (1) có nghiệm kép x = 1 hoặc vô nghiệm và (2) có hai nghiệm phân biệt khác 1.
\(\Rightarrow\left[{}\begin{matrix}-1-m\le0\\3-m>0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}m\ge-1\\m< 3\end{matrix}\right.\) \(\Leftrightarrow-1\le m< 3\)
+) \(TH_2:\) (2) có nghiệm kép x = 1 và (2) có một nghiệm phân biệt khác 1.
\(\Rightarrow\left[{}\begin{matrix}-1-m>0\\3-m\le0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}m< -1\\m\ge3\end{matrix}\right.\) \(\Leftrightarrow m\in\varnothing\)
\(\Rightarrow-1\le m< 3\Rightarrow S=\left\{-1;0;1;2\right\}\)
Do đó tổng các phần tử của S là \(-1+0+1+2=2\)
giải gấp cho mình bài này với ạ, cảm ơn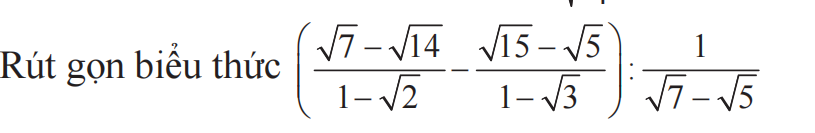
\(=\left[\dfrac{\sqrt{7}\left(1-\sqrt{2}\right)}{1-\sqrt{2}}+\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}\right]\cdot\left(\sqrt{7}-\sqrt{5}\right)\\ =\left(\sqrt{7}+\sqrt{5}\right)\left(\sqrt{7}-\sqrt{5}\right)=7-5=2\)