tại sao Trong một tam giác, tổng độ dài hai cạnh bất kì luôn lớn hơn cạnh còn lại , là sai
TV
Những câu hỏi liên quan
3 đường cao của 1 tam giác có độ dài là 4;12;x biết rằng x thuộc N.Biết rằng tổng 2 cạnh của tam giác luôn lớn hơn cạnh còn lại và 1canhj bất kì luôn lớn hơn hiệu của 2 cạnh còn lại.Tìm x
Có hay không một tam giác có độ dài ba cạnh tỉ lệ với các số 3;4;9?
Chú ý: Trong một tam giác tổng độ dài hai cạnh bao giờ cũng lớn hơn độ dài cạnh còn lại
Gọi độ dài 3 cạnh của tam giác thứ tự là a,b,c (a > 0; b > 0; c > 0).
Vì độ dài 3 cạnh tỉ lệ với 3, 4, 9 nên:
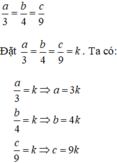
Suy ra: a + b = 3k + 4k = 7k < 9k (hay a + b < c)
Điều này mâu thuẫn (một cạnh tam giác bao giờ cũng nhỏ hơn tổng hai cạnh còn lại)
Vậy không có tam giác nào có 3 cạnh tỉ lệ 3;4;9.
Đúng 0
Bình luận (0)
Một tứ giác lồi có độ dài bốn cạnh đều là số tự nhiên sao cho tổng ba số bất kì trong chúng chia hết cho số còn lại. Chứng minh rằng tứ giác đó có ít nhất hai cạnh bằng nhau.
Nhập 3 số a,b,c.Kiểm trả xem nó thoả mãn độ dài của một tam giác không.Biết tổng chiều dài 2 cạnh luôn lớn hơn cạnh còn lại và ba cạnh có chiều dài lớn hơn 0 thì thoả mãn
#include <iostream>
using namespace std;
int main()
{
int a,b,c,kt;
cout<<"Nhap a=";
cin>>a;
cout<<"Nhap b=";
cin>>b;
cout<<"Nhap c=";
cin>>c;
if ((a>0) and (b>0) and (c>0) and (a+b>c) and (a+c>b) and (b+c>a)) cout<<"Day la ba canh trong mot tam giac";
else cout<<"Day khong la ba canh trong mot tam giac";
return 0;
}
Đúng 0
Bình luận (0)
Một tứ giác lồi có độ dài bốn cạnh đều là số tự nhiên sao cho tổng ba số bất kì trong chúng chia hết cho số còn lại. Chứng minh rằng tứ giác đó có ít nhất hai cạnh bằng nhau.
Có hay không một tam giác có độ dài ba cạnh tỉ lệ với các số 3 : 4 : 9 ?
Chú ý : Trong một tam giác, tổng độ dài hai cạnh bao giờ cũng lớn hơn độ dài cạnh còn lại ?
Gọi độ dài 3 cạnh của tam giác thứ tự là a, b, c.
Theo đề bài ta có: a3=b4=c9a3=b4=c9
Đặt các tỉ số trên là k. Ta có:
a3=k⇒a=3ka3=k⇒a=3k
b4=k⇒b=4kb4=k⇒b=4k
c9=k⇒c=9kc9=k⇒c=9k
Suy ra: a + b = 3k + 4k = 7k < 9k
Điều này mâu thuẫn (một cạnh tam giác bao giờ cũng nhỏ hơn tổng hai cạnh còn lại).
Vậy không có tam giác nào có 3 cạnh tỉ lệ với 3; 4; 9.
Đúng 0
Bình luận (0)
CMR:Trong 1 tứ giác
a,độ dài bất kì của cạnh nào cũng bé hơn tổng độ dài 3 cạnh còn lại
b,tổng độ dài 2 đường chéo lớn hơn nửa chu vi và bé hơn nửa chu vi tứ giác đó
cho tam giác abc ;các đường phân giác của góc A và góc B cắt tại O.qua O kẻ đường thẳng song song với AB ,cắt BC tại M và cắt AC tại N.Tìm các hình thang trên hình vẽ(có giải thích)
Biết độ dài ba cạnh của một tam giác tỉ lệ thuận với 3 ;5;7 . Biết tổng độ dài của cạnh lớn nhất và cạnh nhỏ nhất lớn hơn cạnh còn lại là 20m . Tính cạnh nhỏ nhất của tam giác
A. 20m
B. 12m
C. 15m
D. 16m
Gọi x,y,z là ba cạnh của tam giác (x,y,z > 0)
Gỉa sử x,y,z tỉ lệ thuận với 3 ;5;7 ta có: x 3 = y 5 = z 7
Thì x là cạnh nhỏ nhất và z là cạnh lớn nhất của tam giác . Khi đó theo bài ta có x + z - y = 20
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
x 3 = y 5 = z 7 = x + y − z 3 − 5 + 7 = 20 5 = 4
Do đó x = 4.3 = 12
Vậy cạnh nhỏ nhất của tam giác là 12m
Đáp án cần chọn là B
Đúng 0
Bình luận (0)
Tam giác ABC có độ dài ba cạnh tỉ lệ với 3, 4, 5 và độ dài cạnh lớn nhất nhỏ hơn tổng độ dài hai cạnh còn lại là 10 cm. Hãy tính độ dài ba cạnh của tam giác ABC.
Giải:
Gọi 3 cạnh của tam giác ABC lần lượt là a, b, c ( a > b > c > 0 )
Ta có: \(\frac{a}{5}=\frac{b}{4}=\frac{c}{3}\) và a - c = 10
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{5}=\frac{b}{4}=\frac{c}{3}=\frac{a-c}{5-3}=\frac{10}{2}=5\)
+) \(\frac{a}{5}=5\Rightarrow a=25\)
+) \(\frac{b}{4}=5\Rightarrow b=20\)
+) \(\frac{c}{3}=5\Rightarrow c=15\)
Vậy 3 cạnh của tam giác lần lượt là 15 cm, 20 cm và 25 cm
Đúng 0
Bình luận (0)
Gọi độ dài các cạnh của tam giác lần lượt là a , b , c (theo thứ tự nhỏ đến lớn)
Theo đề bài , ta có :
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\) và c + 10 = a + b
Áp dụng tính chất dãy tỉ số bằng nhau , ta có:
\(\frac{a}{3}=\frac{b}{4}=\frac{a+b}{3+4}=\frac{c+10}{7}\)
=> \(\frac{c+10}{7}=\frac{c}{5}\)
=> 5(c + 10) = 7c
=> 5c + 50 = 7c
=> 50 = 2c
=> c = 25
=> a + b = 25 + 10 = 35
Áp dụng tính chất dãy tỉ số , ta có :
\(\frac{a}{3}=\frac{b}{4}=\frac{a+b}{3+4}=\frac{35}{7}=5\)
=> a = 3.5 = 15
b = 4.5 = 20
Đúng 0
Bình luận (0)
Gọi các cạnh lần lượt là a ; b ; c ta có a/3 = b/4=c/5
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
a/3 = b/4 = c/5 = \(\frac{b+c-a}{4+5-3}\) = 10/6 cm =5/3 cm
từ đó suy ra :
a/3 = 5/3 cm\(\Rightarrow\) a = 5 cm
b/4 = 5/3 cm \(\Rightarrow\) b = 5/3cm*4=20/3cm
c/5 = 5/3 cm\(\Rightarrow\) c = 5/3 cm *5 =25/3 cm
Vậy a = 5 cm;b = 20/3 cm ; c = 25/3 cm
Đúng 0
Bình luận (0)