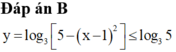Tìm GTLN của A=3-x2+2x-(y-3)
UN
Những câu hỏi liên quan
tìm GTNN hoặc GTLN của A = 3x2+2x-3
B = (x2+x+20): x2 +x +5
A=3(x^2+2/3x-1)
=3(x^2+2*x*1/3+1/9-10/9)
=3(x+1/3)^2-10/3>=-10/3
Dấu = xảy ra khi x=-1/3
\(B=1+\dfrac{15}{x^2+x+5}=1+\dfrac{15}{\left(x+\dfrac{1}{2}\right)^2+\dfrac{19}{4}}< =1+15:\dfrac{19}{4}=1+\dfrac{60}{19}=\dfrac{79}{19}\)
Dấu = xảy ra khi x=-1/2
Đúng 2
Bình luận (1)
Biết x2+4y2+9z2=3 Tìm GTLN của S=2x+4y+6x
Cho x;y ∈ 𝑅 thỏa mãn x2+y2 -xy=4 . Tìm giá trị lớn nhất và nhỏ nhất của C= x2+y2
a) Áp dụng bất đẳng thức Cosi ta có :
\(x^2+1\geq 2x\\ 4y^2+1\geq 4y\\ 9z^2+1\geq 6z\)
Suy ra \(S\leq 6\)
Dấu = xảy ra khi \(x=1;y=\frac{1}{2}; z=\frac{1}{3}\)
Đúng 0
Bình luận (0)
Tìm GTLN hoặc GTNN của các đa thưc sau:
Xem chi tiết
a, -x2 + 2x + 3
b, x2 - 2x + 4y2 - 4y + 8 c, -x2 - y2 + xy + 2x + 2y + 4 d, x2 + 5y2 - 4xy - 2y + 2015 e, 2x2 + y2 + 6x + 2y + 2xy + 2018A= -x2+2x+3
=>A= -(x2-2x+3)
=>A= -(x2-2.x.1+1+3-1)
=>A=-[(x-1)2+2]
=>A= -(x+1)2-2
Vì -(x+1)2 ≤0=> A≤-2
Dấu "=" xảy ra khi
-(x+1)2=0 => x=-1
Vây A lớn nhất= -2 khi x= -1
Đúng 4
Bình luận (0)
B=x2-2x+4y2-4y+8
=> B= (x2-2x+1)+(4y2-4y+1)+6
=> B=(x-1)2+(2y+1)2+6
=> B lớn nhất=6 khi x=1 và y=-1/2
Đúng 2
Bình luận (0)
1. Cho x,y thỏa mãn: x2 + 5y2 - 4xy + 2y = 3. Tìm x,y sao cho x đạt GTLN
2. Cho x,y thỏa mãn: 3x2 + y2 + 2xy + 4 = 7x + 3y
a) Tìm GTNN, GTLN của biểu thức P = x + y
b) Tìm GTNN, GTLN của x
3. Cho x,y thỏa mãn: x2 + 2y2 + 2xy + 7x + 7y + 10 = 0. Tìm GTLN, GTNN của S = x + y
tìm m để PT: x2-2x-(m-1)(m-3)=0
cps 2 nghiệm x1,x2: A= (x1+1)x2 đạt GTLN
tìm m để PT x2-2x-(m-1)(m-3)=0 có 1 nghiệm x1,x2: A= (x1+1)x2 đạt GTLN
tìm m để PT x2-2x-(m-1)(m-3)=0 có 1 nghiệm x1,x2: A= (x1+1)x2 đạt GTLN
Tìm GTLN của BT
-x2+2xy-4y2+2x+10y-8
-x2-y2+xy+x+y
Tìm GTLN (max) của hàm số
y
log
3
4
+
2
x
-
x
2
A.
log
3
4
B.
log
3
5
C.
5
3
D. ...
Đọc tiếp
Tìm GTLN (max) của hàm số y = log 3 4 + 2 x - x 2
A. log 3 4
B. log 3 5
C. 5 3
D. 1 + 3
tìm m để pt: x2 - 2x - (m - 1)(m - 3) = 0 có 2 nghiệm x1, x2 sao cho A = (x1 + 1).x2 đạt GTLN
Lời giải:
Để pt có 2 nghiệm $x_1,x_2$ thì:
$\Delta'=1+(m-1)(m-3)\geq 0\Leftrightarrow (m-2)^2\geq 0\Leftrightarrow m\in\mathbb{R}$
Ta có:
$x^2-2x-(m-1)(m-3)=0$
$\Leftrightarrow [x-(m-1)][x+(m-3)]=0$
$\Rightarrow (x_1,x_2)=(m-1,3-m)$ và hoán vị
Nếu $x_1=m-1; x_2=3-m$ thì: $A=(x_1+1)x_2=m(3-m)=3m-m^2=\frac{9}{4}-(m-\frac{3}{2})^2\leq \frac{9}{4}$
Vậy $A_{\max}=\frac{9}{4}$ khi $m=\frac{3}{2}$
Nếu $x_1=3-m; x_2=m-1$ thì:
$A=(4-m)(m-1)=5m-4-m^2=\frac{9}{4}-(m-\frac{5}{2})^2\leq \frac{9}{4}$
Vậy $A_{\max}=\frac{9}{4}$ khi $m=\frac{5}{2}$
Vậy tóm lại $m=\frac{3}{2}$ hoặc $m=\frac{5}{2}$ thì $A_{\max}$
Đúng 1
Bình luận (0)