Cho tam giác ABC vuông tại A có AB = 9 cm ; BC = 15 cm
a, Tính AC và so sánh các góc của tam giác ABC
b, Lấy D thuộc tia đối của AB sao cho A là trung điểm của BD. Chứng minh tam giác BCD cân
c, Lấy E là trung điểm BC và BK cắt AC tại M. Tính MC
1. Cho tam giác ABC vuông tại A có AB = 9 cm , BC = 15 cm , AH là đường C10 ( H thuộc cạnh BC ) . Tính BH , CH , AC và AH ,
2. Cho tam giác ABC vuông tại A có AC = 5 cm , AB = 4 cm . Tính : a ) Cạnh huyền BC . b ) Hình chiếu của AB và AC trên cạnh huyền . c ) Đường cao AH .
3. Cho tam giác ABC vuông tại A có BC = 40 cm , AC = 36 cm . Tính AB , BH , CH và AH ,
4. Cho tam giác ABC vuông tại A có BC = 24 cm . Tính AB , AC , cho biết 2 AB = -AC .
5. Cho tam giác ABC vuông tại A có AH là đường cao . BH = 10 cm , CH = 42 cm . Tính BC , AH , AB và AC ,
6. Cho đường tròn tâm O bán kính R = 10 cm . A , B là hai điểm trên đường tròn ( O ) và I là trung điểm của đoạn thẳng AB . a ) Tính AB nếu OI = 7 cm . b ) Tính OI nếu AB = 14 cm .
Bài 1:
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=15^2-9^2=144\)
hay AC=12(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{9^2}{15}=\dfrac{81}{15}=5.4\left(cm\right)\\CH=\dfrac{12^2}{15}=\dfrac{144}{15}=9,6\left(cm\right)\end{matrix}\right.\)
Áp dụng định lí Pytago vào ΔAHB vuông tại H, ta được:
\(AH^2+HB^2=AB^2\)
\(\Leftrightarrow AH^2=9^2-5.4^2=51,84\)
hay AH=7,2(cm)
1. Cho tam giác ABC vuông tại A có AB = 9 cm , BC = 15 cm , AH là đường C10 ( H thuộc cạnh BC ) . Tính BH , CH , AC và AH ,
2. Cho tam giác ABC vuông tại A có AC = 5 cm , AB = 4 cm . Tính : a ) Cạnh huyền BC . b ) Hình chiếu của AB và AC trên cạnh huyền . c ) Đường cao AH .
3. Cho tam giác ABC vuông tại A có BC = 40 cm , AC = 36 cm . Tính AB , BH , CH và AH ,
4. Cho tam giác ABC vuông tại A có BC = 24 cm . Tính AB , AC , cho biết 2 AB = -AC .
5. Cho tam giác ABC vuông tại A có AH là đường cao . BH = 10 cm , CH = 42 cm . Tính BC , AH , AB và AC ,
6. Cho đường tròn tâm O bán kính R = 10 cm . A , B là hai điểm trên đường tròn ( O ) và I là trung điểm của đoạn thẳng AB . a ) Tính AB nếu OI = 7 cm . b ) Tính OI nếu AB = 14 cm .
Cho tam giác ABC vuông tại A ,có phân giác BD, biết AB = 9 cm, BC = 15 cm .Tính AC, DC, DA?
Theo định lí Pytago tam giác ABC vuông tại A
\(AC=\sqrt{BC^2-AB^2}=12cm\)
Vì BD là pg \(\dfrac{AB}{BC}=\dfrac{AD}{DC}\Rightarrow\dfrac{DC}{BC}=\dfrac{AD}{AB}\)
Theo tc dãy tỉ số bằng nhau ta có
\(\dfrac{DC}{BC}=\dfrac{AD}{AB}=\dfrac{12}{24}=\dfrac{1}{2}\Rightarrow DC=\dfrac{15}{2}cm;DA=\dfrac{9}{2}cm\)
Cho tam giác ABC vuông tại A có AB = 9 cm, AC = 12 cm. Gọi I là tâm đường tròn nội tiếp tam giác ABC, G là trọng tâm của tam giác ABC. Tính độ dài IG
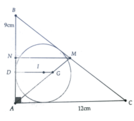
Gọi M là trung điểm của BC
Ta tính được AG = 2 3 AM = 10cm
Gọi N là trung điểm của AB => MN//AC, MN ⊥ AB
D,I,G thẳng hàng
<=> A G A M = A D A N = 2 3 <=> A D 2 A N = 1 3 <=> A D A B = 1 3
Ta có AD = r nội tiếp = A B + A C - B C 2 <=> A B 3 = A B + A C - B C 2
<=> AB+3AC = 3BC = A B 2 + A C 2
<=> 3AC = 4AB (đpcm)
Áp dụng kết quả trên ta có: AD = A B + A C - B C 2 = 3cm
=> ID = DA = 3cm => IG = DG – ID = 1cm
1/ Cho tam giác ABC vuông tại A có đường phân giác AD và đường trung tuyến BM vuông góc tại E. Gọi H là trung điểm AE. BE cắt AC tại K.
a) Cm: tam giác BDK vuông cân tại D
b) Cm : (AD/AC)2 = 2/9
2/ Cho tam giác ABC vuông cân tại có đường trung tuyến AM. Vẽ MH vuông AB ( H thuộc AB ). Từ A hạ AI vuông CH tại I. Gọi N là giao điểm IC và AM. BI cắt AC tại K.
a) Cm: BI vuông với IM tại I
b) Cm: AN.AB = IC.MK
cho tam giác ABC vuông tại A có AC =20 cm kẻ AH vuông goc BC. biết BH=9 cm, HC=16cm. Tính AB,AH
vì BH=9 , HC=16
=> BC=25
xét tam giác ABC ...., ta có
BC^2=CA^2+AB^2
hay 25^2=20^2 +Ab^2
625=400 + AB^2
AB^2=225
AB=15
xét tam giác ABH...., ta có
AB^2=AH^2 + BH^2
hay 15^2= Ah^2 + 9^2
225= AH^2 +81
AH^2= 144
AH=12
thêm kl và những chỗ còn thiếu vào nhé
cho tam giác ABC vuông tại A có AC =20 cm kẻ AH vuông goc BC. biết BH=9 cm, HC=16cm. Tính AB,AH

Ta có: \(BC=BH+CH=9+16=25\)
Áp dụng định lý Py- ta - go vào \(\Delta ABC\), ta được:
\(AB^2=BC^2-AC^2\)
\(\Leftrightarrow AB^2=25^2-20^2\)
\(\Leftrightarrow AB^2=625-400\)
\(\Leftrightarrow AB^2=225\)
\(\Leftrightarrow AB=\sqrt{225}=15\)
Áp dụng định lý Py- ta - go vào \(\Delta AHC\), ta được:
\(AH^2=AC^2-CH^2\)
\(\Leftrightarrow AH^2=20^2-16^2\)
\(\Leftrightarrow AH^2=400-256\)
\(\Leftrightarrow AH^2=144\)
\(\Leftrightarrow AH=\sqrt{144}=12\)
Bài làm
BC=BH+HC=9+6=25(cm)BC=BH+HC=9+6=25(cm)
Áp dụng định lý Py-ta-go với tam giác ABC vuông tại A, ta có:
BC2=AB2+AC2BC2=AB2+AC2
⇒AB2=BC2+AC2=252−202⇒AB2=BC2+AC2=252−202
=625−400=225=152=625−400=225=152
Vậy AB=15cm
Áp dụng định lý Py-ta-go với tam giác AHC vuông tại H, ta có:
AH2=AC2−HC2=202−162=122AH2=AC2−HC2=202−162=122
Vậy AH= 12cm
# Học tốt #
Bài làm
~ Vừa rồi mik viết thiếu mũ nhá. ~
Ta có : BC = BH + HC = 9 + 16 = 25 (cm)
Tam giác ABC vuông tại A nên :
BC2 = AB2 + AC2
252 = AB2 + 162
=> AB2 = 252 - 202
AB2 = 625 - 400 = 225 = 152
=> AB = 15 (cm)
Tam giác AHC vuông tại H nên :
AC2 = AH2 + HC2
202 = AH2 + 162
=> AH2 = 202 - 162
AH = 400 - 256 = 144 = 122
=> AH = 12 (cm)
Vậy AB = 15 cm ; AH = 12 cm
# Học tốt #
Cho tam giác ABC vuông tại A ,AB bằng 9 cm ,AC bằng 12 cm .Kẻ AH vuông góc với BC tại H
a/Chứng minh tam giác abh đồng dạng tam giác ABC và AB mũ 2 = Hb . BC
b/tính BC, ah
c/tia phân giác góc ACB cắt ah tại I và cắt AB tại D Chứng minh CB.CI=CA.CDCD
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
=>BH/BA=BA/BC
=>BA^2=BH*BC
b: BC=căn 9^2+12^2=15cm
AH=9*12/15=7,2cm
Cho Tam giác ABC vuông tại a có ab 8 cm, ac = 7, bc= 10 cm chứng minh Tam giác abc vuông ?
Cho Tam giác ABC vuông tại a có ab 8 cm, ac = 7, bc= 10 cm chứng minh Tam giác abc vuông