Giúp mik b3 vs ạ
MN
Những câu hỏi liên quan
cho a+b+c=0, tính M= a3 +b3+a2c+b2c-abc
giải giúp mik câu này vs ạ, mik cảm ơn nhìu
\(a^3+b^3+a^2c+b^2c-abc=a^2\left(a+b+c\right)+bc\left(b-a\right)=bc\left(b-a\right)\)
Đúng 0
Bình luận (0)
Làm cho mik b3 vs ah giúp mik vs mai mik nộp r 
a: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
Do đó: ADHE là hình chữ nhật
Đúng 0
Bình luận (0)
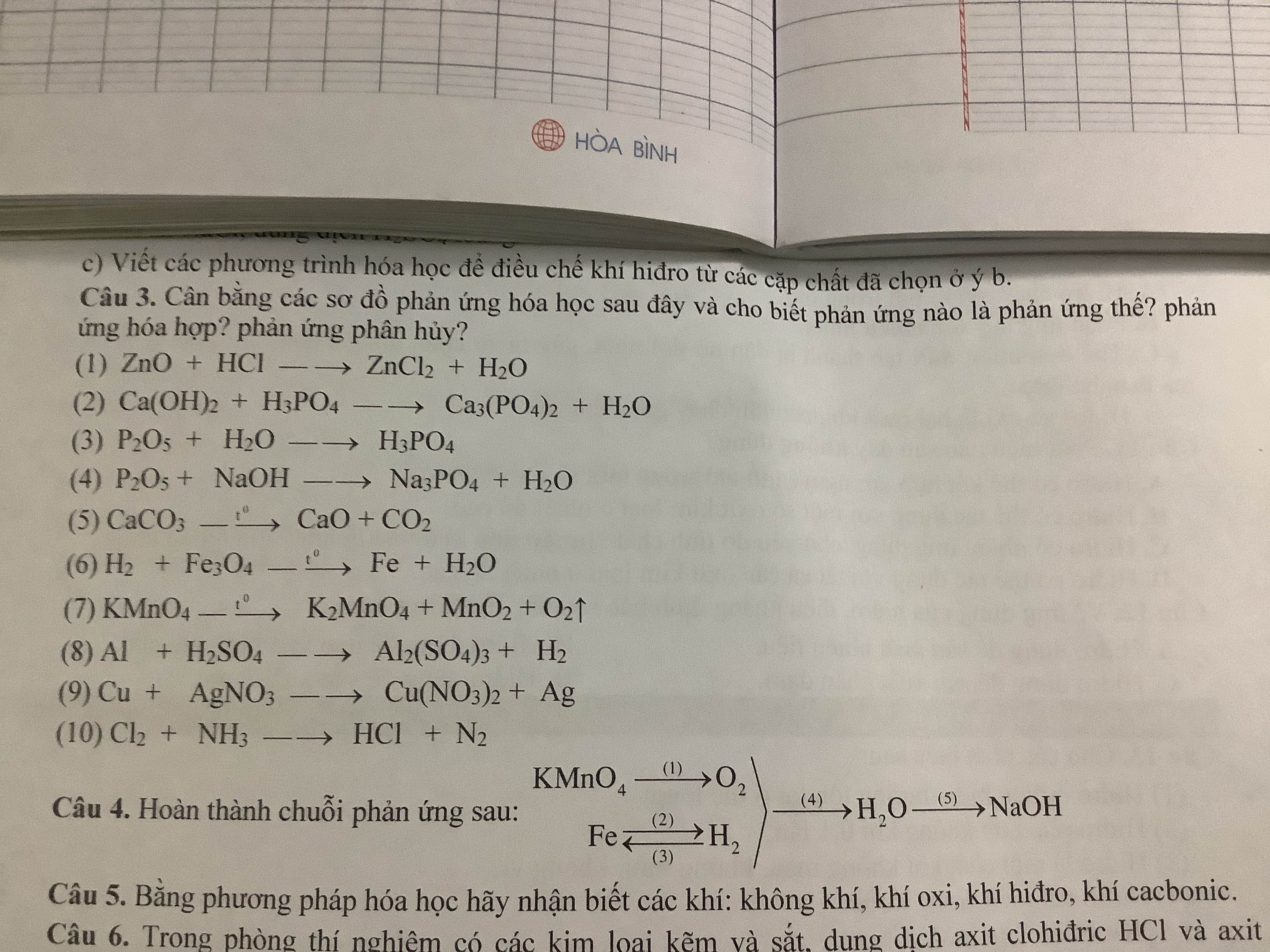 Giúp mi b3 vs ạ
Giúp mi b3 vs ạ
Câu 3:
\(\left(1\right)ZnO+2HCl\rightarrow ZnCl_2+H_2O\\ \left(2\right)3Ca\left(OH\right)_2+2H_3PO_4\rightarrow Ca_3\left(PO_4\right)_2+6H_2O\\ \left(3\right)P_2O_5+3H_2O\rightarrow2H_3PO_4\\ \left(4\right)P_2O_5+6NaOH\rightarrow2Na_3PO_4+H_2O\\ \left(5\right)CaCO_3\underrightarrow{t^o}CaO+CO_2\\ \left(6\right)4H_2+Fe_3O_4\underrightarrow{t^o}3Fe+4H_2O\)
\(\left(7\right)2KMnO_4\underrightarrow{t^o}K_2MnO_4+MnO_2+O_2\\ \left(8\right)2Al+3H_2SO_4\rightarrow Al_2\left(SO_4\right)_3+3H_2\\ \left(9\right)Cu+2AgNO_3\rightarrow Cu\left(NO_3\right)_2+2Ag\downarrow\)
Câu 4:
\(\left(1\right)2KMnO_4\underrightarrow{t^o}K_2MnO_4+MnO_2+O_2\\ \left(2\right)Fe+2HCl\rightarrow FeCl_2+H_2\\ \left(3\right)FeO+H_2\underrightarrow{t^o}Fe+H_2O\\ \left(4\right)2H_2+O_2\underrightarrow{t^o}2H_2O\\ \left(5\right)Na_2O+H_2O\rightarrow2NaOH\)
Câu 5:
Cho thử que đóm còn đang cháy:
- Cháy mãnh liệt -> O2
- Cháy màu xanh nhạt -> H2
- Cháy yếu -> kk
- Vụt tắt -> CO2
Đúng 0
Bình luận (0)
Giúp mik b3 vs ah mai nộp r 
Bài 3:
a: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
Do đó: ADHE là hình chữ nhật
Đúng 0
Bình luận (0)
lm hết cho mik vs câu a,b,c kẻ hình nữa
Đúng 0
Bình luận (0)
Giúp minh b2 vs b3 với ạ:< Cần gấp:')
2.
a.
\(P=\dfrac{1}{x+5}+\dfrac{2}{x-5}-\dfrac{2\left(x+5\right)}{\left(x-5\right)\left(x+5\right)}\)
\(=\dfrac{1}{x+5}+\dfrac{2}{x-5}-\dfrac{2}{x-5}=\dfrac{1}{x+5}\)
b.
\(P=-3\Rightarrow\dfrac{1}{x+5}=-3\Rightarrow x+5=-\dfrac{1}{3}\)
\(\Rightarrow x=-\dfrac{16}{3}\)
Thay vào bấm máy ta được \(Q=529\)
3.
a. \(P=\dfrac{3\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}+\dfrac{x+3}{\left(x-3\right)\left(x+3\right)}+\dfrac{18}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{3\left(x-3\right)+x+3+18}{\left(x-3\right)\left(x+3\right)}=\dfrac{4x+12}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{4\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{4}{x-3}\)
b.
\(P=4\Rightarrow\dfrac{4}{x-3}=4\Rightarrow x-3=1\)
\(\Rightarrow x=4\)
Đúng 0
Bình luận (0)
Cho A1=B1 Chứng minh a)A1=B3, A4=B2 b)A2=B2, A3=B3, A4=B4 c)A2+B1=180°,A4+B3=180°
giúp mik vs
a, \(\widehat{B}_1=\widehat{B_3}\) đối đỉnh
\(\widehat{A}_1=\widehat{B}_1\) theo bài đầu
Do đó \(\widehat{A_1}=\widehat{B_3}\)
Mặt khác,ta có \(\widehat{A_1}+\widehat{A_4}=180^0\) hai góc kề bù
=> \(\widehat{A_4}=180^0-\widehat{A_1}\) \((1)\)
Và \(\widehat{B_2}+\widehat{B_3}=180^0\) hai góc kề bù
=> \(\widehat{B_2}=180^0-\widehat{B_3}\) \((2)\)
\(\widehat{A_1}=\widehat{B_3}\) \((3)\)
Từ 1,2,3 ta có : \(\widehat{A_4}=\widehat{B_2}\)
b, \(\widehat{A_2}=\widehat{A_4}\) đối đỉnh
\(\widehat{A_4}=\widehat{B_2}\) theo câu a
Do đó : \(\widehat{A_2}=\widehat{B_2};\widehat{A_1}=\widehat{A_3}\) đối đỉnh
\(\widehat{A_1}=\widehat{B_3}\) câu a
Do đó \(\widehat{A_3}=\widehat{B_3}\). Mặt khác \(\widehat{B_2}=\widehat{B_4}\) hai góc đối đỉnh
\(\widehat{A_4}=\widehat{B_2}\) câu a . Do đó \(\widehat{A_4}=\widehat{B_4}\)
c, \(\widehat{B_1}+\widehat{B_2}=180^0\) hai góc kề bù
\(\widehat{A_1}=\widehat{B_1}\) theo đầu bài
Do đó \(\widehat{A_1}+\widehat{B_2}=180^0\)
Mặt khác \(\widehat{B_2}+\widehat{B_3}=180^0\) kề bù
\(\widehat{A_4}=\widehat{B_2}\) theo câu a . Do đó \(\widehat{A_4}+\widehat{B_3}=180^0\)
Đúng 0
Bình luận (0)
 giúp mik với ạ mik cần gấp. GIẢI CỤ THỂ GIÚP MIK vs ạ
giúp mik với ạ mik cần gấp. GIẢI CỤ THỂ GIÚP MIK vs ạ
`@` `\text {Ans}`
`\downarrow`
`4,`
Vì `\text {MN // BC}`
`=>` $\widehat {B} = \widehat {BMN} = 114^0 (\text {2 góc đối đỉnh})$
Ta có: \(\left\{{}\begin{matrix}\widehat{\text{BMN}}+\widehat{\text{AMN}}=180^0\left(\text{2 góc kề bù}\right)\\\widehat{\text{CNM}}+\widehat{\text{ANM}}=180^0\left(\text{2 góc kề bù}\right)\end{matrix}\right.\)
`=>`\(\left\{{}\begin{matrix}\widehat{\text{AMN}}=180^0-114^0=66^0\\\widehat{\text{ANM}}=180^0-130^0=50^0\end{matrix}\right.\)
Xét `\Delta AMN`:
\(\widehat{\text{A}}+\widehat{\text{M}}+\widehat{\text{N}}=180^0\left(\text{định lý tổng 3 góc trong 1 tgiac}\right)\)
`=>`\(\widehat{\text{A}}+66^0+50^0=180^0\)
`=>`\(\widehat{\text{A}}=180^0-66^0-50^0=64^0\)
Mà \(\widehat{\text{A}}=\widehat{\text{x}}\)
`=>`\(\widehat{\text{x}}=64^0\)
Vậy, số đo của góc `x = 64^0.`
Đúng 3
Bình luận (2)
giúp mik vs chỗ nào sai sửa giúp mik vs ạ ;-;
Giúp mik vs ạ, mik đang cần gấp. Mong mng giúp ạ

e: \(E=\dfrac{x^2-9-x^2+4-x^2+9}{\left(x+3\right)\left(x-2\right)}\)
\(=\dfrac{x+2}{x+3}\)
a: \(A=\dfrac{4x^2+x^2-2x+1+x^2+2x+1}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{6x^2+2}{\left(x-1\right)\left(x+1\right)}\)
Đúng 0
Bình luận (1)
\(A=\dfrac{-4x^2+x^2-2x+1-x^2-2x-1}{\left(1-x\right)\left(1+x\right)}=\dfrac{-4x\left(x+1\right)}{\left(1-x\right)\left(1+x\right)}=\dfrac{4x}{x-1}\\ C=\dfrac{-x^2-4x-4+x^2-4x+4-4x^2}{\left(x-2\right)\left(x+2\right)}=\dfrac{-4x\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{4x}{2-x}\\ E=\dfrac{x^2-9-x^2+4x-4-x^2+9}{\left(x-2\right)\left(x+3\right)}=\dfrac{-\left(x-2\right)^2}{\left(x-2\right)\left(x+3\right)}=\dfrac{2-x}{x+3}\)
Đúng 0
Bình luận (0)






