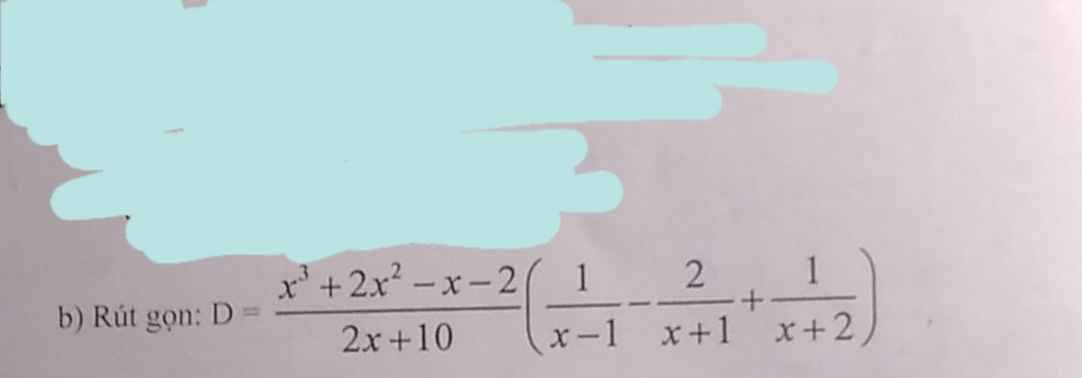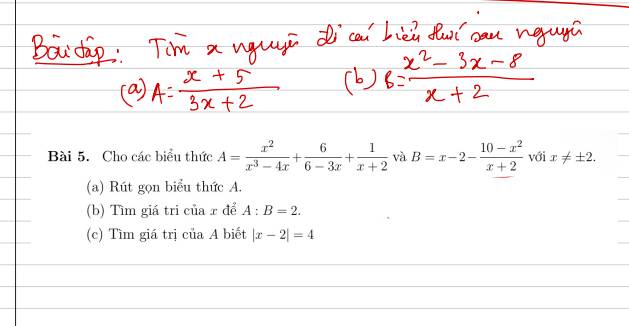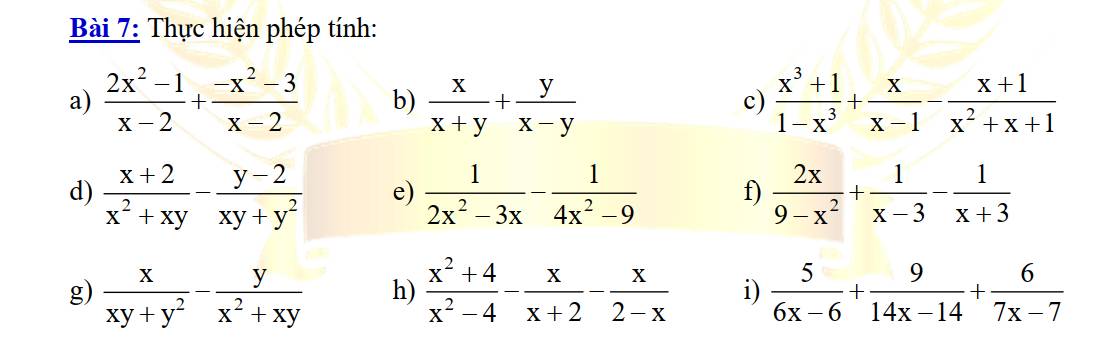Cho biểu thức A =( 3x^2 + 3/x^3-1 - x-1/x^2-x+1 - 1/x-1 ) : 2x^2-5x+5/x-1 a)rút gọn A b)tìm giá trị lớn nhất của A giúp mk vs mk đag cần gấp
Bài 3: Rút gọn phân thức
Bạn nên gõ đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề và hỗ trợ tốt hơn bạn nhé.
Đúng 0
Bình luận (0)
 chi tiết ạ
chi tiết ạ
a) \(P=\dfrac{x^2+2}{x^2+2x-3}:\left(\dfrac{3+x}{3x-3}-\dfrac{1+x}{2x+6}+\dfrac{x^2-27}{6x^2+12x-18}\right)\left(x\ne1;x\ne-3;x\ne\dfrac{1}{2}\right)\)
\(=\dfrac{x^2+2}{\left(x-1\right)\left(x+3\right)}:\left[\dfrac{3+x}{3\left(x-1\right)}-\dfrac{1+x}{2\left(x+3\right)}+\dfrac{x^2-27}{6\left(x^2+2x-3\right)}\right]\)
\(=\dfrac{x^2+2}{\left(x-1\right)\left(x+3\right)}:\left[\dfrac{2\left(x+3\right)^2}{2\cdot3\left(x-1\right)\left(x+3\right)}-\dfrac{3\left(x+1\right)\left(x-1\right)}{3\cdot2\left(x+3\right)\left(x-1\right)}+\dfrac{x^2-27}{6\left(x-1\right)\left(x+3\right)}\right]\)
\(=\dfrac{x^2+2}{\left(x-1\right)\left(x+3\right)}:\dfrac{2\left(x^2+6x+9\right)-3\left(x^2-1\right)+x^2-27}{6\left(x-1\right)\left(x+3\right)}\)
\(=\dfrac{x^2+2}{\left(x-1\right)\left(x+3\right)}:\dfrac{2x^2+12x+18-3x^2+3+x^2-27}{6\left(x-1\right)\left(x+3\right)}\)
\(=\dfrac{x^2+2}{\left(x-1\right)\left(x+3\right)}:\dfrac{12x-6}{6\left(x-1\right)\left(x+3\right)}\)
\(=\dfrac{x^2+2}{\left(x+1\right)\left(x-3\right)}\cdot\dfrac{6\left(x-1\right)\left(x+3\right)}{6\left(2x-1\right)}\)
\(=\dfrac{x^2+2}{2x-1}\)
b) Để \(P\) là số âm thì: \(\dfrac{x^2+2}{2x-1}< 0\)
\(\Rightarrow2x-1< 0\) (vì \(x^2+2>0\))
\(\Leftrightarrow2x< 1\Leftrightarrow x< \dfrac{1}{2}\)
Kết hợp với điều kiên xác định của \(x\), ta được: \(x< \dfrac{1}{2};x\ne-3\)
\(\text{#}Toru\)
Đúng 4
Bình luận (0)
Chi tiết nhất
\(N=\left(\dfrac{3x}{2x-2}-\dfrac{3x}{2x+2}-\dfrac{3x-2}{x^2-1}\right)\cdot\dfrac{4x^2-4}{3}\left(x\ne\pm1\right)\)
\(=\left[\dfrac{3x}{2\left(x-1\right)}-\dfrac{3x}{2\left(x+1\right)}-\dfrac{3x-2}{\left(x-1\right)\left(x+1\right)}\right]\cdot\dfrac{4x^2-4}{3}\)
\(=\left[\dfrac{3x\left(x+1\right)}{2\left(x-1\right)\left(x+1\right)}-\dfrac{3x\left(x-1\right)}{2\left(x-1\right)\left(x+1\right)}-\dfrac{2\cdot\left(3x-2\right)}{2\left(x-1\right)\left(x+1\right)}\right]\cdot\dfrac{4\left(x^2-1\right)}{3}\)
\(=\dfrac{3x^2+3x-3x^2+3x-6x+4}{2\left(x-1\right)\left(x+1\right)}\cdot\dfrac{4\left(x-1\right)\left(x+1\right)}{3}\)
\(=\dfrac{4\cdot2}{3}\)
\(=\dfrac{8}{3}\)
Vậy giá trị của \(N\) không phụ thuộc vào biến \(x\).
Đúng 3
Bình luận (1)
\(N=\left(\dfrac{3x}{2x-2}-\dfrac{3x}{2x+2}-\dfrac{3x-2}{x^2-1}\right)\cdot\dfrac{4x^2-4}{3}\\ =\left(\dfrac{3x}{2\left(x-1\right)}-\dfrac{3x}{2\left(x+1\right)}-\dfrac{3x-2}{\left(x-1\right)\left(x+1\right)}\right)\cdot\dfrac{4x^2-4}{3}\\ =\dfrac{3x\left(x+1\right)-3x\left(x-1\right)-2\left(3x-2\right)}{2\left(x-1\right)\left(x+1\right)}\cdot\dfrac{4x^2-4}{3}\\ =\dfrac{\left(3x^2+3x\right)-\left(3x^2-3x\right)-\left(6x-4\right)}{2\left(x-1\right)\left(x+1\right)}\cdot\dfrac{4x^2-4}{3}\)
\(=\dfrac{3x^2+3x-3x^2+3x-6x+4}{2\left(x-1\right)\left(x+1\right)}\cdot\dfrac{4\left(x-1\right)\left(x+1\right)}{3}\\ =\dfrac{4}{2\left(x-1\right)\left(x+1\right)}\cdot\dfrac{4\left(x-1\right)\left(x+1\right)}{3}\\ =\dfrac{4\cdot2}{3}\)
`=8/3`
`->N` không phụ thuộc vào biến `x`
`color{blue}{ @ A_ri}`
Đúng 2
Bình luận (0)
Chi tiết nhất ah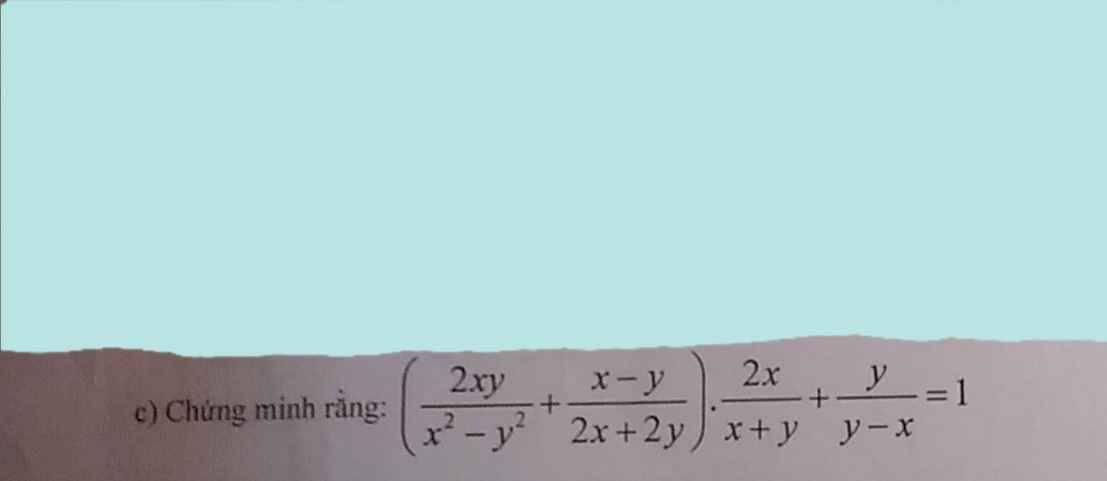
ĐKXĐ: \(x\ne\pm y\)
VT=\(\left(\dfrac{2xy}{x^2-y^2}+\dfrac{x-y}{2x+2y}\right)\cdot\dfrac{2x}{x+y}+\dfrac{y}{y-x}\)
\(=\left(\dfrac{2xy}{\left(x-y\right)\left(x+y\right)}+\dfrac{x-y}{2\left(x+y\right)}\right)\cdot\dfrac{2x}{x+y}-\dfrac{y}{x-y}\)
\(=\dfrac{4xy+\left(x-y\right)^2}{2\left(x-y\right)\left(x+y\right)}\cdot\dfrac{2x}{x+y}-\dfrac{y}{x-y}\)
\(=\dfrac{\left(x+y\right)^2\cdot x}{\left(x-y\right)\cdot\left(x+y\right)^2}-\dfrac{y}{x-y}\)
\(=\dfrac{x}{x-y}-\dfrac{y}{x-y}=\dfrac{x-y}{x-y}=1\)=VP
Đúng 2
Bình luận (0)
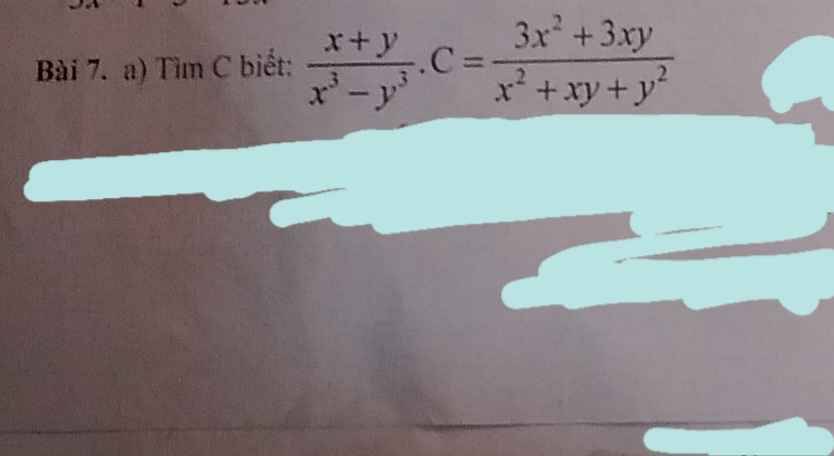 chi tiết nhnhânhất
chi tiết nhnhânhất
ĐKXĐ: \(x\ne\pm y\)
\(\dfrac{x+y}{x^3-y^3}\cdot C=\dfrac{3x^2+3xy}{x^2+xy+y^2}\)
=>\(C=\dfrac{3x^2+3xy}{x^2+xy+y^2}:\dfrac{x+y}{x^3-y^3}\)
=>\(C=\dfrac{3x\left(x+y\right)}{x^2+xy+y^2}\cdot\dfrac{\left(x-y\right)\left(x^2+xy+y^2\right)}{x+y}\)
=>C=3x(x-y)=3x2-3xy
Đúng 2
Bình luận (0)
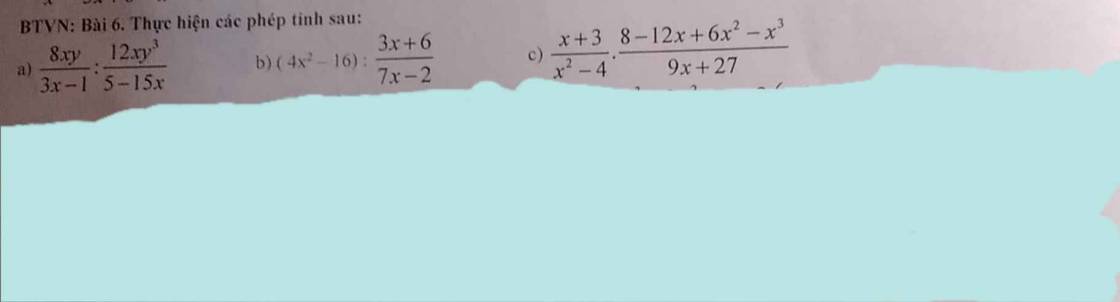 cch tiết nhata
cch tiết nhata
a: ĐKXĐ: \(\left\{{}\begin{matrix}y\ne0\\x\notin\left\{\dfrac{1}{3};0\right\}\end{matrix}\right.\)
\(\dfrac{8xy}{3x-1}:\dfrac{12xy^3}{5-15x}\)
\(=\dfrac{8xy}{3x-1}\cdot\dfrac{-15x+5}{12xy^3}\)
\(=-\dfrac{8xy}{12xy^3}\cdot\dfrac{15x-5}{3x-1}\)
\(=\dfrac{-2}{3y^2}\cdot5=-\dfrac{10}{3y^2}\)
b: ĐKXĐ: \(x\notin\left\{-2;2;\dfrac{2}{7}\right\}\)
\(\left(4x^2-16\right):\dfrac{3x+6}{7x-2}\)
\(=4\left(x^2-4\right)\cdot\dfrac{7x-2}{3\left(x+2\right)}\)
\(=\dfrac{4\left(x-2\right)\left(x+2\right)\cdot\left(7x-2\right)}{3\left(x+2\right)}\)
\(=\dfrac{4\left(x-2\right)\left(7x-2\right)}{3}\)
c: ĐKXĐ: \(x\notin\left\{-3;2;-2\right\}\)
\(\dfrac{x+3}{x^2-4}\cdot\dfrac{8-12x+6x^2-x^3}{9x+27}\)
\(=\dfrac{x+3}{9x+27}\cdot\dfrac{-x^3+6x^2-12x+8}{x^2-4}\)
\(=\dfrac{x+3}{9\left(x+3\right)}\cdot\dfrac{-\left(x-2\right)^3}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{1}{9}\cdot\dfrac{-\left(x-2\right)^2}{x+2}=\dfrac{-\left(x-2\right)^2}{9\left(x+2\right)}\)
Đúng 2
Bình luận (0)
ĐKXĐ: \(x\notin\left\{-5;1;-1;-2\right\}\)
\(D=\dfrac{x^3+2x^2-x-2}{2x+10}\cdot\left(\dfrac{1}{x-1}-\dfrac{2}{x+1}+\dfrac{1}{x+2}\right)\)
\(=\dfrac{x^2\left(x+2\right)-\left(x+2\right)}{2\left(x+5\right)}\cdot\dfrac{\left(x+1\right)\left(x+2\right)-\left(x-1\right)\left(x+2\right)+\left(x-1\right)\left(x+1\right)}{\left(x-1\right)\left(x+1\right)\left(x+2\right)}\)
\(=\dfrac{\left(x+2\right)\left(x^2-1\right)}{2\left(x+5\right)}\cdot\dfrac{x^2+3x+2-\left(x^2+x-2\right)+x^2-1}{\left(x-1\right)\left(x+1\right)\cdot\left(x+2\right)}\)
\(=\dfrac{2x^2+3x+1-x^2-x+2}{2\left(x+5\right)}\)
\(=\dfrac{2x^2+2x+3}{2\left(x+5\right)}\)
Đúng 2
Bình luận (0)
a: ĐKXĐ: x<>2
\(\dfrac{2x^2-1}{x-2}+\dfrac{-x^2-3}{x-2}\)
\(=\dfrac{2x^2-1-x^2-3}{x-2}\)
\(=\dfrac{x^2-4}{x-2}=\dfrac{\left(x-2\right)\left(x+2\right)}{x-2}=x+2\)
b: ĐKXĐ: \(x\ne\pm y\)
\(\dfrac{x}{x+y}+\dfrac{y}{x-y}\)
\(=\dfrac{x\left(x-y\right)+y\left(x+y\right)}{\left(x+y\right)\left(x-y\right)}\)
\(=\dfrac{x^2-xy+xy+y^2}{x^2-y^2}=\dfrac{x^2+y^2}{x^2-y^2}\)
c: ĐKXĐ: x<>1
\(\dfrac{x^3+1}{1-x^3}+\dfrac{x}{x-1}-\dfrac{x+1}{x^2+x+1}\)
\(=\dfrac{-x^3-1}{\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{x}{x-1}-\dfrac{x+1}{x^2+x+1}\)
\(=\dfrac{-x^3-1+x\left(x^2+x+1\right)-\left(x+1\right)\cdot\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{-x^3-1+x^3+x^2+x-x^2+1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x}{x^3-1}\)
d: ĐKXĐ: x<>0; y<>0; x<>-y
\(\dfrac{x+2}{x^2+xy}-\dfrac{y-2}{xy+y^2}\)
\(=\dfrac{x+2}{x\left(x+y\right)}-\dfrac{y-2}{y\left(x+y\right)}\)
\(=\dfrac{y\left(x+2\right)-x\left(y-2\right)}{xy\left(x+y\right)}\)
\(=\dfrac{xy+2y-xy+2x}{xy\left(x+y\right)}=\dfrac{2\left(x+y\right)}{xy\left(x+y\right)}=\dfrac{2}{xy}\)
e: ĐKXĐ: \(x\notin\left\{0;\dfrac{3}{2};-\dfrac{3}{2}\right\}\)
\(\dfrac{1}{2x^2-3x}-\dfrac{1}{4x^2-9}\)
\(=\dfrac{1}{x\left(2x-3\right)}-\dfrac{1}{\left(2x-3\right)\left(2x+3\right)}\)
\(=\dfrac{2x+3-x}{x\left(2x-3\right)\left(2x+3\right)}=\dfrac{x+3}{x\left(2x-3\right)\left(2x+3\right)}\)
f: ĐKXĐ: \(x\notin\left\{3;-3\right\}\)
\(\dfrac{2x}{9-x^2}+\dfrac{1}{x-3}-\dfrac{1}{x+3}\)
\(=\dfrac{-2x}{\left(x-3\right)\left(x+3\right)}+\dfrac{1}{x-3}-\dfrac{1}{x+3}\)
\(=\dfrac{-2x+x+3-x+3}{\left(x-3\right)\left(x+3\right)}=\dfrac{-2x+6}{\left(x-3\right)\left(x+3\right)}=-\dfrac{2}{x+3}\)
g:
ĐKXĐ: x<>0; y<>0; x<>-y
\(\dfrac{x}{xy+y^2}-\dfrac{y}{x^2+xy}\)
\(=\dfrac{x}{y\left(x+y\right)}-\dfrac{y}{x\left(x+y\right)}\)
\(=\dfrac{x^2-y^2}{xy\left(x+y\right)}=\dfrac{\left(x-y\right)\left(x+y\right)}{xy\left(x+y\right)}=\dfrac{x-y}{xy}\)
h: ĐKXĐ: \(x\notin\left\{2;-2\right\}\)
\(\dfrac{x^2+4}{x^2-4}-\dfrac{x}{x+2}-\dfrac{x}{2-x}\)
\(=\dfrac{x^2+4}{\left(x-2\right)\left(x+2\right)}-\dfrac{x}{x+2}+\dfrac{x}{x-2}\)
\(=\dfrac{x^2+4-x\left(x-2\right)+x\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x^2+4-x^2+2x+x^2+2x}{\left(x-2\right)\left(x+2\right)}=\dfrac{x^2+4x+4}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{\left(x+2\right)^2}{\left(x-2\right)\left(x+2\right)}=\dfrac{x+2}{x-2}\)
i: ĐKXĐ: x<>1
\(\dfrac{5}{6x-6}+\dfrac{9}{14x-14}+\dfrac{6}{7x-7}\)
\(=\dfrac{5}{6\left(x-1\right)}+\dfrac{9}{14\left(x-1\right)}+\dfrac{6}{7\left(x-1\right)}\)
\(=\dfrac{1}{x-1}\left(\dfrac{5}{6}+\dfrac{9}{14}+\dfrac{6}{7}\right)\)
\(=\dfrac{1}{x-1}\cdot\left(\dfrac{35}{42}+\dfrac{27}{42}+\dfrac{36}{42}\right)\)
\(=\dfrac{1}{x-1}\cdot\dfrac{98}{42}=\dfrac{7}{3\left(x-1\right)}\)
Đúng 5
Bình luận (0)
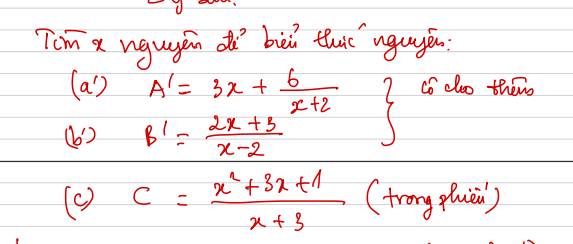
Câu c thôi aa
Lời giải:
$C=\frac{x^2+3x+1}{x+3}=\frac{x(x+3)+1}{x+3}=x+\frac{1}{x+3}$
Với $x$ nguyên, để $C$ nguyên thì $\frac{1}{x+3}$ nguyên.
Với $x$ nguyên, để $\frac{1}{x+3}$ nguyên thì $x+3$ là ước của 1.
$\Rightarrow x+3\in \left\{1; -1\right\}$
$\Rightarrow x\in \left\{-2; -4\right\}$
Đúng 0
Bình luận (0)