Thầy cô và các bạn hỗ trợ em bài này ạ. 
NT
Những câu hỏi liên quan
Các bạn và thầy cô hỗ trợ cho mình câu này ạ.
a, - Thay m = 2 vào phương trình ta được :\(x+2\sqrt{x-1}-3=0\)
\(\Leftrightarrow2\sqrt{x-1}=3-x\)
\(\Leftrightarrow4\left(x-1\right)=x^2-6x+9\left(x\le3\right)\)
\(\Leftrightarrow4x-4=x^2-6x+9\)
\(\Leftrightarrow x^2-10x+13=0\)
\(\Leftrightarrow\)\(x=5\pm2\sqrt{3}\) ( TM )
b, Ta có : \(x+2\sqrt{x-1}-m^2+6m-11=0\)
\(\Leftrightarrow x-1+2\sqrt{x-1}+1-m^2+6m-11=0\)
\(\Leftrightarrow\left(\sqrt{x-1}-1\right)^2=m^2-6m+9+2=\left(m-3\right)^2+2\)
\(\Leftrightarrow\sqrt{x-1}-1=\pm\sqrt{\left(m-3\right)^2+2}\)
\(\Leftrightarrow\sqrt{x-1}=1\pm\sqrt{\left(m-3\right)^2+2}\)
\(\Leftrightarrow x=\left(1\pm\sqrt{\left(m-3\right)^2+2}\right)^2+1\ge1\) ( TM )
=> ĐPCM
Đúng 1
Bình luận (1)
a) Thay \(m=2\) vào phương trình
\(\Rightarrow x+2\sqrt{x-1}-3=0\)
\(\Leftrightarrow2\sqrt{x-1}=3-x\) \(\left(3\ge x\ge1\right)\)
\(\Rightarrow4x-4=9-6x+x^2\)
\(\Leftrightarrow x^2-10x+13=0\) \(\Leftrightarrow\left[{}\begin{matrix}x=5+2\sqrt{3}\left(loại\right)\\x=5-2\sqrt{3}\end{matrix}\right.\)
Vậy ...
b) Đặt \(\sqrt{x-1}=a\) \(\left(a\ge0\right)\)
\(\Rightarrow a^2+2a-m^2+6m-10=0\)
Ta có: \(\Delta'=m^2-6m+11\ge0\forall m\)
Vậy phương trình luôn có nghiệm với mọi m
Đúng 3
Bình luận (0)
a, - Thay m = 2 vào phương trình ta được :
( TM )
b, Ta có :
Đúng 0
Bình luận (0)
Em xin phép nhờ quý thầy cô hỗ trợ cho em bài này với ạ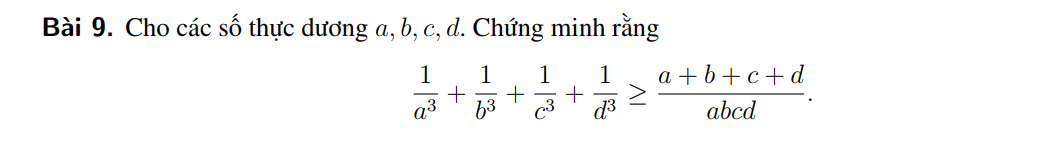
Thực hiện lần lượt BĐT cô-si 3 số cho từng bộ 3 vế trái, ví dụ:
\(\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{1}{c^3}\ge3\sqrt[3]{\dfrac{1}{a^3b^3c^3}}=\dfrac{3}{abc}\)
Làm tương tự, sau đó cộng vế và quy đồng vế phải là sẽ được BĐT cần chứng minh
Đúng 1
Bình luận (0)
Em xin phép nhờ quý thầy cô hỗ trợ giúp em bài này với ạ
Tổng của các số tròn chục nhỏ hơn 90
CÁc số tròn chục nhỏ hơn 90 là :
10 ; 20 ; 30 ; 40 ; 50 ; 60 ; 70 ; 80
Tổng của các số tròn chục nhỏ hơn 90 là :
10 + 20 + ... + 80 = ( 80 + 10 ) x 8 : 2
= 90 x 8 : 2 = 720 : 2 = 360
Tìm tất cả các số nguyên tố \(p\) sao cho \(8.p^2+1\) là số nguyên tố
P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán hỗ trợ giúp đỡ em với ạ!
Em cám ơn nhiều ạ!
Với p = 2 => 8p2 +1 = 33 (loại)
Với p = 3 => 8p2 + 1 = 73 (tm)
Với p > 3 => Đặt p = 3k + 1 ; p = 3k + 2 (k \(\in Z^+\))
Với p = 3k + 1 => 8p2 + 1 = 8(3k + 1)2 + 1
= 72k2 + 48k + 9 = 3(24k2 + 16k + 3) \(⋮3\)(loại)
Với p = 3k + 2 => 8p2 + 1 = 8(3k + 2)2 + 1
= 72k2 + 96k + 33 = 3(24k2 + 32k + 11) \(⋮3\)(loại)
Vậy p = 3 thì 8p2 + 1 \(\in P\)
Đúng 1
Bình luận (1)
- Với \(p=2\) ko thỏa mãn
- Với \(p=3\Rightarrow8p^2+1=73\) là số nguyên tố (thỏa mãn)
- Với \(p>3\Rightarrow p^2\equiv1\left(mod3\right)\)
\(\Rightarrow p^2=3k+1\)
\(\Rightarrow8p^2+1=8\left(3k+1\right)+1=24k+9=3\left(8k+3\right)\) là số lớn hơn 3 và chia hết cho 3
\(\Rightarrow8p^2+1\) là hợp số (ktm)
Vậy \(p=3\) là SNT duy nhất thỏa mãn yêu cầu
Đúng 2
Bình luận (1)
Tìm ba số nguyên tố \(p;q;r\) thỏa mãn : \(p^2+q^2+r^2=5054\)
P/s: Em nhờ quý thầy cô giáo và các bạn yêu toán hỗ trợ giúp đỡ em tham khảo với ạ!
Em cám ơn nhiều lắm ạ!
Nếu p;q;r đều lẻ hoặc có đúng 1 số trong 3 số là lẻ \(\Rightarrow p^2+q^2+r^2\) lẻ, trong khi 5054 chẵn (ktm)
\(\Rightarrow\) Cả p;q;r đều chẵn (loại do \(2^2+2^2+2^2< 5054\)) hoặc có đúng 1 số trong 3 số là chẵn
Do vai trò 3 số như nhau, ko mất tính tổng quát, giả sử r chẵn \(\Rightarrow r=2\)
\(\Rightarrow p^2+q^2=5050\)
Nếu p; q đều chia hết cho 3 \(\Rightarrow p=q=3\Rightarrow ktm\)
Nếu p;q đều ko chia hết cho 3 \(\Rightarrow p^2\) và \(q^2\) đều chia 3 dư 1
\(\Rightarrow p^2+q^2\) chia 3 dư 2 trong khi \(5050\) chia 3 dư 1 (ktm)
\(\Rightarrow\) Có đúng 1 số trong p; q chia hết cho 3, ko mất tính tổng quát, giả sử là p \(\Rightarrow p=3\)
\(\Rightarrow q^2=5050-9=5041\Rightarrow q=71\) là SNT (thỏa mãn)
Vậy bộ 3 số nguyên tố thỏa mãn là \(\left(2;3;71\right)\) và các hoán vị
Đúng 1
Bình luận (1)
Vì tổng của p2 + q2 + r2 \(⋮2\)
=> \(\left[{}\begin{matrix}p⋮2\\q⋮2\\r⋮2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}p=2\\q=2\\r=2\end{matrix}\right.\);
Giả sử r = 2 => p2 + q2 = 5050 ; p;q lẻ
=> Chữ số tận cùng p2 chỉ có thể là 9;1
=> Chư số tận cùng p là 1;3;7;9
mà p2 + q2 = 5050 => q2 \(< 5050\) ; p2 < 5050
<=> q < 72 (1) ; p < 72 (2)
Lại có p2 + q2 = 5050
<=> 2pq = 5050 - (p - q)2 < 5050
<=> pq \(< 2525\) (3)
Từ (1) ; (3) => p > 35 (4)
Từ (2) ; (4) => 35 < p < 72
<=> p \(\in\left\{37;41;43;47;53;59;61;67;71\right\}\)
Thử từng giá trị p => tìm được p = 71 thỏa mán
thay vào pt gốc được q = 3 (tm)
Vậy các cặp (p;q;r) thỏa là (71;3;2) và các hoán vị
Đúng 0
Bình luận (0)
Giả sử p<q<r.
Số 2 là số nguyên tố chẵn duy nhất.
Số lẻ có dạng 2k+1 (k\(\in\)N), bình phương của số lẻ là (2k+1)2=4k2+4k+1 là một số lẻ.
Mà p2+q2+r2 là một số chẵn (=5054), suy ra p=2.
q2+r2=5050 \(\Rightarrow\) q2<2525 \(\Rightarrow\) 3\(\le\)q<50.
Với q=3 \(\Rightarrow\) r=71 (nhận).
Vậy ba số nguyên tố cần tìm là 2, 3 và 71.
Đúng 1
Bình luận (0)
Tìm tất cả các số nguyên dương \(n\) sao cho biểu thức sau \(P=n^3+7n^2+25n+39\) nhận giá trị là lũy thừa của một số nguyên tố?
P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán gợi ý và hỗ trợ em bài toán số học, em tham khảo với ạ!
Em cám ơn nhiều lắm ạ!
\(P=n^3+7n^2+25n+39=\left(n+3\right)\left(n^2+4n+13\right)\)
Hiển nhiên \(\left\{{}\begin{matrix}n+3>1\\n^2+4n+13>1\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}n+3=p^a\\n^2+4n+13=p^b\end{matrix}\right.\) với \(b>a>0\)
\(\Rightarrow\left\{{}\begin{matrix}n+3⋮p\\n^2+4n+13⋮p\end{matrix}\right.\) \(\Rightarrow n^2+4n+13-\left(n+3\right)\left(n+1\right)⋮p\)
\(\Rightarrow10⋮p\Rightarrow\left[{}\begin{matrix}p=2\\p=5\end{matrix}\right.\)
- TH1: \(p=2\Rightarrow n+3=2^a\)
Do n nguyên dương \(\Rightarrow n+3\ge4\Rightarrow a\ge2\Rightarrow2^a⋮4\)
\(\Rightarrow n+3⋮4\Rightarrow n=4k+1\)
Đồng thời \(n^2+4n+13=2^b\), hiển nhiên \(b>2\Rightarrow n^2+4n+13⋮4\)
\(\Rightarrow\left(4k+1\right)^2+4\left(4k+1\right)+13⋮4\)
\(\Rightarrow4k\left(4k+6\right)+18⋮4\) (vô lý)
\(\Rightarrow p=2\) không thỏa mãn
TH2: \(p=5\) \(\Rightarrow\left\{{}\begin{matrix}n+3=5^a\\n^2+4n+13=5^b\end{matrix}\right.\)
\(\Rightarrow\left(n+1\right)\left(n+3\right)+10=5^b\)
\(\Rightarrow5^a\left(5^a-2\right)+10=5^b\)
\(\Rightarrow5^{a-1}\left(5^a-2\right)+2=5^{b-1}\)
- Với \(a=1\Rightarrow b=2\)
- Với \(a>1\Rightarrow\) vế trái chia 5 dư 2, vế phải chia hết cho 5
\(\Rightarrow\) Không tồn tại a;b nguyên thỏa mãn
Vậy \(a=1\Rightarrow n=5^1-3=2\)
Đúng 3
Bình luận (0)
Cho \(x;y\) là các số thực thỏa mãn : \(5x^2+2xy+2y^2=9\).
Tìm giá trị nhỏ nhất của biểu thức \(P=\dfrac{x-1`}{4x-y-9}\).
P/s: Em xin phép nhờ quý thầy cô giáo và các bạn hỗ trợ giúp đỡ với ạ!
Em cám ơn nhiều ạ!
Em xin phép nhờ quý thầy cô và các bạn giúp đỡ với ạ!
Đúng 0
Bình luận (0)
Chứng minh rằng với mọi số nguyên dương \(n\) thì \(n^4+4.n^3+7.n^2+6n+3\) luôn luôn không là số lập phương .
P/s: em in phép nhờ quý thầy cô giáo và các bạn trong nhóm hỗ trợ và giúp đỡ em tham khảo với ạ, em cám ơn nhiều ạ!
Đặt \(N=n^4+4n^3+7n^2+6n+3=\left(n^2+n+1\right)\left(n^2+3n+3\right)\)
Do \(n\) và \(n+1\) luôn khác tính chẵn lẻ \(\Rightarrow n^2\) và \(n+1\) khác tính chẵn lẻ
\(\Rightarrow n^2+n+1\) luôn lẻ
Gọi \(d=ƯC\left(n^2+n+1;n^2+3n+3\right)\) \(\Rightarrow d\) lẻ
\(\Rightarrow n^2+3n+3-\left(n^2+n+1\right)⋮d\)
\(\Rightarrow2\left(n+1\right)⋮d\)
\(\Rightarrow n+1⋮d\)
\(\Rightarrow\left(n+1\right)^2⋮d\Rightarrow\left(n+1\right)^2-\left(n^2+n+1\right)⋮d\)
\(\Rightarrow n⋮d\Rightarrow n+1-n⋮d\Rightarrow d=1\)
\(\Rightarrow n^2+n+1\) và \(n^2+3n+3\) nguyên tố cùng nhau
Giả sử tồn tại m nguyên dương thỏa mãn: \(\left(n^2+n+1\right)\left(n^2+3n+3\right)=m^3\)
Hiển nhiên \(m>1\), do \(n^2+n+1\) và \(n^2+3n+3\) nguyên tố cùng nhau, đồng thời \(n^2+3n+3>n^2+n+1\)
\(\Rightarrow\left\{{}\begin{matrix}n^2+n+1=1\\n^2+3n+3=m^3\end{matrix}\right.\)
Từ \(n^2+n+1=1\Rightarrow\left[{}\begin{matrix}n=-1\\n=0\end{matrix}\right.\) đều ko thỏa mãn n nguyên dương
Vậy N luôn luôn ko là lập phương
Đúng 1
Bình luận (1)
Chứng minh rằng với mọi số nguyên dương n thì \(n.\left(n+1\right).\left(n+2\right).\left(n+3\right)\) luôn luôn không thể là số lập phương.
P/S: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán hỗ trợ giúp đỡ em với ạ!
Em cám ơn nhiều lắm ạ!
lập phương hay chính phương thế bạn???
Đúng 1
Bình luận (1)
nếu là chính phương thì ntn nha
\(n\left(n+1\right)\left(n+2\right)\left(n+3\right)=\left(n^2+3n\right)\left(n^2+3n+2\right)\)
đặt \(t=n^2+3n\left(t\in Z^+\right)\)
phương trình thành:
\(t\left(t+2\right)=t^2+2t\)
vì \(t^2< t^2+2t< t^2+2t+1\)
hay \(t^2< t^2+2t< \left(t+1\right)^2\)
=> \(t^2+2t\) không thể là số chính phương
=>\(n\left(n+2\right)\left(n+2\right)\left(n+3\right)\) luôn luôn không thể là số chính phương
Đúng 1
Bình luận (0)
cô ơi, cô là người hay cô là chó vậy ạ ?, bài tập thầy con soạn bao nhiêu công sức cô ăn cắp như con chó không thèm ghi nguồn rồi đăng lên đây, thầy con đã nói rồi mà cô vẫn cố tình nhai đi nhai lại mấy tháng nay, bẩn không bằng con chó cô ạ, cô làm như vậy là báo hại đến học sinh bọn con thôi ạ, cô làm ơn bỏ cái trò đó đi ạ
Đúng 0
Bình luận (0)






