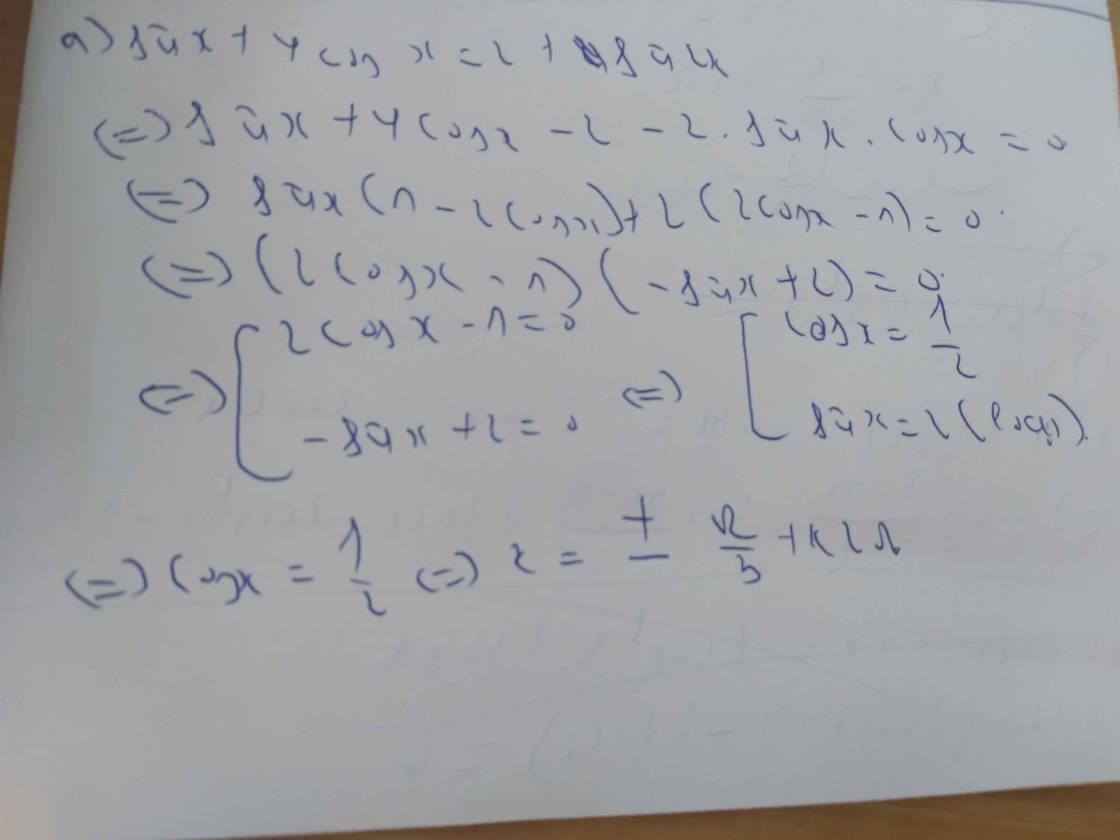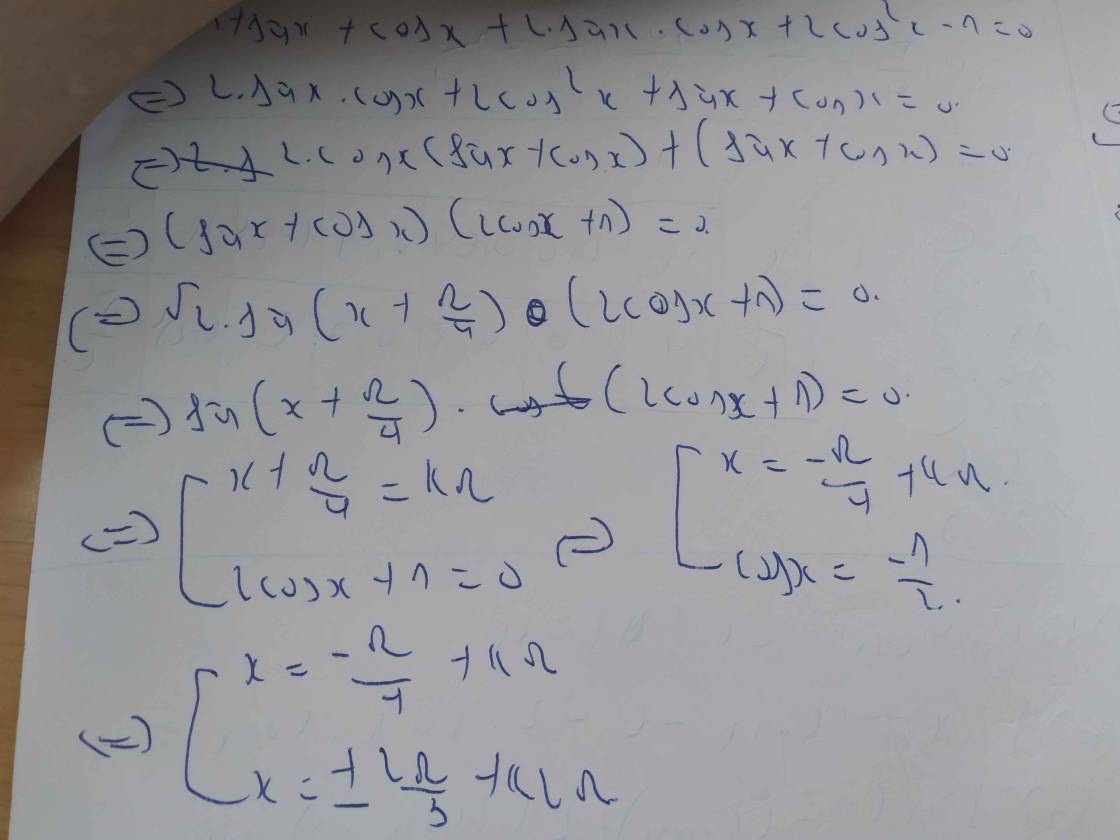\(\dfrac{cos2x-sinx-cosx+2}{sinx-1}=0\)
TD
Những câu hỏi liên quan
\(sinx+4cosx=2+sin2x\)
\(\left(1-sin2x\right)\left(sinx+cosx\right)=cos2x\)
\(1+sinx+cosx+sin2x+cos2x=0\)
\(sinx+sin2x+sin3x=1+cosx+cos2x\)
\(sin^22x-cos^28x=sin\left(\dfrac{17\pi}{2}+10x\right)\)
1> 1 + sinx + cosx + sin2x + cos2x = 0
2> cos2x + 3sin2x + 5 sinx - 3cosx = 3
3> \(\dfrac{\sqrt{2}*(cosx - sinx)}{cotx - 1}\) = \(\dfrac{1}{tanx + cot2x}\)
4> (2cosx - 1)*(2sinx + cosx) = sin2x - sinx
Giải pt
\(2sin\left(x+\dfrac{\pi}{6}\right)+sinx+2cosx=3\)
\(\left(sin2x+cos2x\right)cosx+2cos2x-sinx=0\)
\(sin2x-cos2x+3sinx-cosx-1=0\)
1.
\(2sin\left(x+\dfrac{\pi}{6}\right)+sinx+2cosx=3\)
\(\Leftrightarrow\sqrt{3}sinx+cosx+sinx+2cosx=3\)
\(\Leftrightarrow\left(\sqrt{3}+1\right)sinx+3cosx=3\)
\(\Leftrightarrow\sqrt{13+2\sqrt{3}}\left[\dfrac{\sqrt{3}+1}{\sqrt{13+2\sqrt{3}}}sinx+\dfrac{3}{\sqrt{13+2\sqrt{3}}}cosx\right]=3\)
Đặt \(\alpha=arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}\)
\(pt\Leftrightarrow\sqrt{13+2\sqrt{3}}sin\left(x+\alpha\right)=3\)
\(\Leftrightarrow sin\left(x+\alpha\right)=\dfrac{3}{\sqrt{13+2\sqrt{3}}}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\alpha=arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\\x+\alpha=\pi-arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\pi-2arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\end{matrix}\right.\)
Vậy phương trình đã cho có nghiệm:
\(x=k2\pi;x=\pi-2arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\)
Đúng 0
Bình luận (0)
2.
\(\left(sin2x+cos2x\right)cosx+2cos2x-sinx=0\)
\(\Leftrightarrow2sinx.cos^2x+cos2x.cosx+2cos2x-sinx=0\)
\(\Leftrightarrow\left(2cos^2x-1\right)sinx+cos2x.cosx+2cos2x=0\)
\(\Leftrightarrow cos2x.sinx+cos2x.cosx+2cos2x=0\)
\(\Leftrightarrow cos2x.\left(sinx+cosx+2\right)=0\)
\(\Leftrightarrow cos2x=0\)
\(\Leftrightarrow2x=\dfrac{\pi}{2}+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
Vậy phương trình đã cho có nghiệm \(x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
Đúng 0
Bình luận (0)
Giải phương trình:
a, \(Tanx+Cosx-Cos^2x=Sinx\left(1+Tanx.Tan\dfrac{x}{2}\right)\)
b, \(1+Sinx+Cosx+Sin2x+Cos2x=0\)
1 + sinx + cosx + sin2x + cos2x = 0
<=> sin^2x+ cos^2 x + ( sinx+cosx) + 2.sinx.cosx + ( cos^2 x - sin^2 x)=0
<=> 2 cos^2 x + 2sinx.cosx + sinx + cosx =0
<=> 2cosx ( cos x + sinx) + sinx + cosx = 0
<=> ( cosx + sinx ) (2 cos x + 1 ) = 0
<=> cosx + sinx = 0 hoặc 2cosx + 1 =0
Đúng 1
Bình luận (0)
Giải các pt sau
a, \(\dfrac{1}{sinx}+\dfrac{1}{cosx}=4sin\left(x+\dfrac{\pi}{4}\right)\)
b, \(2sin\left(2x-\dfrac{\pi}{6}\right)+4sinx+1=0\)
c, \(cos2x+\sqrt{3}sinx+\sqrt{3}sin2x-cosx=2\)
d, \(4sin^2\dfrac{x}{2}-\sqrt{3}cos2x=1+cos^2\left(x-\dfrac{3\pi}{4}\right)\)
1. Cho sinx dfrac{2}{3} , x ∈ (0,dfrac{Pi}{2})Tính cosx, tanx , sin (x+dfrac{Pi}{4})2. Cho cos dfrac{1}{4} . Tính sinx, cos2x3. Cho tanx 2 . Tính cosx, sinxx ∈ (0,dfrac{Pi}{2})4. Rút gọn a) A cos2x - 2cos2x + sinx +1 b) B dfrac{cos3x+cos2x+cosx}{cos2x}
Đọc tiếp
1. Cho sinx = \(\dfrac{2}{3}\) , x ∈ (0,\(\dfrac{\Pi}{2}\))
Tính cosx, tanx , sin (x+\(\dfrac{\Pi}{4}\))
2. Cho cos = \(\dfrac{1}{4}\) . Tính sinx, cos2x
3. Cho tanx = 2 . Tính cosx, sinx
x ∈ (0,\(\dfrac{\Pi}{2}\))
4. Rút gọn a) A = cos2x - 2cos2x + sinx +1
b) B = \(\dfrac{cos3x+cos2x+cosx}{cos2x}\)
1.
\(0< x< \dfrac{\pi}{2}\Rightarrow cosx>0\)
\(\Rightarrow cosx=\sqrt{1-sin^2x}=\dfrac{\sqrt{5}}{3}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{2}{\sqrt{5}}\)
\(sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\left(sinx+cosx\right)=\dfrac{\sqrt{10}+2\sqrt{2}}{6}\)
2.
Đề bài thiếu, cos?x
Và x thuộc khoảng nào?
3.
\(x\in\left(0;\dfrac{\pi}{2}\right)\Rightarrow sinx;cosx>0\)
\(\dfrac{1}{cos^2x}=1+tan^2x=5\Rightarrow cos^2x=\dfrac{1}{5}\Rightarrow cosx=\dfrac{\sqrt{5}}{5}\)
\(sinx=cosx.tanx=\dfrac{2\sqrt{5}}{5}\)
4.
\(A=\left(2cos^2x-1\right)-2cos^2x+sinx+1=sinx\)
\(B=\dfrac{cos3x+cosx+cos2x}{cos2x}=\dfrac{2cos2x.cosx+cos2x}{cos2x}=\dfrac{cos2x\left(2cosx+1\right)}{cos2x}=2cosx+1\)
Đúng 2
Bình luận (0)
1) cosx\(^2\)+sinx=0
2) 2cos\(^2\)x-cos2x+cosx=0
3) sin\(^2\)x-3cos2x-2=0
4) tanx+\(\dfrac{2}{cotx}\)=0
3.
\(\dfrac{1}{2}-\dfrac{1}{2}cos2x-3cos2x-2=0\)
\(\Leftrightarrow-7cos2x-3=0\)
\(\Rightarrow cos2x=-\dfrac{3}{7}\)
\(\Rightarrow2x=\pm arccos\left(-\dfrac{3}{7}\right)+k2\pi\)
\(\Rightarrow x=\pm\dfrac{1}{2}arccos\left(-\dfrac{3}{7}\right)+k\pi\)
4.
ĐKXĐ: \(x\ne\dfrac{k\pi}{2}\)
\(tanx+2tanx=0\)
\(\Rightarrow3tanx=0\)
\(\Rightarrow tanx=0\)
\(\Rightarrow x=k\pi\) (loại do ĐKXĐ)
Vậy pt đã cho vô nghiệm
Đúng 2
Bình luận (0)
1.
\(\Leftrightarrow1-sin^2x+sinx=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{1+\sqrt{5}}{2}>1\left(loại\right)\\sinx=\dfrac{1-\sqrt{5}}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=arcsin\left(\dfrac{1-\sqrt{5}}{2}\right)+k2\pi\\x=\pi-arcsin\left(\dfrac{1-\sqrt{5}}{2}\right)+k2\pi\end{matrix}\right.\) (\(k\in Z\))
2.
\(2cos^2x-\left(2cos^2x-1\right)+cosx=0\)
\(\Leftrightarrow cosx+1=0\)
\(\Leftrightarrow cosx=-1\)
\(\Leftrightarrow x=\pi+k2\pi\) (\(k\in Z\))
Đúng 1
Bình luận (0)
giải các pt sau:
a) cosx(1-cos2x) - sin^2x = 0
b) sin3x + cos2x = 1 + 2sinxcos3x
c) ( cosx+1)(sinx - cosx + 3) = sin^2x
d) (1+sinx)(cosx-sinx) = cos^2x
a.
\(\Leftrightarrow cosx\left[1-\left(1-2sin^2x\right)\right]-sin^2x=0\)
\(\Leftrightarrow2sin^2x.cosx-sin^2x=0\)
\(\Leftrightarrow sin^2x\left(2cosx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\cosx=\frac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\frac{\pi}{3}+k2\pi\\x=-\frac{\pi}{3}+k2\pi\end{matrix}\right.\)
b.
Câu b chắc chắn đề đúng chứ bạn? Vế phải ấy?
Đúng 0
Bình luận (0)
c/
\(\left(1+cosx\right)\left(sinx-cosx+3\right)=1-cos^2x\)
\(\Leftrightarrow\left(1+cosx\right)\left(sinx-cosx+3\right)-\left(1+cosx\right)\left(1-cosx\right)=0\)
\(\Leftrightarrow\left(1+cosx\right)\left(sinx+2\right)=0\)
\(\Leftrightarrow cosx=-1\)
\(\Leftrightarrow x=\pi+k2\pi\)
d.
\(\Leftrightarrow\left(1+sinx\right)\left(cosx-sinx\right)=1-sin^2x\)
\(\Leftrightarrow\left(1+sinx\right)\left(cosx-sinx\right)-\left(1+sinx\right)\left(1-sinx\right)=0\)
\(\Leftrightarrow\left(1+sinx\right)\left(cosx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=-1\\cosx=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\frac{\pi}{2}+k2\pi\\x=k2\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
HELPING NOW!!!
Giair phương trình lượng giác sau:
1) cosx - cos2x +cos3x = 0
2) cos2x - sin2x = sin3x + cos4x
3) cos2x + 2sinx - 1 - 2sinxsosx = 0
4) 1+ sinx - cosx = sin2x - cos2x
5) \(\sqrt{2}\) sin (2x+\(\dfrac{\pi}{4}\)) - sinx - 3cosx +2 =0
6) sin2x + 2cos2x = 1+sinx - 4cosx