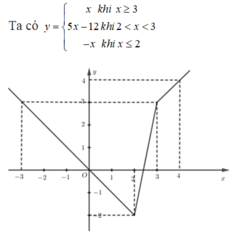
Cho hàm số y=\(x^2-2x-3\). Tìm giá trị lớn nhất của hàm số với \(x\in\left[-3;4\right]\).
PP
Những câu hỏi liên quan
a) Cho hàm số yx^2+2x+3+left|x-a+1right| có bao nhiêu giá trị nguyên của tham số ainleft[-10;10right] sao cho giá trị nhỏ nhất của hàm số lớn hơn 2b) Tìm tất cả các giá trị của tham số m để hệ bất pt left{{}begin{matrix}x^2-2x-3le0x^2-2mx+m^2-9ge0end{matrix}right. có nghiệmc) Gọi (x;y) là nghiệm của hệ bất pt left{{}begin{matrix}x-2y-2le04x-3y+12ge0x+3y+3ge02x+y-4le0end{matrix}right.. Tìm giá trị lớn nhất của biểu thức F4x+5y-6
Đọc tiếp
a) Cho hàm số \(y=x^2+2x+3+\left|x-a+1\right|\) có bao nhiêu giá trị nguyên của tham số \(a\in\left[-10;10\right]\) sao cho giá trị nhỏ nhất của hàm số lớn hơn 2
b) Tìm tất cả các giá trị của tham số m để hệ bất pt \(\left\{{}\begin{matrix}x^2-2x-3\le0\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\) có nghiệm
c) Gọi (x;y) là nghiệm của hệ bất pt \(\left\{{}\begin{matrix}x-2y-2\le0\\4x-3y+12\ge0\\x+3y+3\ge0\\2x+y-4\le0\end{matrix}\right.\). Tìm giá trị lớn nhất của biểu thức F=4x+5y-6
b, \(\left\{{}\begin{matrix}x^2-2x-3\le0\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1\le x\le3\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\)
Yêu cầu bài toán thỏa mãn khi phương trình \(f\left(x\right)=x^2-2mx+m^2-9\ge0\) có nghiệm \(x\in\left[-1;3\right]\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=m^2-m^2+9=9>0,\forall m\\-1< m< 3\\f\left(-1\right)=m^2+2m-8\ge0\\f\left(3\right)=m^2-6m\ge0\end{matrix}\right.\)
\(\Leftrightarrow m\in[2;3)\cup(-1;0]\)
Đúng 0
Bình luận (0)
Cho hàm số \(y=x^2+2x+3+\left|x-a+1\right|\), có bao nhiêu giá trị nguyên của tham số a \(\in\left[-10;10\right]\) sao cho giá trị nhỏ nhất của hàm số lớn hơn 2
Cho hàm số y 3|x − 2| − |2x − 6| có đồ thị (C). Tìm giá trị lớn nhất và nhỏ nhất của hàm số trên với x
∈
[−3; 4] A.
max
−
3
;
4
y
4
B.
min
y
−
2
−
3...
Đọc tiếp
Cho hàm số y = 3|x − 2| − |2x − 6| có đồ thị (C). Tìm giá trị lớn nhất và nhỏ nhất của hàm số trên với x ∈ [−3; 4]
A. max − 3 ; 4 y = 4
B. min y = − 2 − 3 ; 4
C. Cả A, B đều đúng
D. Cả A, B đều sai
Câu 1: Cho hàm số y (3m + 5) x^2 với m ne dfrac{-5}{3}. Tìm các giá trị của tham số m để hàm số:a) Nghịch biến với mọi x 0b) Đồng biến với mọi x 0c) Đạt giá trị lớn nhất là 0d) Đạt giá trị nhỏ nhất là 0Câu 2: Cho hàm số y left(sqrt{3k+4}-3right)x^2 với k gedfrac{-4}{3}; k nedfrac{5}{3} Tính các giá trị của tham số K để hàm số:a) Nghịch biến với mọi x 0b) Đồng biến với mọi x 0
Đọc tiếp
Câu 1: Cho hàm số y = (3m + 5) x\(^2\) với m \(\ne\) \(\dfrac{-5}{3}\). Tìm các giá trị của tham số m để hàm số:
a) Nghịch biến với mọi x > 0
b) Đồng biến với mọi x >0
c) Đạt giá trị lớn nhất là 0
d) Đạt giá trị nhỏ nhất là 0
Câu 2: Cho hàm số y = \(\left(\sqrt{3k+4}-3\right)x^2\) với k \(\ge\dfrac{-4}{3}\); k \(\ne\dfrac{5}{3}\)
Tính các giá trị của tham số K để hàm số:
a) Nghịch biến với mọi x >0
b) Đồng biến với mọi x >0
Câu 1:
a) Để hàm số \(y=\left(3m+5\right)\cdot x^2\) nghịch biến với mọi x>0 thì \(3m+5< 0\)
\(\Leftrightarrow3m< -5\)
hay \(m< -\dfrac{5}{3}\)
Vậy: Để hàm số \(y=\left(3m+5\right)\cdot x^2\) nghịch biến với mọi x>0 thì \(m< -\dfrac{5}{3}\)
b) Để hàm số \(y=\left(3m+5\right)\cdot x^2\) đồng biến với mọi x>0 thì
3m+5>0
\(\Leftrightarrow3m>-5\)
hay \(m>-\dfrac{5}{3}\)
Vậy: Để hàm số \(y=\left(3m+5\right)\cdot x^2\) đồng biến với mọi x>0 thì \(m>-\dfrac{5}{3}\)
Đúng 2
Bình luận (0)
2.
Để hàm nghịch biến với x>0 \(\Leftrightarrow\sqrt{3k+4}-3< 0\)
\(\Leftrightarrow\sqrt{3k+4}< 3\Leftrightarrow3k+4< 9\)
\(\Rightarrow-\dfrac{4}{3}\le k< \dfrac{5}{3}\)
Để hàm đồng biến khi x>0
\(\Leftrightarrow\sqrt{3k+4}-3>0\Leftrightarrow\sqrt{3k+4}>3\)
\(\Leftrightarrow3k+4>9\Rightarrow k>\dfrac{5}{3}\)
Đúng 1
Bình luận (0)
Tìm giá trị lớn nhất của hàm số \(y=x^2-2x+3\) trên đoạn \(\left[0;4\right]\)
\(y=f\left(x\right)=x^2-2x+3\)
\(f\left(0\right)=3;f\left(4\right)=11;f\left(1\right)=2\)
\(\Rightarrow max=f\left(4\right)=11\Leftrightarrow x=4\)
Đúng 1
Bình luận (0)
Cho hàm số y = \(|2x-x^2-\sqrt{\left(x+1\right)\left(3-x\right)}+b|\)Để giá trị lớn nhất của hàm số đạt giá trị nhỏ nhất thì giá trị của b thuộc khoảng nào
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
a) \(y=f\left(x\right)=\dfrac{4}{\sqrt{5-2\cos^2x\sin^2x}}\)
b)\(y=f\left(x\right)=3\sin^2x+5\cos^2x-4\cos2x-2\)
c)\(y=f\left(x\right)=\sin^6x+\cos^6x+2\forall x\in\left[\dfrac{-\pi}{2};\dfrac{\pi}{2}\right]\)
Bài 1: Cho hàm sốyxsqrt{m-1}-dfrac{3}{2}.Tìm giá trị của m sao cho hàm số trên là hàm số bậc nhất
Bài 2: Với giá trị nào của k thì:
a)Hàm số yleft(k^2-5k-6right)x-13 đồng biến?
b)Hàm số yleft(2k^2+3k-2right)x+3 nghịch biến?
Bài 3: Cho hai hàm số bậc nhất y 2x + k và y (2m + 1)x + 2k - 3. Tìm điều kiện đối với m và k để hai đồ thị hàm số là:
a)Hai đường thẳng cắt nhau
b)Hai đường thẳng song song với nhau
c)Hai đường thẳng trùng nhau
Bài 4: Cho đường thẳng (d): y (m - 3)x + 1 - m. Xác đ...
Đọc tiếp
Bài 1: Cho hàm số\(y=x\sqrt{m-1}-\dfrac{3}{2}\).Tìm giá trị của m sao cho hàm số trên là hàm số bậc nhất
Bài 2: Với giá trị nào của k thì:
a)Hàm số \(y=\left(k^2-5k-6\right)x-13\) đồng biến?
b)Hàm số \(y=\left(2k^2+3k-2\right)x+3\) nghịch biến?
Bài 3: Cho hai hàm số bậc nhất y = 2x + k và y = (2m + 1)x + 2k - 3. Tìm điều kiện đối với m và k để hai đồ thị hàm số là:
a)Hai đường thẳng cắt nhau
b)Hai đường thẳng song song với nhau
c)Hai đường thẳng trùng nhau
Bài 4: Cho đường thẳng (d): y = (m - 3)x + 1 - m. Xác định m trong các trường hợp sau đây:
a) (d) cắt trục Ox tại điểm A có hoành độ x = 2
b) (d) cắt trục tung Ox tại điểm B có tung độ y = -3
c) (d) đi qua điểm C(-1 ; 4)
Lập bảng biến thiên của hàm số \(y = {x^2} + 2x + 3.\) Hàm số này có giá trị lớn nhất hay giá trị nhỏ nhất? Tìm giá trị đó.
Tham khảo:
Đỉnh S có tọa độ: \({x_S} = \dfrac{{ - b}}{{2a}} = \dfrac{{ - 2}}{{2.1}} = - 1;\,{y_S} = {\left( { - 1} \right)^2} + 2.( - 1) + 3 = 2.\)
Hay \(S\left( { - 1;2} \right).\)
Vì hàm số bậc hai có \(a = 1 > 0\) nên ta có bảng biến thiên sau:
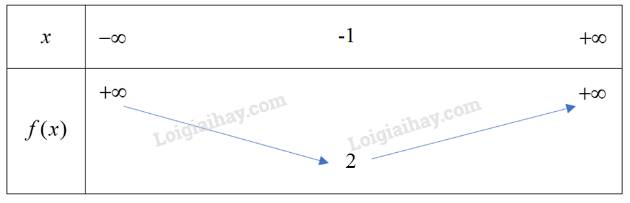
Hàm số đạt giá trị nhỏ nhất bằng \(2\).
Đúng 0
Bình luận (0)