cho đường tròn (O,1cm) và dây AB=1cm. tính khoảng cách từ tâm O đến dây AB
cho đường tròn tâm O bán kính 1cm và dây AB=1cm. khoảng cách từ tâm O đến AB bằng?
cần gấp m.n á giúp em với !
Gọi H là trung điểm AB \(\Rightarrow OH\perp AB\) đồng thời \(AH=\dfrac{AB}{2}=\dfrac{1}{2}\)
\(OH=\sqrt{R^2-AH^2}=\sqrt{1-\dfrac{1}{4}}=\dfrac{\sqrt{3}}{2}\) (cm)
Cho đường tròn tâm O bán kính 5cm, dây AB bằng 8cm.
a) Tính khoảng cách từ tâm O đến dây AB.
b) Gọi I là điểm thuộc dây AB sao cho AI = 1cm. Kẻ dây CD đi qua I và vuông góc với AB. Chứng minh rằng CD = AB.
a) Kẻ OJ vuông góc với AB tại J.
Theo quan hệ vuông góc giữa đường kính và dây suy ra: J là trung điểm của AB.
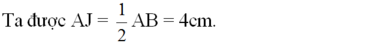
Áp dụng định lí Pitago trong tam giác vuông OAJ có:
OJ2 = OA2 – AJ2 = 52 – 42 = 9 (OA = R = 5cm)
=> OJ = 3cm (1)
Vậy khoảng cách từ tâm O đến dây AB là OJ = 3cm.
b) Kẻ OM vuông góc với CD tại M.
Tứ giác OJIM có: 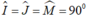 nên là hình chữ nhật
nên là hình chữ nhật
Ta có IJ = AJ – AI = 4 – 1 = 3cm
=> OM = IJ = 3cm (Tính chất hình chữ nhật) (2)
Từ (1), (2) suy ra CD = AB (hai dây cách đều tâm thì bằng nhau). (đpcm)
Cho đường tròn tâm O bán kính 5cm, dây AB bằng 8cm
a) Tính khoảng cách từ tâm O đến dây AB
b) Gọi I là điểm thuộc dây AB sao cho AI = 1cm. Kẻ dây CD đi qua I và vuông góc với AB. Chứng minh rằng CD = AB
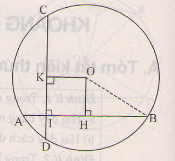
a) Vẽ , ta có HA=HB=4cm.
Xét tam giác HOB vuông tại H, có:
.
b) Vẽ . TỨ giác KOHI có ba góc vuông nên là hình chữ nhật, suy ra OK=HI. Ta có HI=4-1=3cm, suy ra OK=3cm.
Vậy OH=OK=3cm.
Hai dây AB và CD cách đều tâm nên chúng bằng nhau.
Do đó AB=CD.
a) Vẽ OH ⊥ AB, ta có HA=HB=4cm.
Xét tam giác HOB vuông tại H, có:
OH2 = OB2 – HB2 =52 – 42 = 9
⇒ OH = 3(cm).
b) Vẽ OK ⊥ CD. Tứ giác KOHI có ba góc vuông nên là hình chữ nhật, suy ra OK=HI.
Ta có HI=4-1=3cm, suy ra OK=3cm.
Vậy OH=OK=3cm. Hai dây AB và CD cách đều tâm nên chúng bằng nhau.
Do đó AB=CD.
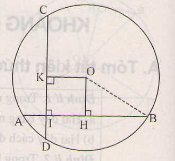
Cho đường tròn tâm O bán kính 5cm , dây AB=8cm.
a/ Tính khoảng cách từ O đến dây AB.
b/ Gọi I là điểm thuộc dây AB sao cho AI=1cm, kẽ dây CD đi qua điểm I và vuông góc AB.C/m CD= AB
a) Kẻ OJ vuông góc với AB tại J.
Theo quan hệ vuông góc giữa đường kính và dây suy ra : J là trung điểm của AB
Ta được : \(AJ=\frac{1}{2}AB=4cm\)
Áp dụng định lí Pitago trong tam giác vuông OAJ có:
OJ2 = OA2 – AJ2 = 52 – 42 = 9 ( OA = R = 5cm )
=> OJ = 3cm (1)
Vậy khoảng cách từ tâm O đến dây AB là OJ = 3cm.
b) Kẻ OM vuông góc với CD tại M.
Tứ giác OJIM có :\(\widehat{I}=\widehat{J}=\widehat{M}=90^o\)nên là hcn
Ta có IJ = AJ – AI = 4 – 1 = 3cm
=> OM = IJ = 3cm (Tính chất hình chữ nhật) (2)
Từ (1), (2) suy ra CD = AB (hai dây cách đều tâm thì bằng nhau). (đpcm)
ii. IO vuông góc với AC và BD
d) Chứng minh rằng: IA = IC; IB = ID; BC = AD. Tính T = \(IA^2+IB^2+IC^2+ID^2\)
Bài 12 (trang 106 SGK Toán 9 Tập 1)
Cho đường tròn tâm $O$ bán kính $5$cm, dây $AB$ bằng $8$cm.
a) Tính khoảng cách từ tâm $O$ đến dây $AB$.
b) Gọi $I$ là điểm thuộc dây $AB$ sao cho $AI = 1$cm. Kẻ dây $CD$ đi qua $I$ và vuông góc với $AB$. Chứng minh rằng $CD$ = $AB$.
Lời giải chi tiết
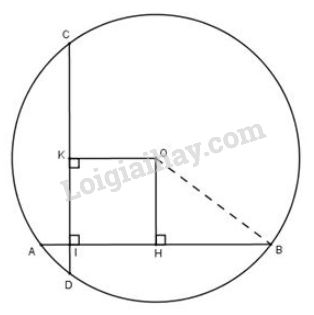
a) Kẻ OH⊥ABOH⊥AB tại H
Khi đó, đường tròn (O) có OH là 1 phần đường kính vuông góc với dây AB tại H
Suy ra HH là trung điểm của dây ABAB (Theo định lí 2 - trang 103)
⇒HA=HB=AB2=82=4cm.⇒HA=HB=AB2=82=4cm.
Xét tam giác HOBHOB vuông tại HH, theo định lí Pytago, ta có:
OB2=OH2+HB2⇔OH2=OB2−HB2OB2=OH2+HB2⇔OH2=OB2−HB2
⇔OH2=52−42=25−16=9⇒OH=3(cm)⇔OH2=52−42=25−16=9⇒OH=3(cm).
Vậy khoảng cách từ tâm OO đến dây ABAB là 3cm3cm.
b) Vẽ OK⊥CDOK⊥CD tại K
Tứ giác KOHIKOHI có ba góc vuông (ˆK=ˆH=ˆI=900)(K^=H^=I^=900) nên là hình chữ nhật, suy ra OK=HIOK=HI.
Ta có HI=AH−AI=4−1=3cmHI=AH−AI=4−1=3cm, suy ra OK=3cm.OK=3cm.
Vậy OH=OK=3cm.OH=OK=3cm.
Hai dây ABAB và CDCD cách đều tâm nên chúng bằng nhau.
Do đó AB=CD.
AB2=82=4cm." role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.2px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">
Xét tam giác vuông tại , theo định lí Pytago, ta có:
.
Vậy khoảng cách từ tâm đến dây là .
b) Vẽ tại K
Tứ giác có ba góc vuông nên là hình chữ nhật, suy ra .
Ta có
Bài 1: Cho đường tròn tâm O, bán kính 10cm và dây AB = 12cm. Tính khoảng cách từ tâm O đến dây AB
Lời giải:
Gọi dây trên là dây AB. Hạ OH⊥⊥AB = {H} (cd)
Xét (O) 1 phần đường kính OH: OH⊥⊥AB = {H} (cd)
=> H là trung điểm AB (đl) => HA = HB = AB: 2 = 12:2 = 6 (cm)
OH⊥⊥AB = {H} (cd) => ΔΔOHB vuông tại H (đn)
=> OH22+ HB22= OB22(Đl Py-ta-go)
T/s: OH22+ 622= R22
<=> OH22+36 = 1022=100
<=> OH22= 64 => OH = 8 (cm)
Gọi H là chân đường cao kẻ từ O
=> H là trung điểm AB
=> AH = AB/2 = 12/2 = 6 cm
Theo định lí Pytago cho tam giác AOH vuông tại H
\(AO^2=OH^2+AH^2\Rightarrow OH^2=AO^2-AH^2=100-36=64\Rightarrow OH=8\)cm
Cho đường tròn tâm O bán kính 5cm, dây AB bằng 8cm.
Tính khoảng cách từ tâm O đến dây AB.
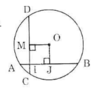
a) Kẻ OJ vuông góc với AB tại J.
Theo quan hệ vuông góc giữa đường kính và dây suy ra: J là trung điểm của AB.
![]()
Áp dụng định lí Pitago trong tam giác vuông OAJ có:
OJ2 = OA2 – AJ2 = 52 – 42 = 9 (OA = R = 5cm)
=> OJ = 3cm (1)
Vậy khoảng cách từ tâm O đến dây AB là OJ = 3cm.
Cho đường tròn tâm o bán kính 5cm khoảng cách từ tâm o đến dây AB=4cm. Tính độ dài dây AB
 ∆OBH vuông tại H
∆OBH vuông tại H
⇒ OB² = OH² + BH² (Pytago)
⇒ BH² = OB² - OH²
= 5² - 4²
= 9
⇒ BH = 3 (cm)
Do OH ⊥ AB
⇒ H là trung điểm của AB
⇒ AB = 2BH = 2.3 = 6 (cm)
Gọi OH là khoảng cách từ tâm O đến dây AB
=>OH\(\perp\)AB tại H
=>OH=4cm
ΔOAB cân tại O
mà OH là đường cao
nên H là trung điểm của AB
ΔOHA vuông tại H
=>\(OH^2+HA^2=OA^2\)
=>\(HA^2+4^2=5^2\)
=>\(HA^2=5^2-4^2=9\)
=>HA=3(cm)
H là trung điểm của AB
=>\(AB=2\cdot AH=6\left(cm\right)\)