Bài 3: Liên hệ giữa dây và khoảng cách từ tâm tới dây

Ta có: \(AB\perp CD\Rightarrow\) H là trung điểm CD (t/c bán kính vuông góc dây cung)

\(\Rightarrow\Delta ACD\) cân tại A (AH đồng thời là trung tuyến và đường cao)

\(\Rightarrow\widehat{ACD}=\widehat{ADC}\)

Mà \(\widehat{ADC}=\widehat{MCA}\) (cùng chắn AC)

\(\Rightarrow\widehat{ACD}=\widehat{MCA}\Rightarrow CA\) là phân giác của \(\widehat{MCD}\)

Áp dụng định lý phân giác trong tam giác MCH:

\(\dfrac{AM}{AH}=\dfrac{CM}{CH}\) (1)

Lại có \(\widehat{ACB}\) là góc nt chắn nửa đường tròn \(\Rightarrow\widehat{ACB}=90^0\)

\(\Rightarrow CB\perp CA\)

\(\Rightarrow CB\) là đường phân giác ngoài góc \(\widehat{MCD}\) của tam giác MCH

Áp dụng định lý phân giác: \(\dfrac{BM}{BH}=\dfrac{CM}{CH}\) (2)

(1);(2) \(\Rightarrow\dfrac{AM}{AH}=\dfrac{BM}{BH}\Rightarrow BM.AH=BH.AM\)

a: ΔOAB cân tại O

mà OI là trung tuyến

nên OI vuông góc AB

c: Xét ΔOAB có \(cosAOB=\dfrac{OA^2+OB^2-AB^2}{2\cdot OA\cdot OB}=\dfrac{R^2+R^2-3R^2}{2\cdot R\cdot R}=\dfrac{-1}{2}\)

=>góc AOB=120 độ

a: góc A+góc C=180 độ

=>ABCD nội tiếp đường tròn đường kính BD

b:

Gọi O là trung điểm của BD

=>ABCD nội tiếp đường tròn (O)

Vì BD là đường kính của đường tròn ngoại tiếp tứ giác ABCD

nên BD>AC

c: AC=BD

=>AC là đường kính của (O)

Xét tứ giác ABCD có

AC cắt BD tại trung điểm của mỗi đường

AC=BD

=>ABCD là hình chữ nhật

BC^2=AB^2+AC^2

=>ΔABC vuông tại A

=>AC là tiếp tuyến của (A;AB)

a: O cách đều ba cạnh thì O là tâm đường tròn nội tiếp

=>AO là phân giác của góc BAC: CO là phân giác của góc ACB

mà AO vuông góc BC: CO vuông góc AB

nên ΔABC đều

b: O cách đều hai cạnh thì AO là phân giác của góc BAC
mà AO vuông góc BC

nên ΔABC cân tại A

a: ΔOAB cân tại O

mà OM là trung tuyến

nên OM vuông góc AB và OM là trung trực của AB

\(OA=R=\sqrt{5^2+3^2}=\sqrt{34}\left(cm\right)\)

b: OM là trung trực của AB

=>C nằm trên trung trực của AB

=>CA=CB

=>ΔACB cân tại C

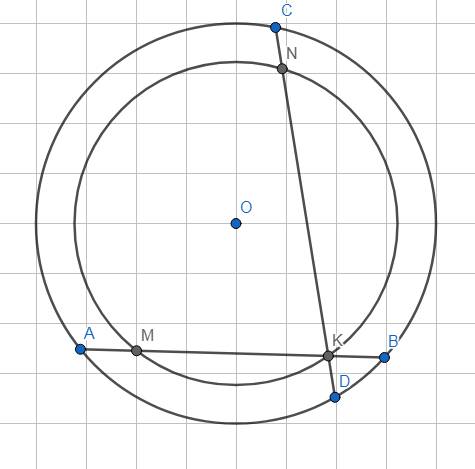
*TH₁: K nằm trong đường tròn \(\left(O\right)\).

- Xét \(\left(O\right)\),theo liên hệ giữa dây từ tâm tới dây, ta có:

\(AB< CD\Rightarrow h_{AB}>h_{CD}\) hay \(h_{MK}>h_{NK}\)

- Xét \(\left(O;OK\right)\), \(h_{MK}>h_{NK}\) nên \(MK< NK\left(đpcm\right)\)

- TH₂: K nằm ngoài đường tròn \(\left(O\right)\)\(\rightarrow CMTT\)