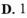Cho hình lập phương A B C D . A ' B ' C ' D ' . Mặt phẳng B D C ' chia khối lập phương thành hai phần. Tính tỉ lệ thể tích phần nhỏ so với phần lớn
A. 5 6
B. 1 5
C. 1 3
D. 1 6
Cho hình lập phương ABCD.A′B′C′D′ cạnh a. Khoảng cách từ điểm A đến mặt phẳng (A′B′CD) bằng
A. a 2
B. 3 a
C. 3 3 a
D. 2 2 a
Gọi O là tâm của hình vuông
A D D ' A ' ⇒ A O ⊥ A ' B ' C D ⇒ d A , A ' B ' C D = A O = 2 a 2
Chọn đáp án D.
Cho hình lập phương ABCD.A′B′C′D′ABCD.A′B′C′D′ cạnh aa và một điểm MM trên cạnh AB,AM=x,0<x<aAB,AM=x,0<x<a. Xét mặt phẳng (PP) đi qua điểm MM và chưa đường chéo A′C′A′C′ của hình vuông A′B′C′D′.A′B′C′D′.
1.1. Tính diện tích của thiết diện của hình lập phương cắt bởi mặt phẳng (PP).
2.2. Mặt phẳng (PP) chia hình lập phương thành hai khối đã diện. Hãy tìm xx để thể tích của một trong hai khối đa diện đó gấp đôi thể tích của khối đa diện kia.
Cho hình lập phương ABCD.A'B'C'D'. Tính tan của góc giữa hai mặt phẳng (A'BC) và (A'B'C'D')?
Cho hình lập phương ABCD.A′B′C′D′. Gọi O là tâm của hình vuông ABCD. Côsin của góc giữa hai mặt phẳng (OA′B′) và (OC′D′) bằng
![]()
![]()
![]()
![]()
Cho hình lập phương ABCD.A′B′C′D′. Gọi O là tâm của hình vuông ABCD. Côsin của góc giữa hai mặt phẳng (OA′B′) và (OC′D′) bằng
A. 2 5
B. 4 9
C. 8 25
D. 3 5
Gọi M, N lần lượt là trung điểm các cạnh A′B′,C′D′ ta có ((OA′B′), (OC′D′)) = (OM,ON).
Ta có
MN=a, 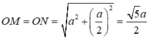
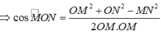
= 3 5
Chọn đáp án D.
Cho hình lập phương abcd.a'b'c'd' với A(0.0.0) B(1.0.0) D(0.1.0) A'(0.0.1). Biết rằng có hai mặt phẳng chứa A'C và tạo với mặt phẳng Oxy một góc a mà cosa = 1/(căn6). Góc giữa hai mặt phẳng đó là
Gọi mặt phẳng (P) chứa A'C có pt \(ax+by+cz+d=0\)
Do \(A'\left(0;0;1\right);C\left(1;1;0\right)\) \(\Rightarrow\left\{{}\begin{matrix}c+d=0\\a+b+d=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}c=-d\\b=-a-d\end{matrix}\right.\) (1)
\(\left\{{}\begin{matrix}\overrightarrow{n_{\left(P\right)}}=\left(a;b;c\right)\\\overrightarrow{n_{Oxy}}=\left(0;0;1\right)\end{matrix}\right.\) \(\Rightarrow cos\alpha=\frac{\left|c\right|}{\sqrt{a^2+b^2+c^2}}=\frac{1}{\sqrt{6}}\)
\(\Leftrightarrow6c^2=a^2+b^2+c^2\Leftrightarrow5c^2-a^2-b^2=0\) (2)
Thế (1) vào (2):
\(5d^2-a^2-\left(a+d\right)^2=0\Leftrightarrow2d^2-ad-a^2=0\)
\(\Leftrightarrow\left(2d+a\right)\left(d-a\right)=0\Rightarrow\left[{}\begin{matrix}a=d\Rightarrow b=-2d\\a=-2d\Rightarrow b=d\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\left(a;b;c\right)=\left(d;-2d;-d\right)=d\left(1;-2;-1\right)\\\left(a;b;c\right)=\left(-2d;d;-d\right)=-d\left(2;-1;1\right)\end{matrix}\right.\)
\(\Rightarrow\)Vecto pháp tuyến của hai mặt phẳng lần lượt là \(\left\{{}\begin{matrix}\overrightarrow{n_1}=\left(1;-2;-1\right)\\\overrightarrow{n_2}=\left(2;-1;1\right)\end{matrix}\right.\)
\(\Rightarrow\) Góc giữa 2 mặt phẳng:
\(cos\beta=\frac{\left|\overrightarrow{n_1}.\overrightarrow{n_2}\right|}{\left|\overrightarrow{n_1}\right|.\left|\overrightarrow{n_2}\right|}=\frac{\left|2+2-1\right|}{\sqrt{1+4+1}.\sqrt{4+1+1}}=\frac{1}{2}\) \(\Rightarrow\beta=60^0\)
Cho hình lập phương ABCD.A'B'C'D'. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, B'C', DD'. Hãy xác định thiết diện tạo bởi hình lập phương đã cho và mặt phẳng (MNP).
Cho hình lập phương ABCD.A'B'C'D' . Gọi R, N, Q là các điểm thuộc các cạnh A'D', BC, C'D'
a) Tìm giao điểm I và K của đường thẳng RQ với các mặt phẳng (AA'B'B), (BB'C'C)
b) Tìm giao điểm P và J của đường thẳng NK với các mặt phẳng (CC'D'D), (AA'B'B)
c) Tìm giao điểm S và M của đường thẳng IJ với các mặt phặng (ADD'A'), (ABCD)
d) Tìm giao tuyến của mặt phẳng (NQR) với các mặt phẳng của hình lập phương
e) Tìm thiết diện của mặt phẳng (NQR) với hình lập phương
Cho hình lập phương abcd.a'b'c'd' có cạnh bằng 2a tính góc giữa CC' và mặt phẳng AB'C'
Ta có ( CC' , (AB'C)) = ( CC' ,( ADC'B') (1) Có CO vuông góc C'D suy ra CO vg góc ( ADC'B' ) Suy ra (1) = góc CC'O = góc CC'D = 45 độ
Cho hình lập phương ABCDA'B'C'D'. Có bao nhiêu mặt trụ tròn xoay đi qua sáu đỉnh A, B, D, C', B', D'?
![]()
![]()