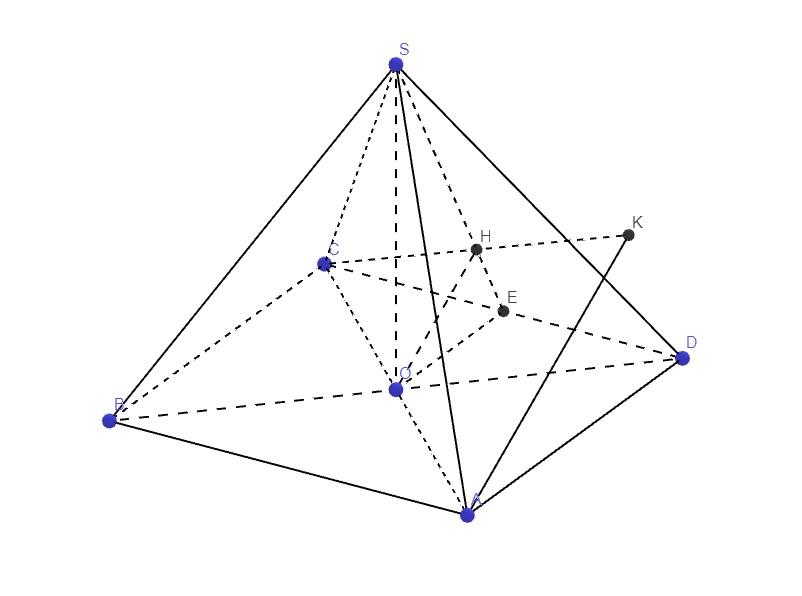
Cho hình chóp S.ABCD có đáy là hình bình hành. Các tam giác SAC và SBD là tam giác đều cạnh a. Gọi I, J lần lượt là trung điểm của SA, SB. Một mặt phẳng (a) di động qua IJ sao cho (a) cắt các cạnh SC, SD lần lượt tại M và N. Gọi P là giao điểm của IM và JN. Tìm giá trị nhỏ nhất của độ dài đoạn thẳng CP
Chương 2: ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG
Cho hình hộp ABCD.A'B'C'D'. Gọi M, N, P lần lượt là trung điểm của AB,B'C',DD'. Thiết diện của hình hộp đã cho cắt bởi mặt phẳng (MNP) là hình gì?
Chọn khẳng định đúng
A. Nếu a vuông góc với (P), b vuông góc với (P) thì a//b
B. Nếu a vuông góc (P), b//a thì b vuông góc với (P)
C. Nếu a vuông góc (P), (P) vuông góc với (Q) thì a vuông góc với (Q)
D. Nếu b vuông góc với (R), b vuông góc (P) thì (P)//(R)
a. Có thể a trùng b
b. Đúng
c. Có vô vàn trường hợp ko đúng, dễ thấy nhất là a thuộc (Q)
d. (P) và (R) có thể trùng nhau nữa
Đúng 2
Bình luận (3)
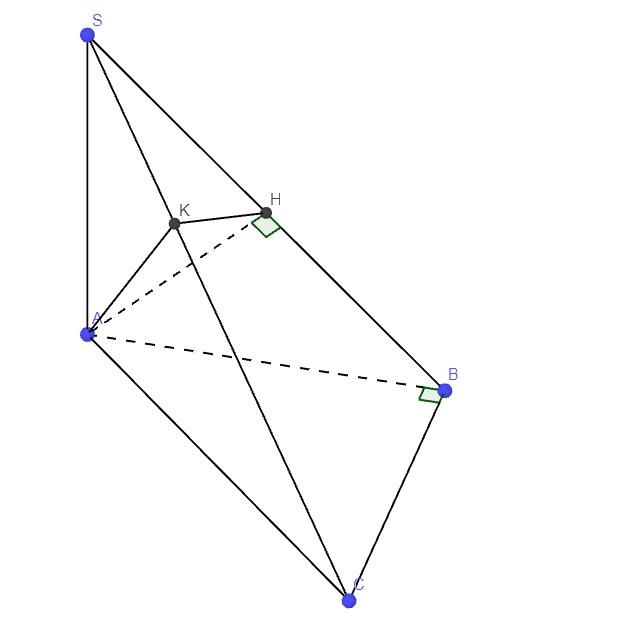
Cho hình chóp S.ABCD có đáy là hình chữ nhật,SA vuông góc với đáy, AD=2AB. Gọi H, K thứ tự là hình chiếu của A trên SB. CMR: SC vuông góc HK
Ủa bài này có vấn đề gì em nhỉ? Khá cơ bản (nhưng thiếu 1 đoạn K là hình chiếu lên đâu, chắc là SD).
Đúng 2
Bình luận (0)
Cho hình chóp S.ABCD có ABCD là nửa lục giác đều AB = BC = CD = 1/2AD.
a) CMR các mặt bên của hình chóp là các tam giác vuông
b) Gọi I, J thứ tự là hình chiếu của A trên SB, SC, SD. CMR: A,H,I,J đồng phẳng
Đề bài thiếu dữ liệu liên quan đỉnh S
Đúng 2
Bình luận (4)
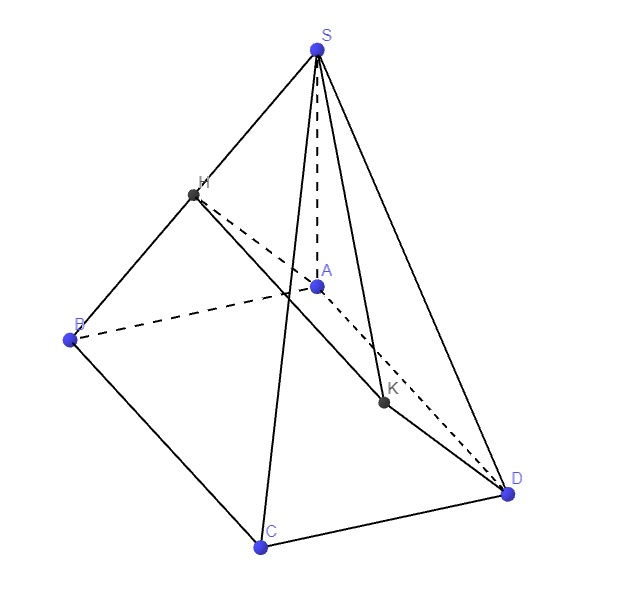
Cho hình chóp S.ABCD có đáy là hình vuông cạnh đáy bằng 2a, các cạnh bên đều bằng \(a\sqrt{5}\). Góc giữa SA và mặt phẳng (SCD)
Gọi E là trung điểm CD \(\Rightarrow CD\perp\left(SOE\right)\)
Kẻ \(OH\perp SE\Rightarrow OH\perp\left(SCD\right)\)
Qua A kẻ đường thẳng song song OH, cắt CH kéo dài tại K
\(\Rightarrow AK\perp\left(SCD\right)\Rightarrow\widehat{ASK}\) là góc giữa SA và (SCD)
\(SO=\sqrt{SA^2-OA^2}=a\sqrt{3}\)
\(OH=\dfrac{SO.OE}{\sqrt{SO^2+OE^2}}=\dfrac{a\sqrt{3}}{2}\)
\(AK=2OH=a\sqrt{3}\) (đường trung bình)
\(sin\widehat{ASK}=\dfrac{AK}{SA}=\dfrac{\sqrt{15}}{5}\)
Đúng 1
Bình luận (1)
Cho lăng trụ đều ABC.A'B'C' có AB =1, AA' = \(\sqrt{2}\) . Tính góc giữa AB' và BC'
\(AB'=BC'=\sqrt{1+2}=\sqrt{3}\)
\(\overrightarrow{AB'}.\overrightarrow{BC'}=\left(\overrightarrow{AA'}+\overrightarrow{AB}\right)\left(\overrightarrow{BC}+\overrightarrow{BB'}\right)=AA'^2+\overrightarrow{AB}.\overrightarrow{BC}=2+1.1.cos120^0=\dfrac{3}{2}\)
\(\Rightarrow cos\left(AB';BC'\right)=\dfrac{\left|\overrightarrow{AB'}.\overrightarrow{BC'}\right|}{AB'.BC'}=\dfrac{1}{2}\)
Đúng 3
Bình luận (4)
Cho hình chóp S.ABC có đấy là tam giác ABC Vuông cân tại B , SA vuông mặt đáy . Gọi H là hình chiếu của A lên SB a, CM AH vuông mặt phẳng SBC b, tính góc giữa 2 mặt phẳng (SAC)& (SBC). Biết SA=AB=a
a.
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow BC\perp AH\)
Mà \(AH\perp SB\left(gt\right)\)
\(\Rightarrow AH\perp\left(SBC\right)\)
b.
Từ H kẻ \(HK\perp SC\) (K thuộc SC) (1)
Do \(AH\perp\left(SBC\right)\Rightarrow AH\perp SC\) (2)
\(\left(1\right);\left(2\right)\Rightarrow SC\perp\left(AHK\right)\)
Mà \(SC=\left(SAC\right)\cap\left(SBC\right)\)
\(\Rightarrow\widehat{AKH}\) là góc giữa (SAC) và (SBC)
\(SC\perp\left(AHK\right)\Rightarrow SC\perp AK\)
\(AC=AB\sqrt{2}=a\sqrt{2}\)
Áp dụng hệ thức lượng trong tam giác vuông SAC:
\(AK=\dfrac{SA.AC}{\sqrt{SA^2+AC^2}}=\dfrac{a\sqrt{6}}{3}\)
Hệ thức lượng trong tam giác vuông SAB:
\(AH=\dfrac{SA.AB}{\sqrt{SA^2+AB^2}}=\dfrac{a\sqrt{2}}{2}\)
\(AH\perp\left(SBC\right)\Rightarrow AH\perp HK\Rightarrow\Delta AHK\) vuông tại H
\(sin\widehat{AKH}=\dfrac{AH}{AK}=\dfrac{\sqrt{3}}{2}\Rightarrow\widehat{AKH}=60^0\)
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB=a, AD=acăn3. Cạnh bên SA vuông góc với mặt phẳng đáy và SA=a. Gọi alpha là góc giữa đường thẳng SD và mặt phẳng (SBC). Tanalpha=?
Từ A kẻ \(AH\perp SB\) (H thuộc SB)
Qua H kẻ đường thẳng d song song BC. Qua D kẻ đường thẳng song song AH cắt d tại K
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow BC\perp AH\)
\(\Rightarrow AH\perp\left(SBC\right)\)
Mà \(DK||AH\Rightarrow DK\perp\left(SBC\right)\)
\(\Rightarrow\widehat{DSK}\) là góc giữa SD và (SBC)
\(SD=\sqrt{SA^2+AD^2}=2a\)
\(DK=AH=\dfrac{SA.AB}{\sqrt{SA^2+AB^2}}=\dfrac{a\sqrt{2}}{2}\)
\(SK=\sqrt{SD^2-DK^2}=\dfrac{a\sqrt{14}}{2}\)
\(\Rightarrow tan\widehat{DSK}=\dfrac{DK}{SK}=\dfrac{\sqrt{7}}{7}\)
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có AB=CD=a. Gọi M, N lần lượt là trung điểm của AD và BC. Biết MN=căn3a, góc giữa hai đường thẳng AB và CD bằng?
Đề bài của em bị sai, \(AB=CD=2a\) mới đúng, vì nếu \(AB=CD=a\) thì \(MN=a\sqrt{3}\) không thể tồn tại do nó vi phạm bất đẳng thức tam giác
Đúng 0
Bình luận (0)