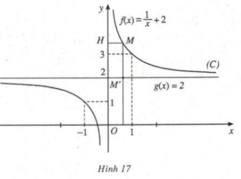
Tính l i m n → 0 1 x + 2 và nêu nhận xét về khoảng cách MH khi x → 0 (H.17)
PB
Những câu hỏi liên quan
1) Viết mỗi tập hợp sau bằng cách liệt kê các phần tử
a) A { x thuộc N / x m x ( m +1 ) với m 0 ; 1 ; 2 ; 3 ; 4
b) B { x thuộc N / 2 x m với m 0 ; 1 ; 2 ; 3 ; 4 ; 5
c) C { x thuộc N / x 3 x a - 2 với a 0 ; 1 ; 3 ; 5 ; 7
d) D { x thuộc N / x m x n x n với n 0 ; 1 ; 2 ; 3 ; 4
giúp mink với mink đang cần gấp lắm luôn
ai làm nhanh mà đúng mink tick cho
Đọc tiếp
1) Viết mỗi tập hợp sau bằng cách liệt kê các phần tử
a) A = { x thuộc N / x = m x ( m +1 ) với m = 0 ; 1 ; 2 ; 3 ; 4
b) B = { x thuộc N / 2 x m với m = 0 ; 1 ; 2 ; 3 ; 4 ; 5
c) C = { x thuộc N / x = 3 x a - 2 với a = 0 ; 1 ; 3 ; 5 ; 7
d) D = { x thuộc N / x = m x n x n với n = 0 ; 1 ; 2 ; 3 ; 4
giúp mink với mink đang cần gấp lắm luôn
ai làm nhanh mà đúng mink tick cho
khó quá
xin lỗi nhé mik ko làm đc
Đúng 0
Bình luận (1)
Xem thêm câu trả lời
Dạng 1. Tìm giá trị của x để biểu thức nhận giá trị nguyên
Bài 1. Cho A frac{2}{sqrt{x}-1} với x ≥ 0, x ≠ 1. Tìm x nguyên để A nhận giá trị là số nguyên
Bài 2. Cho B frac{sqrt{x}-5}{sqrt{x}+3} với x ≥ 0. Tìm x nguyên để B nhận giá trị là số nguyên
Bài 3. Cho C frac{sqrt{x}-1}{sqrt{x}+2} với x ≥ 0. Tìm x nguyên để C nhận giá trị là số nguyên dương
Bài 4. Cho D frac{3sqrt{x}}{sqrt{x}-3} với x 0,x ≠ 1. Tìm x ∈ N để D có giá trị là số nguyên
Bài 5. Cho D frac{5}{sqrt{x}+1} với x ≥ 0. Tìm...
Đọc tiếp
Dạng 1. Tìm giá trị của x để biểu thức nhận giá trị nguyên
Bài 1. Cho A = \(\frac{2}{\sqrt{x}-1}\) với x ≥ 0, x ≠ 1. Tìm x nguyên để A nhận giá trị là số nguyên
Bài 2. Cho B = \(\frac{\sqrt{x}-5}{\sqrt{x}+3}\) với x ≥ 0. Tìm x nguyên để B nhận giá trị là số nguyên
Bài 3. Cho C = \(\frac{\sqrt{x}-1}{\sqrt{x}+2}\) với x ≥ 0. Tìm x nguyên để C nhận giá trị là số nguyên dương
Bài 4. Cho D = \(\frac{3\sqrt{x}}{\sqrt{x}-3}\) với x > 0,x ≠ 1. Tìm x ∈ N để D có giá trị là số nguyên
Bài 5. Cho D = \(\frac{5}{\sqrt{x}+1}\) với x ≥ 0. Tìm x để D nhận giá trị là số nguyên
Bài 6. Cho E = \(\frac{4\sqrt{x}+1}{\sqrt{x}+1}\) với x ≥ 0. Tìm x ∈ R để E nhận giá trị là số nguyên
1. Tìm x sao cho :(x-7).(x-3) < 0
Cho S = 1 - 3 + 3^2 - 3^3 + .......+3^98 - 3^99
a) Chứng minh rằng S là bội của -20
b) Tính S , từ đó suy ra 3^100 chia cho 4 dư 1
2.Tìm số nguyên dương n sao cho n + 2 là ước của 111 còn n - 2 là bội của 11
3.Tìm n thuộc Z sao cho n - 1 là bội của n +5 và n + 5 là bội của n -1
Bài 1:Quy đồng mẫu thức thành các phân thức sau:
5/x^5y^3 và 7/12x^3y^4
Bài 2:Giải các phương trình sau:
a)(x-1)(3x+1)0
b)(x-1)(x+2)(x-3)0
c)(5x+3)(x^2+4)(x-4)0
d)(3,1x-6,2)(0,5x+1)0
e)(2x+1)(x+4)(3x-2)0
f)(7x-2)(2x-1)(x+3)0
g)(4x-1)(x-3)-(x-3)(5x+2)0
h)(x+3)(x-5)+(x+3)(3x-4)0
i)(x+6)(3x+1)+x^2-360
j)(x+4)(5x+9)-x^2+160
Không biết giờ này mọi người còn thức không nhưng mà mọi người nhớ làm ráng những bài tập này giúp em!!Em xin chân thành cảm ơn những người sẽ làm giúp em những bài...
Đọc tiếp
Bài 1:Quy đồng mẫu thức thành các phân thức sau:
5/x^5y^3 và 7/12x^3y^4
Bài 2:Giải các phương trình sau:
a)(x-1)(3x+1)=0
b)(x-1)(x+2)(x-3)=0
c)(5x+3)(x^2+4)(x-4)=0
d)(3,1x-6,2)(0,5x+1)=0
e)(2x+1)(x+4)(3x-2)=0
f)(7x-2)(2x-1)(x+3)=0
g)(4x-1)(x-3)-(x-3)(5x+2)=0
h)(x+3)(x-5)+(x+3)(3x-4)=0
i)(x+6)(3x+1)+x^2-36=0
j)(x+4)(5x+9)-x^2+16=0
Không biết giờ này mọi người còn thức không nhưng mà mọi người nhớ làm ráng những bài tập này giúp em!!Em xin chân thành cảm ơn những người sẽ làm giúp em những bài tập trên ạ!
Bài phân thức thì bởi vì ko có dấu gạch ngang nên em dùng dấu / thay cho dấu gạch ngang.
mọi người ráng làm giúp em nha!!!
Bài 1:
\(\frac{5}{x^5y^3}=\frac{5y.12}{12x^5y^4}=\frac{60y}{12x^5y^4}\)
\(\frac{7}{12x^3y^4}=\frac{7.5x^2}{12.5x^5y^4}=\frac{35x^2}{60x^5y^4}\)
Bài 2:
a)
$(x-1)(3x+1)=0$
\(\Rightarrow \left[\begin{matrix} x-1=0\\ 3x+1=0\end{matrix}\right.\Rightarrow \left[\begin{matrix} x=1\\ x=-\frac{1}{3}\end{matrix}\right.\)
b)
$(x-1)(x+2)(x-3)=0$
\(\Rightarrow \left[\begin{matrix} x-1=0\\ x+2=0\\ x-3=0\end{matrix}\right.\Rightarrow \left[\begin{matrix} x=1\\ x=-2\\ x=3\end{matrix}\right.\)
c)
$(5x+3)(x^2+4)(x-4)=0$
\(\Rightarrow \left[\begin{matrix} 5x+3=0\\ x^2+4=0\\ x-4=0\end{matrix}\right.\Rightarrow \left[\begin{matrix} x=-\frac{3}{5}\\ x^2=-4< 0(\text{vô lý})\\ x=4\end{matrix}\right.\)
Vậy $x=-\frac{3}{5}$ hoặc $x=4$
d)
\((3,1x-6,2)(0,5x+1)=0\)
\(\Rightarrow \left[\begin{matrix} 3,1x-6,2=0\\ 0,5x+1=0\end{matrix}\right.\Rightarrow \left[\begin{matrix} x=2\\ x=-2\end{matrix}\right.\)
e)
\((2x+1)(x+4)(3x-2)=0\)
\(\Rightarrow \left[\begin{matrix} 2x+1=0\\ x+4=0\\ 3x-2=0\end{matrix}\right.\Rightarrow \left[\begin{matrix} x=\frac{-1}{2}\\ x=-4\\ x=\frac{2}{3}\end{matrix}\right.\)
f)
\((7x-2)(2x-1)(x+3)=0\)
\(\Rightarrow \left[\begin{matrix} 7x-2=0\\ 2x-1=0\\ x+3=0\end{matrix}\right.\Rightarrow \left[\begin{matrix} x=\frac{2}{7}\\ x=\frac{1}{2}\\ x=-3\end{matrix}\right.\)
g)
\((4x-1)(x-3)-(x-3)(5x+2)=0\)
\(\Leftrightarrow (x-3)[(4x-1)-(5x+2)]=0\)
\(\Leftrightarrow (x-3)(-x-3)=0\Rightarrow \left[\begin{matrix} x-3=0\\ -x-3=0\end{matrix}\right.\Rightarrow \left[\begin{matrix} x=3\\ x=-3\end{matrix}\right.\)
h)
\((x+3)(x-5)+(x+3)(3x-4)=0\)
$\Leftrightarrow (x+3)(x-5+3x-4)=0$
$\Leftrightarrow (x+3)(4x-9)=0$
\(\Rightarrow \left[\begin{matrix} x+3=0\\ 4x-9=0\end{matrix}\right.\Rightarrow \left[\begin{matrix} x=-3\\ x=\frac{9}{4}\end{matrix}\right.\)
i)
\((x+6)(3x+1)+x^2-36=0\)
$\Leftrightarrow (x+6)(3x+1)+(x-6)(x+6)=0$
$\Leftrightarrow (x+6)(3x+1+x-6)=0$
$\Leftrightarrow (x+6)(4x-5)=0$
\(\Rightarrow \left[\begin{matrix} x+6=0\\ 4x-5=0\end{matrix}\right.\Rightarrow \left[\begin{matrix} x=-6\\ x=\frac{5}{4}\end{matrix}\right.\)
j)
$(x+4)(5x+9)-x^2+16=0$
$\Leftrightarrow (x+4)(5x+9)-(x^2-16)=0$
$\Leftrightarrow (x+4)(5x+9)-(x-4)(x+4)=0$
$\Leftrightarrow (x+4)(5x+9-x+4)=0$
$\Leftrightarrow (x+4)(4x+13)=0$
\(\Rightarrow \left[\begin{matrix} x+4=0\\ 4x+13=0\end{matrix}\right.\Rightarrow \left[\begin{matrix} x=-4\\ x=-\frac{13}{4}\end{matrix}\right.\)
Khi gõ đề bài bạn ấn vào biểu tượng $\sum$ để gõ công thức toán nhé.
Bài 5:
a) Cho x0, y0 và m, n là hai số thực. Chứng minh rằngfrac{m^2}{x}+frac{n^2}{y}≥frac{left(m+nright)^2}{x+y}
b) Cho a, b, c là ba số dương thỏa mãn abc1.
Chứng minh rằng frac{1}{a^3left(b+cright)}+frac{1}{b^3left(c+aright)}+frac{1}{c^3left(a+bright)}≥frac{3}{2}
Đọc tiếp
Bài 5:
a) Cho x>0, y>0 và m, n là hai số thực. Chứng minh rằng\(\frac{m^2}{x}+\frac{n^2}{y}\)≥\(\frac{\left(m+n\right)^2}{x+y}\)
b) Cho a, b, c là ba số dương thỏa mãn abc=1.
Chứng minh rằng \(\frac{1}{a^3\left(b+c\right)}+\frac{1}{b^3\left(c+a\right)}+\frac{1}{c^3\left(a+b\right)}\)≥\(\frac{3}{2}\)
b) với mọi a,b,c ϵ R và x,y,z ≥ 0 có :
\(\frac{a^2}{x}+\frac{b^2}{y}+\frac{c^2}{z}\ge\frac{\left(a+b+c\right)^2}{x+y+z}\left(1\right)\)
Dấu ''='' xảy ra ⇔\(\frac{a}{x}=\frac{b}{y}=\frac{c}{z}\)
Thật vậy với a,b∈ R và x,y ≥ 0 ta có:
\(\frac{a^2}{x}=\frac{b^2}{y}\ge\frac{\left(a+b\right)^2}{x+y}\left(2\right)\)
⇔\(\frac{a^2y}{xy}+\frac{b^2x}{xy}\ge\frac{\left(a+b\right)^2}{x+y}\)
⇔\(\frac{a^2y+b^2x}{xy}\ge\frac{\left(a+b\right)^2}{x+y}\)
⇔\(\frac{a^2y+b^2x}{xy}.\left(x+y\right)xy\ge\frac{\left(a+b\right)^2}{x+y}.\left(x+y\right)xy\)
⇔\(\left(a^2y+b^2x\right)\left(x+y\right)\ge\left(a+b\right)^2xy\)
⇔\(a^2xy+b^2x^2+a^2y^2+b^2xy\ge a^2xy+2abxy+b^2xy\)
⇔\(b^2x^2+a^2y^2-2abxy\ge0\)
⇔\(\left(bx-ay\right)^2\ge0\)(luôn đúng )
Áp dụng BĐT (2) có:
\(\frac{a^2}{x}+\frac{b^2}{y}+\frac{c^2}{z}\ge\frac{\left(a+b\right)^2}{x+y}+\frac{c^2}{z}=\frac{\left(a+b+c\right)^2}{x+y+z}\)
Dấu ''='' xảy ra ⇔\(\frac{a}{x}=\frac{b}{y}=\frac{c}{z}\)
Ta có:
\(\frac{1}{a^3\left(b+c\right)}+\frac{1}{b^3\left(c+a\right)}+\frac{1}{c^3\left(a+b\right)}
\)
= \(\frac{1}{a^2}.\frac{1}{ab+ac}+\frac{1}{b^2}.\frac{1}{bc+ac}+\frac{1}{c^2}.\frac{1}{ac+bc}\)
=\(\frac{\frac{1}{a^2}}{ab+ac}+\frac{\frac{1}{b^2}}{bc+ab}+\frac{\frac{1}{c^2}}{ac+bc}\)
Áp dụng BĐT (1) ta có:
\(\frac{\frac{1}{a^2}}{ab+ac}+\frac{\frac{1}{b^2}}{bc+ab}+\frac{\frac{1}{c^2}}{ac+bc}\ge\frac{\left(\frac{1}{a}+\frac{1}{b}++\frac{1}{c}\right)^2}{2\left(ab+bc+ac\right)}\)
Mà abc=1⇒\(\left\{{}\begin{matrix}ab=\frac{1}{c}\\bc=\frac{1}{a}\\ac=\frac{1}{b}\end{matrix}\right.\)
\(\frac{\frac{1}{a^2}}{ab+ac}+\frac{\frac{1}{b^2}}{bc+ac}+\frac{\frac{1}{c^2}}{ac+bc}\ge\frac{\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)^2}{2\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)}\)
\(\frac{\frac{1}{a^2}}{ab+ac}+\frac{\frac{1}{b^2}}{bc+ac}+\frac{\frac{1}{c^2}}{ac+bc}\ge\frac{1}{2}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\)
Có \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge3\sqrt[3]{\frac{1}{abc}}=3\sqrt[3]{\frac{1}{1}}=3\)( BĐT cosi )
⇒\(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge3\)
⇒\(\frac{\frac{1}{a^2}}{ab+ac}+\frac{\frac{1}{b^2}}{bc+ac}+\frac{\frac{1}{c^2}}{ac+bc}\ge\frac{1}{2}.3=\frac{3}{2}\)
Vậy \(\frac{1}{a^3\left(b+c\right)}+\frac{1}{b^3\left(c+a\right)}+\frac{1}{c^3\left(a+b\right)}\ge\frac{3}{2}\)
Chúc bạn học tốt !!!
mọi người à, có thể làm giúp tớ mấy câu hỏi tìm x này không? cảm ơn rất nhiều ≥√≤
a, |x| + |x-1| = 0
b, |x| + |x-1| = 1
c, |x| + |x-1| = 1/2 d, |x| + |x-1| = 5 e, |x| + |x^3| = 0 f, |x-1| + |x^2 - 1| = 0 g, x^2 + |x| = 0 h, (x-1)^2 + |x^2 - 1| = 0 cảm ơn cậu một lần nữa nhé, vì đã giúp mình làm bài này <3
a, vì |x| ≥ 0 và |x-1| ≥ 0
dấu bằng xảy ra khi và chỉ khi |x|=0 và |x-1|=0
=> x=0 và x=1
Đúng 0
Bình luận (0)
Tìm số nguyên x thỏa mãn
a) ( x + 4 ) : ( x + 1 )
b) (4x + 3 ) : ( x - 2 )
Gợi ý phần a
Có x + 4 ( x + 1 ) + 3
nên ( x + 4 ) : ( x + 1 ) khi 3: ( x + 1 ) hay x + 1 là ước của 3
Các ước của 3 là: 1 , 3 , - 1 , - 3
x + 1 1 thì x 0
x + 1 3 thì x 2
x + 1 - 1 thì x - 2
x + 1 - 3 thì x - 4
Làm hộ mk phần b
Đọc tiếp
Tìm số nguyên x thỏa mãn
a) ( x + 4 ) : ( x + 1 )
b) (4x + 3 ) : ( x - 2 )
Gợi ý phần a
Có x + 4 = ( x + 1 ) + 3
nên ( x + 4 ) : ( x + 1 ) khi 3: ( x + 1 ) hay x + 1 là ước của 3
Các ước của 3 là: 1 , 3 , - 1 , - 3
x + 1 = 1 thì x = 0
x + 1 = 3 thì x = 2
x + 1 = - 1 thì x = - 2
x + 1 = - 3 thì x = - 4
Làm hộ mk phần b
b) Giải:
Ta có: \(4x+3⋮x-2\)
\(\Rightarrow4x-8+11⋮x-2\)
\(\Rightarrow4\left(x-2\right)+11⋮x-2\)
\(\Rightarrow11⋮x-2\)
\(\Rightarrow x-2\in\left\{1;-1;11;-11\right\}\)
\(\left[\begin{matrix}x-2=1\\x-2=-1\\x-2=11\\x-2=-11\end{matrix}\right.\Rightarrow\left[\begin{matrix}x=3\\x=1\\x=13\\x=-9\end{matrix}\right.\)
Vậy \(x\in\left\{3;1;13;-9\right\}\)
Đúng 0
Bình luận (0)
b.Ta có:(4x+3)=4x-4.2+8+3
=4(x-2)+11
Để(4x+3)chia hết cho (x-2)
#11chia hết cho (x-2)(#là khi và chỉ khi nhế!)
#x-2€ Ư(11)={±1;±11}
#x€{3;1;13;-9}
Vậy x€{3;1;13;-9}
Đúng 0
Bình luận (0)
Bài tập:Tìm m để phương trình
a)x2+2mx-m2+m-3=0 nhận x=2 là nghiệm.Tìm nghiệm còn lại
b)2x2-4x+3m-5=0 nhận x=-1 là nghiệm.Tìm nghiệm còn lại
c)x2+(m-2)x-m+1=0 nhận x=2018+\(\sqrt{2019}\)
làm nghiệm
d)x2-2(m-1)x+m2-2m-3=0 nhận x=2004-2\(\sqrt{113}\) làm nghiệm
a) thay x=2 vào PT (a) ta được:
\(4+4m-m^2+m-3=0\Leftrightarrow-m^2+5m+1=0\\ \)
\(\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{5+\sqrt{29}}{2}\\m=\dfrac{5-\sqrt{29}}{2}\end{matrix}\right.\)
gọi x=x1=2, x2 là nghiệm còn lại.
theo viet x1+x2 =-2m.
=> x2=-2m-2
* \(m=\dfrac{5+\sqrt{29}}{2}.\\\Rightarrow x2=-\sqrt{29}-5-2=-7-\sqrt{29}\)
*\(m=\dfrac{5-\sqrt{29}}{2}\\ \Rightarrow x2=\sqrt{29}-5-2=-7+\sqrt{29}\)
vậy ....
câu b) bạn có thể làm tương tự
Đúng 0
Bình luận (0)
c) ta có: a=1;
\(\Delta=\left(m-2\right)^2-4\left(1-m\right)=m^2\);
*\(x=\dfrac{-b+\sqrt{\Delta}}{2a}=2018+\sqrt{2019}\\ \Leftrightarrow-\left(m-2\right)+\left|m\right|=4036+2\sqrt{2019}\)
<=>\(\left[{}\begin{matrix}\left\{{}\begin{matrix}m>0\\-m+2+m=4036+2\sqrt{2019}\left(VN\right)\end{matrix}\right.\\\left\{{}\begin{matrix}m< 0\\-m+2-m=4036+2\sqrt{2019}\end{matrix}\right.\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}m< 0\\m=-2017-\sqrt{2019}\end{matrix}\right.\)<=>\(m=-2017-\sqrt{2019}\)
* \(x=\dfrac{-b-\sqrt{\Delta}}{2a}\) (xét tương tự => vô nghiệm).
vậy \(m=-2017-\sqrt{2019}\)
Đúng 0
Bình luận (0)
a=1
\(\Delta'=\left(m-1\right)^2-\left(m^2-2m-3\right)=4\)
*\(x=\dfrac{-b'+\sqrt{\Delta'}}{a}=2004-2\sqrt{113}\)
\(\Leftrightarrow m-1+2=2004-2\sqrt{113}\Leftrightarrow m=2003-2\sqrt{113}\)
*\(x=\dfrac{-b'-\sqrt{\Delta'}}{a}=2004-2\sqrt{113}\)
\(\Leftrightarrow m-1-2=2004-2\sqrt{113}\Leftrightarrow2007-2\sqrt{113}\)
Đúng 0
Bình luận (2)
Cho PT x2 - mx - 4 = 0 ( I ) ( m là tham số )
Tìm m để PT ( I ) có 2 nghiệm phân biệt x1, x2 thỏa mãn ( x1 + 1 )2 + ( x2 + 1 )2 = 10
https://i.imgur.com/alzfUzh.jpg
1) Tìm số nguyên x, biết: \(\dfrac{x}{4}\)=\(\dfrac{16}{x}\) và x< 0.
2) Tìm các giá trị là số nguyên.
\(\dfrac{x-3}{x-1}\) có giá trị là số nguyên.
3) Cho A= \(\dfrac{n+8}{2n+5}\) (n ∈ N* ). Tìm các giá trị của n để A là số nguyên tố.
Câu 1:
=>x^2=64
=>x=8(loại) hoặc x=-8(nhận)
Đúng 0
Bình luận (0)