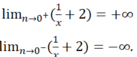
Khi x dần đến 0 thì độ dài đoạn MH cũng dần đến 0.
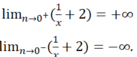
Khi x dần đến 0 thì độ dài đoạn MH cũng dần đến 0.
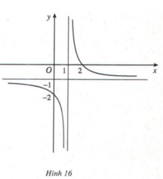
Cho hàm số y = (2 - x)/(x - 1) (H.16) có đồ thị (C).
Nêu nhận xét về khoảng cách từ điểm M(x; y) ∈ (C) tới đường thẳng y = -1 khi |x| → +∞
Cho mặt phẳng P : x + m z - m = 0 và mặt phẳng Q : ( 1 - m ) x - m y = 0 (tham số m # 0 ). Gọi d = P ∩ Q . Xét các mặt phẳng α chứa (d), xét điểm A 2 ; 1 ; 1 . Khi đó gọi h là khoảng cách từ A đến (d) thì GTLN của h h m a x bằng bao nhiêu?
![]()
![]()
![]()
![]()
Cho (P): x - y - z - 3 = 0, d : x - 2 = 4 3 = z 5 . Gọi A = d ∩ P và M là trung điểm OA. Tính khoảng cách h từ M tới (P):
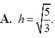
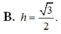
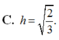
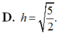
Trong không gian với hệ tọa độ Oxyz cho điểm A (2; 1; 3) và mặt phẳng (P): x + my + (2m + 1)z – m – 2 = 0, m là tham số. Gọi H (a; b; c) là hình chiếu vuông góc của điểm A trên (P). Tính a + b khi khoảng cách từ điểm A đến (P) lớn nhất?
A. a + b = -1/2
B. a + b = 2
C. a + b = 0
D. a + b = 3/2
Trong không gian với hệ tọa độ Oxyz cho điểm A(2;1;3) và mặt phẳng (P): x + my + (2m + 1) - m - 2 = 0. Gọi H (a;b;c) là hình chiếu vuông góc của điểm A trên (P) Khi khoảng cách từ điểm A đến (P) lớn nhất, tính a + b
A. 2
B. 1
C. 3 2
D. 0
Cho điểm M(1; 4; 2) và mặt phẳng (α): x + y + z – 1 = 0. Tính khoảng cách từ M đến mp(α).
Cho hai đường thẳng chéo nhau: d : x = 2 - t y = - 1 + t z = 1 - t d ' : x = 2 + 2 t y = t z = 1 + t
Lấy hai điểm M(2; -1; 1) và M'(2; 0; 1) lần lượt trên d và d'. Tính khoảng cách từ M đến mặt phẳng ( β) và khoảng cách từ M' đến mặt phẳng (α). So sánh hai khoảng cách đó.
Trong không gian với hệ tọa độ Oyz cho điểm A (2;1;3) và mặt phẳng (P): x+my+ (2m+1)z-m-2=0, m là tham số. Gọi H (a;b;c) là hình chiếu vuông góc của điểm A trên (P). Tính a+b khi khoảng cách từ điểm A đến (P) lớn nhất?
A. a + b = - 1 2
B. a+b=2
C. a+b=0
D. a + b = 3 2
Trong không gian với hệ tọa độ Oxyz, cho điểm A(2;1;3) và mặt phẳng P : x + m y + ( 2 m + 1 ) z - ( 2 + m ) = 0 với m là tham số. Gọi điểm H(a;b;c) là hình chiếu vuông góc của điểm A trên (P). Tính a+b khi khoảng cách từ điểm A đến (P) lớn nhất.
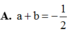
![]()
![]()
![]()