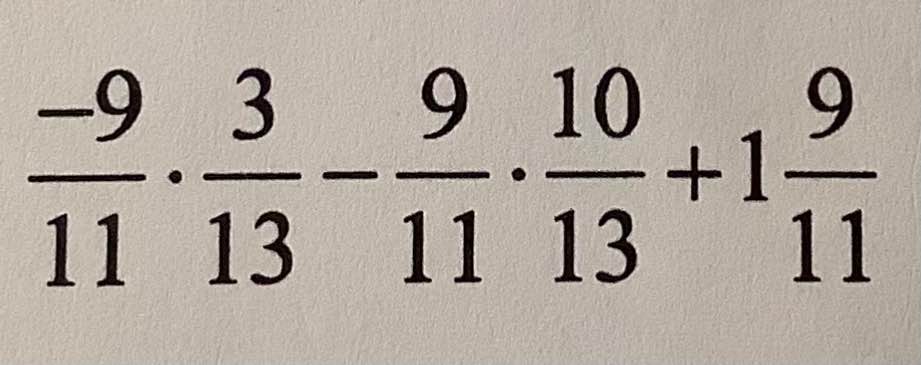Bài 3: Tính chất cơ bản của phân số

Ta có `:`

`A=(20n + 13)/(4n+3) = (20n + 15 -  2)/(4n+3) = (20n+15)/(4n+3) - 2/(4n+3) = (5(4n+3))/(4n+3) - 2/(4n+3) = 5 - 2/(4n+3)`

Để `A` đạt giá trị nhỏ nhất

`=>2/(4n+3)` phải là số dương lớn nhất

Để `2/(4n+3)` dương lớn nhất

`=>4n+3` nhỏ nhất mà `n in Z` 

Xét `4n+3=1`

`=>n cancelin Z`

Xét `4n+3=2`

`=>n cancelin Z`

Xét `4n+3=3`

`=>n =0(t//m)`

`=>A=5-2/3 = 13/3`

Vậy `GTN N` của `A=13/3` khi  `n=0`

\(\dfrac{-7}{x+1}=\dfrac{6}{x+27}\)

\(\Rightarrow-7x-189=6x+6\)

\(\Rightarrow-7x-6x=6+189\)

\(\Rightarrow-13x=195\)

\(\Rightarrow x=-15\)

Vay x = -15

\(\dfrac{-7}{x+1}=\dfrac{6}{x+27}\)

\(\Rightarrow-7\left(x+27\right)=6\left(x+1\right)\)

\(\Rightarrow-7x-189=6x+6\)

\(\Rightarrow-7x-6x=6+189\)

\(\Rightarrow-13x=195\)

\(\Rightarrow x=-15\)

Vậy x=-15

Nhận thấy 1/1.2.3 = 1/2.3;    1/1.2.3.4 < 1/3.4;   1/1.2.3.4.5 < 1/4.5;                               1/1.2.3...n  < 1/n(n-1)

=> 1 + 1/1.2 + 1/1.2.3 +... + 1/1.2.3...n < 1 + 1/1.2 + 1/2.3 + 1/3.4 + ... + 1/n(n-1)

=>  1 + 1/1.2 + 1/1.2.3 +... + 1/1.2.3...n < 1 + 1 -1/2 + 1/2 - 1/3 + 1/3 - 1/4 +...+            1/n-1 - 1/n

=>1 + 1/1.2 + 1/1.2.3 +... + 1/1.2.3...n < 2  - 1/n < 2

=> đpcm

Số phần của bể vòi nước chảy được trong 1 giờ:
\(1:5=\dfrac{1}{5}\left(bể\right)\)
Số phần trăm của bể nếu vòi nước chảy trong 3 giờ:
\(\dfrac{1}{5}\times3=\dfrac{3}{5}=0,6=60\%\)

Mỗi giờ vòi nước chảy được:

1:5 =1/5 (bể) = 20% (bể)

Vòi nước chảy 3 giờ thì chiếm được:

20% x 3= 60% (bể)

ko bt lm sao?!

Có tin t bảo cô m hỏi bài trên mạng không?

Mấy bài t hỏi là t đố con chính chủ xg con chính chủ nó đăng thôi

e)

\(\dfrac{x+2}{3}=\dfrac{3}{x+2}\\ =\left(x+2\right)^2=9\\ \left[{}\begin{matrix}x+2=3\\x+2=-3\end{matrix}\right.\\ \left[{}\begin{matrix}x=1\\x=-5\end{matrix}\right.\)

f)

\(\dfrac{x-4}{-5}=\dfrac{-5}{x-4}\\ \left(x-4\right)^2=25\\ \left[{}\begin{matrix}x-4=5\\x-4=-5\end{matrix}\right.\\ \left[{}\begin{matrix}x=9\\x=-1\end{matrix}\right.\)

\(\dfrac{x+2}{3}=\dfrac{3}{x+2}\\ =>\left(x+2\right)^2=9\\ =>\left[{}\begin{matrix}x+2=3\\x+2=-3\end{matrix}\right.=>\left[{}\begin{matrix}x=1\\x=-5\end{matrix}\right.\)

e)

x−4−5=−5x−4(x−4)2=25[x−4=5x−4=−5[x=9x=−1

\(\dfrac{-9}{11}\cdot\dfrac{3}{13}-\dfrac{9}{11}\cdot\dfrac{10}{13}+1\dfrac{9}{11}=\dfrac{-9}{11}\cdot\dfrac{3}{13}-\dfrac{9}{11}\cdot\dfrac{10}{13}+\dfrac{20}{11}=\dfrac{9}{11}\cdot\dfrac{-3}{13}-\dfrac{9}{11}\cdot\dfrac{10}{13}+\dfrac{20}{11}\cdot1=\dfrac{9}{11}\cdot\left(\dfrac{-3}{23}-\dfrac{10}{13}\right)+\dfrac{20}{11}=\dfrac{9}{11}\cdot\left(-1\right)+\dfrac{20}{11}=-\dfrac{9}{11}+\dfrac{20}{11}=\dfrac{11}{11}=1\)

=-9/11.3/13+-9/11.10/13+20/11
=-9/11.(3/13+10/13)+20/11

=-9/11.13/13+20/11

=-9/11.1+20/11

=-9/11+20/11

=(-9)+20/11

=11/11=1

\(\dfrac{2}{5}\cdot\dfrac{3}{7}-\dfrac{10}{7}+\dfrac{3}{7}\cdot\dfrac{3}{5}=\dfrac{3}{7}\cdot\left(\dfrac{2}{5}+\dfrac{3}{5}\right)-\dfrac{10}{7}=\dfrac{3}{7}\cdot\dfrac{5}{5}-\dfrac{10}{7}=\dfrac{3}{7}\cdot1-\dfrac{10}{7}=\dfrac{3}{7}-\dfrac{10}{7}=-\dfrac{7}{7}=-1\)

187/221

11/13

187/221