iúp mik bài này đi, mik cần gấp
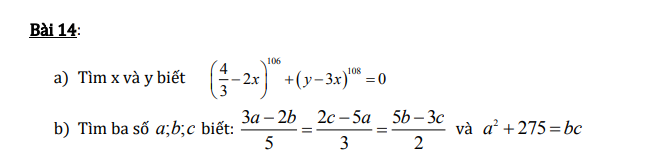

iúp mik với, mik đang cần gấp, các bạn làm nhanh giúp mik nhé, bạn nào nhanh nhất mik tặng tim
gọi d là ƯCLN(18n+3,21n+7)
ta có 18n+3chia hết cho d
21n+7 chia hết cho d
⇔21n+7-18n-3 chia hết cho d
⇔126n+42-126n-21 chia hết cho d
21 chia hết cho d
⇒d∈Ư(21)=1;3;7;21
n ≠ 3k-1;3k-3;3k-7;3k-21
mik đang cần bài này gấp các bạn giải hết bài giúp mik nhé mik cần gấp để nộp bài cho thầy
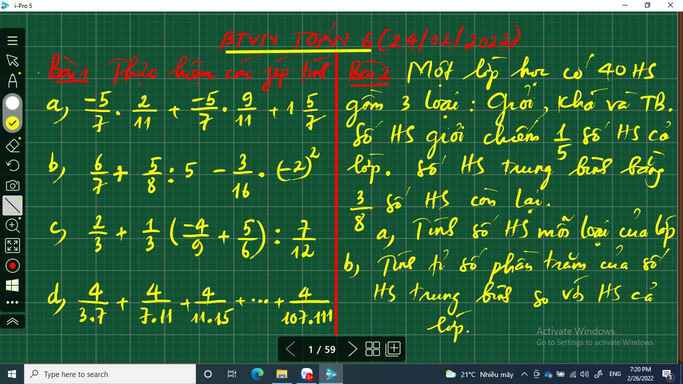
e tách câu hỏi ra nhe tạm thời cj giúp mụt câu nhe
a: \(=\dfrac{-5}{7}\left(\dfrac{2}{11}+\dfrac{9}{11}\right)+1+\dfrac{5}{7}=\dfrac{-5}{7}+1+\dfrac{5}{7}=1\)
b: \(=\dfrac{6}{7}+\dfrac{1}{8}-\dfrac{3}{16}\cdot4=\dfrac{6}{7}+\dfrac{1}{8}-\dfrac{3}{4}=\dfrac{13}{56}\)
c: \(=\dfrac{2}{3}+\dfrac{1}{3}\cdot\dfrac{-24+45}{54}\cdot\dfrac{12}{7}\)
\(=\dfrac{2}{3}+\dfrac{1}{3}\cdot\dfrac{21}{54}\cdot\dfrac{12}{7}=\dfrac{2}{3}+\dfrac{2}{9}=\dfrac{6+2}{9}=\dfrac{8}{9}\)
d: \(=\dfrac{1}{3}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{11}+...+\dfrac{1}{107}-\dfrac{1}{111}\)
\(=\dfrac{1}{3}-\dfrac{1}{111}=\dfrac{108}{333}=\dfrac{12}{37}\)
 Giúp mik bài này với ạ, mik cần gấp! Mik cảm ơn!!
Giúp mik bài này với ạ, mik cần gấp! Mik cảm ơn!!
Giúp mik mấy bài này vs mik cần gấp
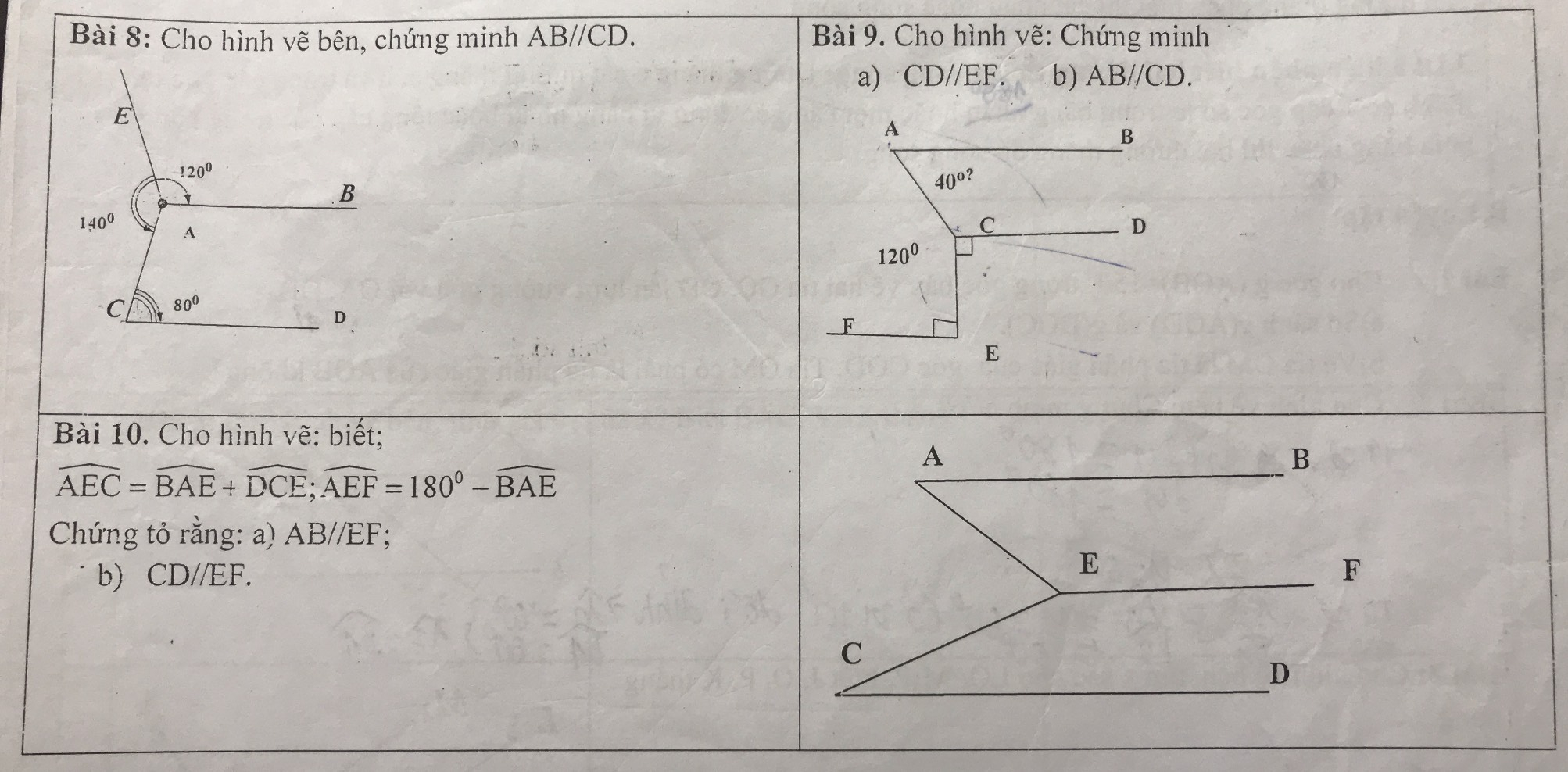
giúp mik bài này với ạ, mik cần gấp 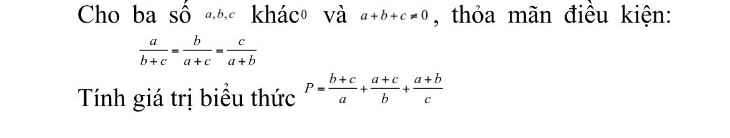
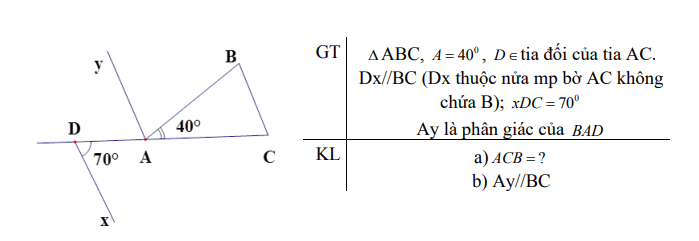
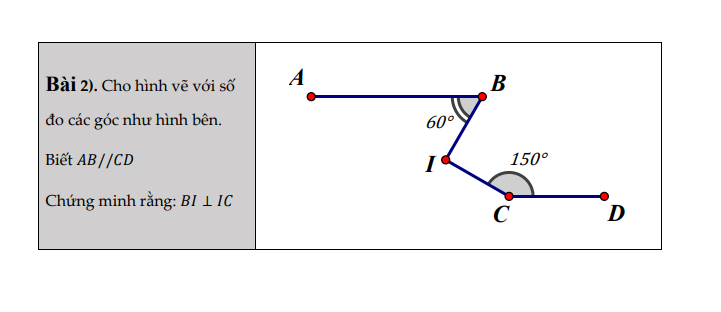
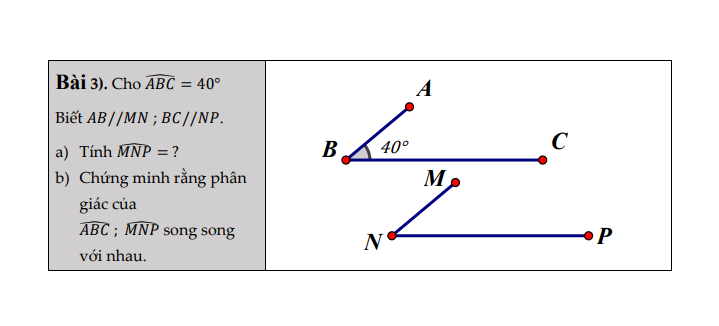
giúp mik ba bài này ik, mik cần gấp

giúp mik bài này với mik đang cần gấp
\(\left(xy+3\right)^2+\left(x+y\right)^2=8\)
\(\Leftrightarrow x^2y^2+x^2+y^2+1=-8xy\)
\(\dfrac{x}{x^2+1}+\dfrac{y}{y^2+1}=-\dfrac{1}{4}\Leftrightarrow\dfrac{\left(xy+1\right)\left(x+y\right)}{x^2y^2+x^2+y^2+1}=-\dfrac{1}{4}\)
\(\Rightarrow\dfrac{\left(xy+1\right)\left(x+y\right)}{-8xy}=-\dfrac{1}{4}\)
\(\Rightarrow\left(xy+1\right)\left(x+y\right)=2xy\)
\(\Rightarrow x+y=\dfrac{2xy}{xy+1}\)
Thế vào pt ban đầu:
\(\left(xy+3\right)^2+\left(\dfrac{2xy}{xy+1}\right)^2=8\)
Đặt \(xy+1=t\Rightarrow\left(t+2\right)^2+4\left(\dfrac{t-1}{t}\right)^2=8\)
\(\Rightarrow\left(t^2+2t\right)^2-4\left(t^2+2t\right)+4=0\)
\(\Leftrightarrow\left(t^2+2t-2\right)^2=0\)
\(\Rightarrow\left[{}\begin{matrix}t=-1-\sqrt{3}\\t=-1+\sqrt{3}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}xy=-2-\sqrt{3}\Rightarrow x+y=1+\sqrt{3}\\xy=-2+\sqrt{3}\Rightarrow x+y=1-\sqrt{3}\end{matrix}\right.\)
\(\Rightarrow x;y\) là nghiệm của: \(\left[{}\begin{matrix}X^2-\left(1+\sqrt{3}\right)X-2-\sqrt{3}=0\\X^2-\left(1-\sqrt{3}\right)X-2+\sqrt{3}=0\end{matrix}\right.\)
\(\Rightarrow...\)
Giúp mik bài này vs ạ mik đang cần gấp
b: Xét ΔABE vuông tại A có AH là đường cao ứng với cạnh huyền BE
nên \(BH\cdot BE=AB^2\left(1\right)\)
Xét ΔABC vuông tại B có BH là đường cao ứng với cạnh huyền AC
nên \(AH\cdot AC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BH\cdot BE=AH\cdot AC\)
mn ơi giúp mik bài này với, mik cần gấp ! 