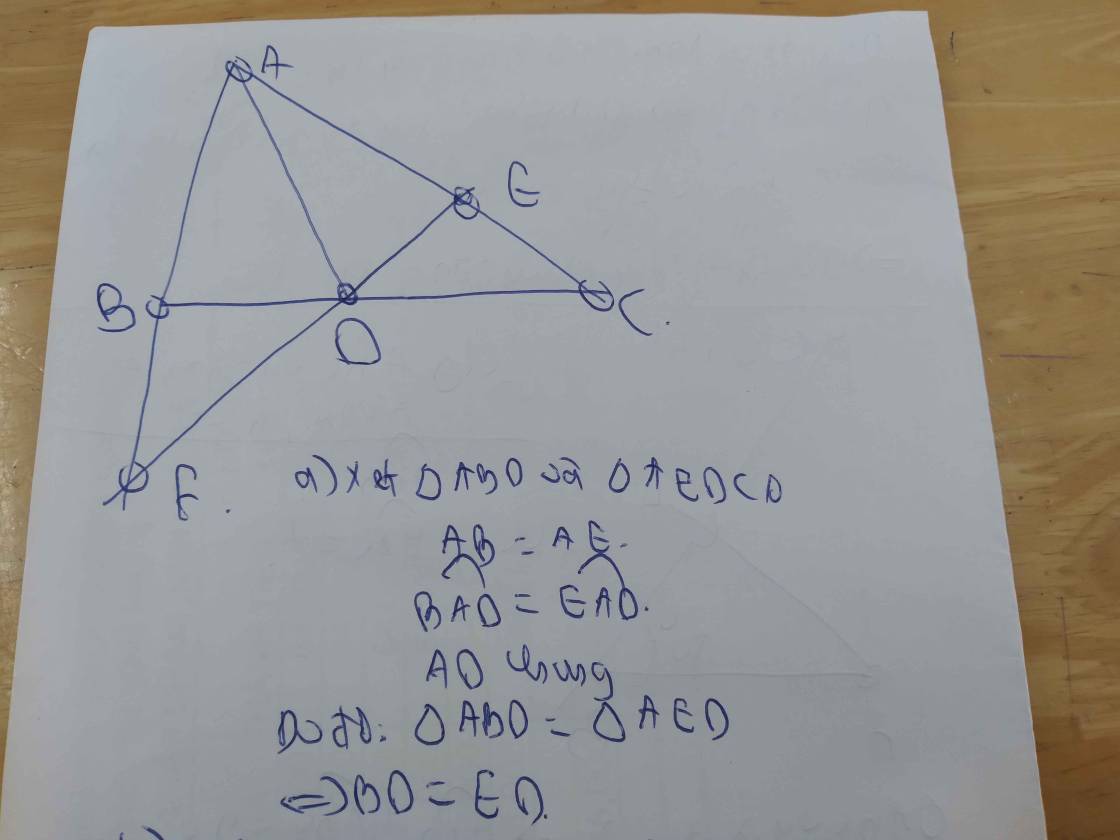
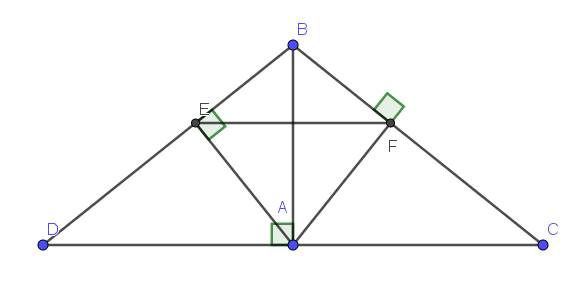
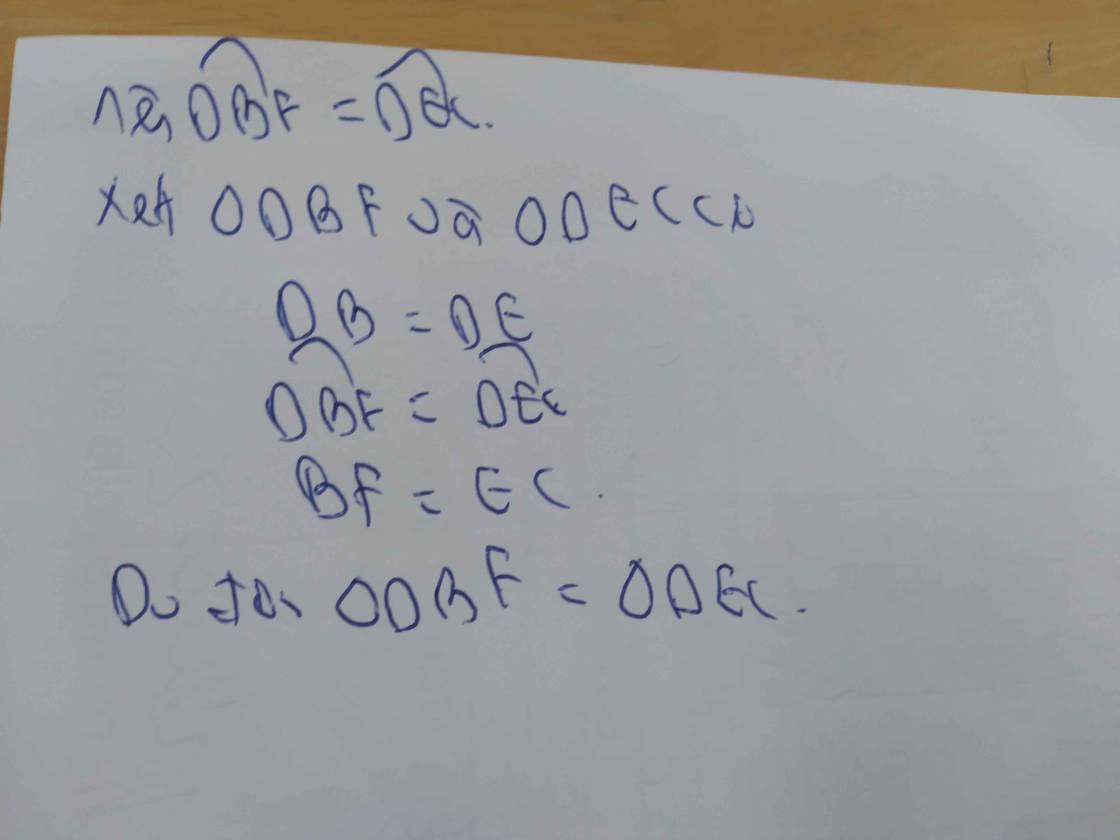Cho ABC có AB < AC. Kẻ tia phân giác AD của góc BAC (D thuộc BC). Trên
cạnh AC lấy điểm E sao cho AE = AB, trên tia AB lấy điểm F sao cho AF = AC. Chứng
minh rằng:
a. ∆ABD = ∆AED b. BF = EC.
c. ∆ABE cân và AD là trung trực của BE.
d) BE//CF.
Chương II : Tam giác
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
b: ΔABD=ΔAED
=>DB=DE
Ta có: AB+BF=AF
AE+EC=AC
mà AB=AE và AF=AC
nên BF=EC
c: Xét ΔABE có AB=AE
nên ΔABE cân tại A
ΔABE cân tại A
mà AD là đường phân giác
nên AD là đường trung trực của BE
d: Xét ΔAFC có \(\dfrac{AB}{BF}=\dfrac{AE}{EC}\)
nên BE//FC
Đúng 2
Bình luận (0)
Cho tam giác MNP nhọn có MN < MP. Trên cạnh MP lấy điểm B sao cho MB = MN. Lấy O là trung điểm của NB. Chứng minh ba điểm B, A, C thẳng hàng.
(Em vẽ thừa điểm F ạ)
Chứng minh rằng trong một tam giác độ dài cạnh lớn nhất sẽ lớn hơn hoặc bằng chu vi của tam giác nhưng nhỏ hơn
Em xem lại đề vì trong một tam giác độ dài một cạnh luôn nhỏ hơn tổng hai cạnh còn lại
⇒ Độ dài cạnh đó nhỏ hơn chu vi của tam giác
Đúng 0
Bình luận (0)
Bài 6 cho tam giác ABC , AD là tia phân giác BAC, AB = AC
A} chứng minh tam giác ABD = tam giác ACD
B} chứng minh AD cắt BC
C} chứng minh D là trung điểm BC
D} tia đối BC lấy E , tia đối CB lấy F,BF = CF, chứng minh tam giác ABE = ACF
ai giải giúp mk với mai mk ôn thi rồi
a: Xét ΔADB và ΔADC có
AD chung
\(\widehat{BAD}=\widehat{CAD}\)
AB=AC
Do đó: ΔADB=ΔADC
b: Ta có: ΔADB=ΔADC
=>\(\widehat{ADB}=\widehat{ADC}\)
mà \(\widehat{ADB}+\widehat{ADC}=180^0\)(hai góc kề bù)
nên \(\widehat{ADB}=\widehat{ADC}=\dfrac{180^0}{2}=90^0\)
=>AD\(\perp\)BC
c: ta có: ΔABD=ΔACD
=>DB=DC
=>D là trung điểm của BC
d: ta có: \(\widehat{ABE}+\widehat{ABC}=180^0\)(hai góc kề bù)
\(\widehat{ACF}+\widehat{ACB}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
nên \(\widehat{ABE}=\widehat{ACF}\)
Xét ΔABE và ΔACF có
AB=AC
\(\widehat{ABE}=\widehat{ACF}\)
BE=CF
Do đó: ΔABE=ΔACF
Đúng 1
Bình luận (2)
Cho tam giác ABC cân tại A kẻ BD vuông góc với AC và CE vuông góc với AB gọi I là giao điểm của BD và EC câu a chứng minh BE = CD CÂU B chứng minh AI là tia phân giác CỦA GÓC DAC COI C CHỨNG MINH TAM GIÁC BIC LÀ TAM GIÁC GÌ VÌ SAO .GIÚP VỚI PLS
a: Xét ΔEBC vuông tạiE và ΔDCB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)(ΔABC cân tại A)
Do đó: ΔEBC=ΔDCB
=>EB=DC
b: Sửa đề; AI là phân giác của góc BAC
Ta có: AE+EB=AB
AD+DC=AC
mà EB=DC và AB=AC
nên AE=AD
Xét ΔAEI vuông tại E và ΔADI vuông tại D có
AI chung
AE=AD
Do đó: ΔAEI=ΔADI
=>\(\widehat{EAI}=\widehat{DAI}\)
=>AI là phân giác của góc DAE
c: Ta có: ΔAEI=ΔADI
=>IE=ID
Xét ΔIEB vuông tạiE và ΔIDC vuông tại D có
IE=ID
EB=DC
Do đó: ΔIEB=ΔIDC
=>IB=IC
=>ΔIBC cân tại I
Đúng 1
Bình luận (0)
Bài 2: Cho tam giác ABC có AB < AC. Kẻ tia phân giác AD của góc BAC (D thuộc BC) Trên cạnh AC lấy điểm E sao cho AE = AB, trên tia AB lấy điểm F sao cho AF = AC
Chứng minh rằng:
a) BD = ED
b) BF = EC
c) Tam giác BDF = tam giác EDC
d) AD vuông góc DC
Cho tam giác abc cân AAB hơn 90 độ góc KBD và CE cắt nhau tại i chứng minh rằng
a) AEC=ADB
b)AI là tia phân giác của góc A
c) ED//BC
a: Xét ΔBAC vuông tại A và ΔBAD vuông tại A có
BA chung
AC=AD
Do đó;ΔBAC=ΔBAD
b: Ta có: ΔBAC=ΔBAD
=>\(\widehat{ABC}=\widehat{ABD}\)
Xét ΔBEA vuông tại E và ΔBFA vuông tại F có
BA chung
\(\widehat{EBA}=\widehat{FBA}\)
Do đó: ΔBEA=ΔBFA
=>AE=AF
=>ΔAEF cân tại A
c: ta có: ΔBEA=ΔBFA
=>BE=BF
Xét ΔBDC có \(\dfrac{BE}{BD}=\dfrac{BF}{BC}\)
nên EF//DC
Đúng 0
Bình luận (0)
Lời giải:
a.
Tam giác $ABC$ vuông tại $A\Rightarrow \widehat{BAC}=90^0$
$\widehat{BAD}=180^0-\widehat{BAC}=180^0-90^0=90^0$
Xét tam giác $ABC$ và $ABD$ có:
$AB$ chung
$\widehat{BAC}=\widehat{BAD}=90^0$
$AD=AC$ (gt)
$\Rightarrow \triangle ABC=\triangle ABD$ (c.g.c)
b.
Từ tam giác bằng nhau phần a
$\Rightarrow \widehat{DBA}=\widehat{CBA}$
$\Rightarrow \widehat{EBA}=\widehat{FBA}$
Xét tam giác $EBA$ và $FBA$ có:
$\widehat{EBA}=\widehat{FBA}$ (cmt)
$\widehat{BEA}=\widehat{BFA}=90^0$
$BA$ chung
$\Rightarrow \triangle EBA=\triangle FBA$ (ch-gn)
$\Rightarrow EA=FA$
$\Rightarrow AEF$ cân tại $A$.
c.
Từ tam giác bằng nhau phần b
$\Rightarrow BE=BF, AE=AF$
$\Rightarrow BA$ là trung trực của $EF$
$\Rightarrow BA\perp EF$
Mà $BA\perp DC$
$\Rightarrow EF\parallel DC$
Đúng 1
Bình luận (0)
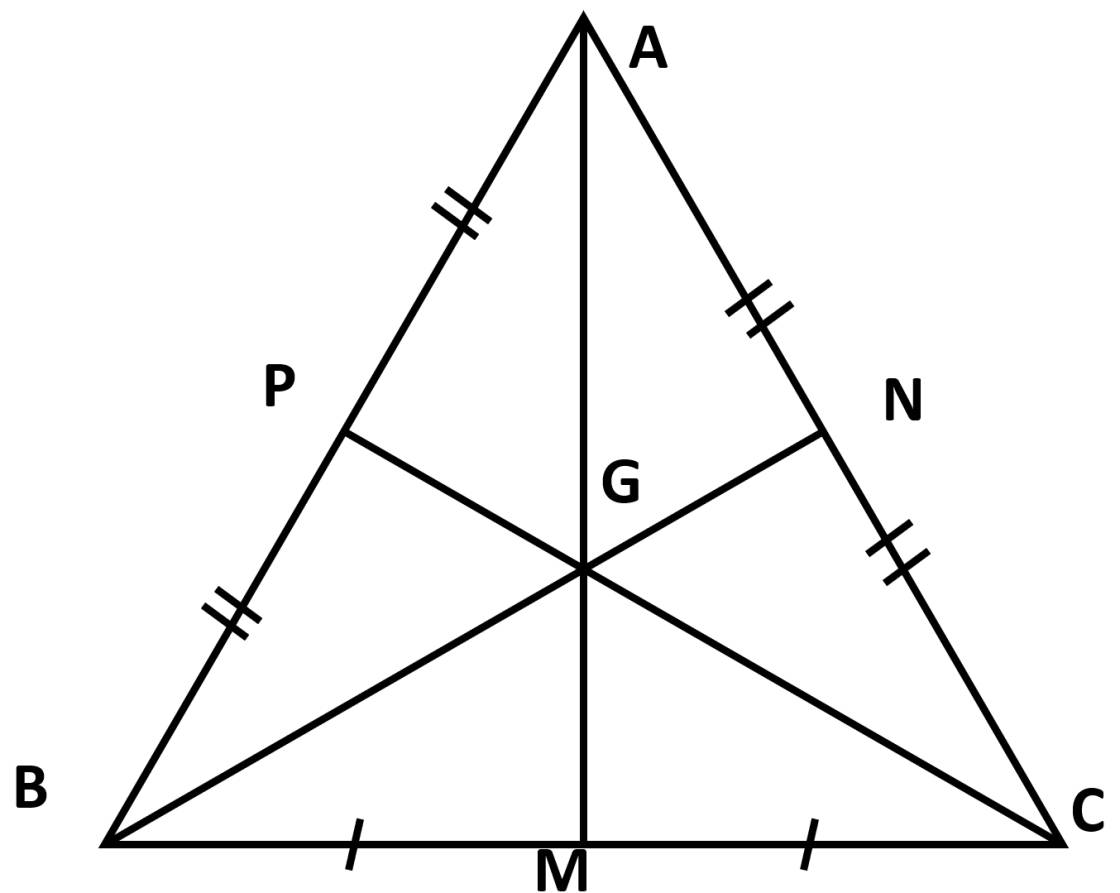
cho tam giác ABC cân ở A,AM=12cm và 3 trung tuyến AM,BN,CP đồng quy tại trọng tâm G
a) tính AG b)chứng minhAM vuông góc BC
c)chứng minh AM là tia phân giác của góc BAC.
d) cho BG= 6cm. Tính độ dài đoạn thẳng CF ?
a) vì G là trọng tâm của \(\Delta ABC\) nên ta có:
\(AG=\dfrac{2}{3}\cdot AM=\dfrac{2}{3}\cdot12=8\left(cm\right)\)
b) ta có AM là đường trung tuyến của ΔABC
lại có: ΔABC là Δ cân
⇒ AM cũng là đường cao của ΔABC
⇒ AM ⊥ BC
c) ta có AM là đường trung tuyến của ΔABC
lại có: ΔABC là Δ cân
⇒ AM cũng là đường phân giác của ΔABC
⇒ AM là tia phân giác của \(\widehat{BAC}\)
d) ta có: \(AB=AC\) (vì ΔABC cân tại A)
\(\Rightarrow\dfrac{1}{2}\cdot AB=\dfrac{1}{2}\cdot AC=PB=NC\)
Xét △PBC và △NCB, có:
PB = NC (cmt)
\(\widehat{ABC}=\widehat{ACB}\) (Vì △ABC cân tại A)
BC là cạnh chung
⇒ △PBC và △NCB (c-g-c)
⇒ PC = BN (2 cạnh tương ứng)
độ dài cạnh BN là:
\(6:\dfrac{2}{3}=9\left(cm\right)\)
CP = BN = 9 (cm)
vậy cạnh CP = 9cm
Đúng 1
Bình luận (0)
Cho ▲ABC có 3 góc nhọn . Gọi M là trung điểm AC trên BH lấy D sao cho BM=MD
a)Chứng minh ▲MAB=▲MCD
b)Lấy I thuộc đoạn thẳng BC (I#BC).Qua D kẻ đường thẳng // BC cắt tia IH tại N , Chứng minh M lag trung điểm IN