Bạn tham khảo:

Tìm m để hàm số : \(y=\sqrt{\frac{m-\sin x-\cos x-2\sin x\cos x}{\sin^{2017}x-\cos^{2019}x \sqrt{2}}}\) xác định với mọi... - Hoc24

Ủa sao xài hoành độ đỉnh ở đây được nhỉ, phải xài nghiệm (đúng hơn là lợi dụng quy tắc dấu tam thức bậc 2 "trong khác - ngoài cùng")

Đây, ví dụ 1 trường hợp cho em (bài này ở trên đã đưa dấu a>0 theo thói quen). 2 đường màu đỏ là khoảng \(\left(-1;\dfrac{1}{2}\right)\), rõ ràng đỉnh parabol nằm trong khoảng đó nhưng trên khoảng \(\left(-1;\dfrac{1}{2}\right)\) hàm vẫn có 1 đoạn nhận giá trị dương (tương ứng với đoạn BC)

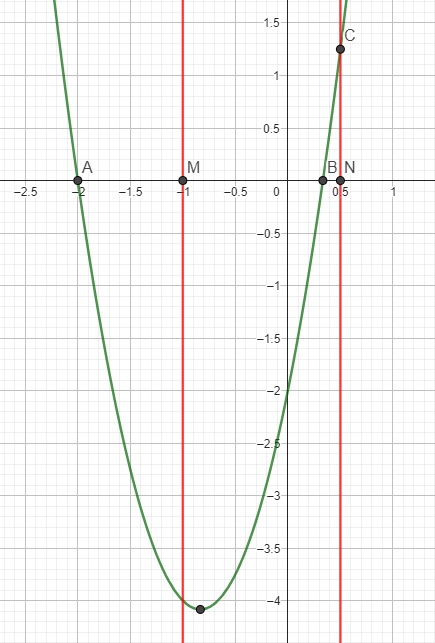
Cách làm đúng ở đây là cần sử dụng quy tắc tam thức bậc 2  (hoặc 1 số pp khác nhưng ko thể là hoành độ đỉnh). Lợi dụng quy tắc tam thức bậc 2: nếu pt bậc 2 có 2 nghiệm \(x_1;x_2\) thì \(a.f\left(x\right)< 0\) với \(x\in\left(x_1;x_2\right)\) và \(a.f\left(x\right)>0\) với \(x\notin\left(x_1;x_2\right)\).

Do đó để  \(f\left(x\right)< 0\) ; \(\forall x\in\left(p;q\right)\) nào đó (khi a dương), đồng nghĩa khi đó p và q phải nằm giữa 2 nghiệm, hay \(f\left(p\right)\) và \(f\left(q\right)\) đều âm.

Hàm xác định trên khoảng đã cho khi và chỉ khi:

\(4\left(sin^6x+cos^6x\right)-6m.sin2x+2-m^2\ge0;\forall x\in\left(...\right)\)

\(\Leftrightarrow4\left[\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)\right]-6m.sin2x+2-m^2\ge0;\forall x\in...\)

\(\Leftrightarrow-3sin^22x-6m.sin2x-m^2+6\ge0\)

Đặt \(sin2x=t\Rightarrow t\in[-1;\dfrac{1}{2})\)

\(\Rightarrow f\left(t\right)=3t^2+6mt+m^2-6\le0\)

Theo định lý về dấu của tam thức bậc 2 thì điều này xảy ra khi và chỉ khi:

\(\left\{{}\begin{matrix}f\left(-1\right)\le0\\f\left(\dfrac{1}{2}\right)< 0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m^2-6m-3\le0\\m^2+3m-\dfrac{21}{4}< 0\end{matrix}\right.\)

Ủa biến đổi có sai ở đâu ko mà BPT cuối nhìn nghiệm xấu vậy

a.

\(y'=\dfrac{3}{cos^2\left(3x-\dfrac{\pi}{4}\right)}-\dfrac{2}{sin^2\left(2x-\dfrac{\pi}{3}\right)}-sin\left(x+\dfrac{\pi}{6}\right)\)

b.

\(y'=\dfrac{\dfrac{\left(2x+1\right)cosx}{2\sqrt{sinx+2}}-2\sqrt{sinx+2}}{\left(2x+1\right)^2}=\dfrac{\left(2x+1\right)cosx-4\left(sinx+2\right)}{\left(2x+1\right)^2}\)

c.

\(y'=-3sin\left(3x+\dfrac{\pi}{3}\right)-2cos\left(2x+\dfrac{\pi}{6}\right)-\dfrac{1}{sin^2\left(x+\dfrac{\pi}{4}\right)}\)

a: Để hàm số đồng biến trên R thì \(m^2-4>0\)

=>\(m^2>4\)

=>\(\left[{}\begin{matrix}m>2\\m< -2\end{matrix}\right.\)

b: Để hàm số nghịch biến trên R thì \(m^2-4< 0\)

=>\(m^2< 4\)

=>-2<m<2

a) Hàm số y = (3m - 1)x + 2 với m  1313 

Vậy m >  nghịch biến

⇔ 3m - 1 < 0

⇔ 3m < 1

⇔ m < 1313 thì hàm số y = (3m - 1)x + 2 nghịch biến

c) Đồ thị hàm số y = (3m - 1)x + 2 với m  )

⇔ 3 = 6m - 2 + 2

⇔ 3 = 6m

⇔ m = 1212 thì đồ thị hàm số y = (3m - 1)x + 2 đi qua điểm A(2; 3)

a) Hàm số đồng biến khi:

m² - 4 > 0

⇔ m² > 4

⇔ m < -2 hoặc m > 2

Vậy m < -2; m > 2 thì hàm số đồng biến

b) Hàm số nghịch biến khi:

m² - 4 < 0

⇔ m² < 4

⇔ -2 < m < 2

Vậy -2 < m < 2 thì hàm số nghịch biến

a: Để hàm số là hàm số bậc nhất thì m-2>0

hay m>2

b: Để hàm số là hàm số bậc nhất thì \(\left(m-1\right)\left(m+1\right)>0\)

hay \(\left[{}\begin{matrix}m>1\\m< -1\end{matrix}\right.\)

`TXĐ: R`

Ta có: `-1 <= sin(x+ \pi/3) <= 1`

`<=>0 <= sin^4 (x+\pi/3) <= 1`

`<=>2 <= y <= 3`

    `=>y_[mi n]=2<=>sin(x +\pi/3)=0<=>x= -\pi/3+k\pi`   `(k in ZZ)`

        `y_[max]=3<=>sin(x +\pi/3)=1<=>x=\pi/6 +k2\pi`  `(k in ZZ)`