Chứng minh rằng : sinx=x-1 có ít nhất một nghiệm
GS
Những câu hỏi liên quan
Chứng minh rằng phương trình cos2x = sinx − 2 có ít nhất hai nghiệm trong khoảng - π 6 ; π
Xét f(x) = cos2x - sinx + 2 trên các khoảng
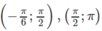
Đúng 0
Bình luận (0)
Chứng minh phương trình \(sin^3x+sinx-1=0\) có ít nhất 1 nghiệm.
Đặt \(f\left(x\right)=sin^3x+sinx-1\)
Hàm \(f\left(x\right)\) liên tục trên R
Ta có: \(f\left(0\right)=-1\) ; \(f\left(\dfrac{\pi}{2}\right)=1\)
\(\Rightarrow f\left(0\right).f\left(\dfrac{\pi}{2}\right)< 0\)
\(\Rightarrow\) Phương trình \(f\left(x\right)=0\) luôn có ít nhất 1 nghiệm thuộc \(\left(0;\dfrac{\pi}{2}\right)\) (đpcm)
Đúng 2
Bình luận (0)
Chứng minh rằng phương trình sau có ít nhất một nghiệm: sin x = x – 1 .
a) Cho f(x) thỏa mãn: x.f(x-2) = (x-4) f(x)
Chứng minh rằng: Đa thức có ít nhất 2 nghiệm
b) Biết (x-1) . f(x) = (x+4) . f(x+8) với mọi x
Chứng minh rằng: f(x) có ít nhất 2 nghiệm
Chứng minh rằng phương trình sau có ít nhất hai nghiệm: 2 x 3 - 5 x 2 + x + 1 = 0
Chứng minh rằng phương trình sau có ít nhất hai nghiệm :
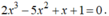
- Xét hàm số: f ( x ) = 2 x 3 - 5 x 2 + x + 1 là hàm đa thức.
⇒ Hàm số f liên tục trên R.
- Ta có:
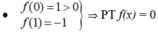 có ít nhất một nghiệm c1 ∈ (0;1).
có ít nhất một nghiệm c1 ∈ (0;1).
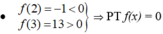 có ít nhất một nghiệm c2 ∈ (2;3).
có ít nhất một nghiệm c2 ∈ (2;3).
- Mà c ≠ c 2 nên PT f(x) = 0 có ít nhất 2 nghiệm.
Đúng 0
Bình luận (0)
Chứng minh rằng: P(x) có ít nhất 2 nghiệm
x.P(x+1)=(x-2).P(x)
chứng minh rằng phương trình (m²-m+1)x⁴-2x³-1=0 có ít nhất 2 nghiệm /(-5;5)
Đặt \(f\left(x\right)=\left(m^2-m+1\right)x^4-3x^3-1\)
\(f\left(x\right)\) là hàm đa thức nên liên tục trên mọi khoảng trên R
\(f\left(0\right)=-1< 0\)
\(f\left(3\right)=81\left(m^2-m+1\right)-55=81\left(m-\dfrac{1}{2}\right)^2+\dfrac{23}{4}>0\)
\(\Rightarrow f\left(0\right).f\left(3\right)< 0\Rightarrow\) pt có ít nhất 1 nghiệm thuộc \(\left(0;3\right)\)
\(f\left(-1\right)=m^2-m+2=\left(m-\dfrac{1}{2}\right)^2+\dfrac{7}{4}>0\)
\(\Rightarrow f\left(-1\right).f\left(0\right)< 0\Rightarrow\) pt có ít nhất 1 nghiệm thuộc \(\left(-1;0\right)\)
\(\Rightarrow\) Pt có ít nhất 2 nghiệm thuộc \(\left(-1;3\right)\Rightarrow\) có ít nhất 2 nghiệm trên \(\left(-5;5\right)\)
Đúng 2
Bình luận (0)
Chứng minh rằng đa thức f(x) có ít nhất 2 nghiệm biết rằng: x. f(x+1) = (x+3). f(x)
Vì x f(x+1) = (x+3)f(x) với mọi x nên:
* khi x=0 thì 0.f(0-1) = (0+3).f(0) tương đương f(0)=0. vậy 0 là nghiệm của đa thức f(x)
* khi x=-3 suy ra -3.f(-3+2) = (-3 +3). f(-3)
-3f(-2) = 0f(-3) tuong duong f(-2) = 0. vậy -2 cũng là một nghiệm của f(x)
do đó đa thức f(x) có ít nhất 2 nghiệm là 0 và 2
Đúng 0
Bình luận (0)
từ pt x.f(x+1) = f( x+ 2) .f(x)
xét x= 0
pt có dạng 0= f(2).f(0)
vậy hoặc f(2) = 0 hoặc f(0) = 0
hay hoặc x= 2 hoặc x= 0 là nghiệm của pt f(x) = 0
KL pt f(x) = 0 có ít nhất 2 nghiệm
Đúng 0
Bình luận (0)
Cho x. f(x)=(x-1).f(x+1)
CM: f(x) có ít nhất 2 nghiệm
Đúng 0
Bình luận (0)
1.Chứng minh rằng đa thức P(x) có ít nhất hai nghiệm biết rằng:
x.P(x +2) – (x -3).P(x -1) = 0
Với x = 0 Ta có:
0.P(0 + 2) – (0 – 3).P(0 – 1) = 0 ⇔ 0 + 3P(-1) = 0 ⇔ P(-1) =0
=> x = -1 là nghiệm của đa thức P(x)
Với x = 3 ta có:
3.P(3 + 2) – (3 – 3) .P(3 – 1) = 0 ⇔ 3.P(5) – 0.P(2) = 0
⇔ 3.P(5) = 0 ⇔ P(5) = 0
=> x = 5 là nghiệm của đa thức P(x)
Vậy đa thức P(x) có ít nhất 2 nghiệm là -1 và 0.
Đúng 0
Bình luận (2)
vậy đa thức P(x) có ít nhất 2 nghiệm là : -1 và 5 chứ Phùng Khánh Linh ....
Đúng 0
Bình luận (0)
Với x = 0 Ta có:
0.P(0 + 2) – (0 – 3).P(0 – 1) = 0 ⇔ 0 + 3P(-1) = 0 ⇔ P(-1) =0
=> x = -1 là nghiệm của đa thức P(x)
Với x = 3 ta có:
3.P(3 + 2) – (3 – 3) .P(3 – 1) = 0 ⇔ 3.P(5) – 0.P(2) = 0
⇔ 3.P(5) = 0 ⇔ P(5) = 0
=> x = 5 là nghiệm của đa thức P(x)
Vậy đa thức P(x) có ít nhất 2 nghiệm là -1 và 0.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời


