Từ đỉnh C của ΔABC nhọn, kẻ đường cao CH; kẻ HM ⊥ BC, HN ⊥ AC. CM: ΔMNC đồng dạng với ΔABC
TP
Những câu hỏi liên quan
* Cho ΔABC vuông tại A, biết AC= 12cm, BC=15cm
a. Giải tam giác ABC
b. Tính độ dài đường cao AH, đường phân giác AD của ΔABC
* Cho ΔABC có 3 góc nhọn, kẻ đường cao AH.
a. CM: sinA+cos A>1
b. CM: BC=AH. (cotgB+cotgC)
c. Biết AH=6cm, góc B=\(60^0\), góc C=\(45^0\). Tính diện tích ΔABC
Bài 2:
b: \(AH\cdot\left(\cot\widehat{B}+\cot\widehat{C}\right)\)
\(=AH\cdot\left(\dfrac{BH}{AH}+\dfrac{CH}{AH}\right)\)
\(=AH\cdot\dfrac{BC}{AH}=BC\)
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC, 3 đường cao AD;BE;CF gặp nhau tại H qua 3 đỉnh A,F. Kẻ 3 đường thẳng // BC ; AC, chúng cắt nhau tại M,N. CMR H cách đều 3 đỉnh của Tam giác .
Cho tam giác nhọn ABC, 3 đường cao AD;BE;CF gặp nhau tại H qua 3 đỉnh A,F. Kẻ 3 đường thẳng // BC ; AC, chúng cắt nhau tại M,N. CMR H cách đều 3 đỉnh của Tam giác .
Cho ΔABC nhọn, kẻ đường cao BD và CE, vẽ các đường cao DF và EG của ΔADE. Chọn khẳng định đúng?
A. AD.AE = AB.AF
B. AD.AE = AB.AG = AC.AF
C. AD.AE = AC.GA
D. AD.AE = AB.AF = AC.AG
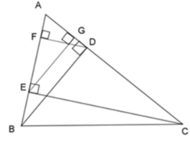
Từ câu trước ta có: A E A B = A G A D => AE.AD = AB.AG (1)
Chứng minh tương tự, ta được: ΔAFD ~ ΔAEC (c - c - c)
=> => AF.AC = AE.AD (2)
Từ (1) và (2) ta có: AD.AE = AB.AG = AC.AF
Đáp án: B
Đúng 0
Bình luận (0)
Cho ΔABC nhọn, kẻ đường cao BD và CE, vẽ các đường cao DF và EG của ΔADE. Chọn khẳng định không đúng?
A. AD.AE=AB.AG
B. AD.AE = AC.AF
C. AD.AE = AC.FD
D. AE.EG = AB.BD
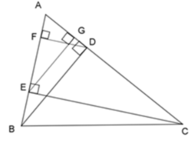
Từ câu trước ta có: A E A B = A G A D = E G B D => AE.AD = AB.AG (1) nên A đúng
Chứng minh tương tự, ta được: ΔAFD ~ ΔAEC (c - c - c)
=> A F A E = A D A C => AF.AC = AE.AD (2) nên B đúng
Ngoài ra A D A C = F D E C => AD.EC = AC.FD nên C đúng
Chỉ có đáp án D sai vì A E E G = A B B D
Đáp án: D
Đúng 0
Bình luận (0)
Cho ΔABC nhọn, kẻ đường cao BD và CE, vẽ các đường cao DF và EG của ΔADE. ΔABD đồng dạng với tam giác nào dưới đây?
A. ΔAEG
B. ΔABC
C. Cả A và B
D. Không có tam giác nào
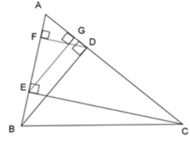
Xét ΔABD và ΔAEG, ta có:
BD ⊥ AC (BD là đường cao)
EG ⊥ AC (EG là đường cao)
=> BD // EG
Theo định lý Talet, ta có: A E A B = A G A D = E G B D
=> ΔAEG đồng dạng ΔABD (c - c - c) (đpcm)
Đáp án: A
Đúng 0
Bình luận (0)
Cho ΔABC nhọn (AB < AC). BD, CE là đường cao. Phân giác kẻ từ A của ΔABC cắt DE và BC lần lượt tại M, N. Giả sử \(AD=\frac{1}{2}AB\). Chứng minh : M là trung điểm của AN.
Giúp hộ !!! Thanks !
Xét \(\Delta ABD\)và \(\Delta ACE\)có:
\(\widehat{ADB}=\widehat{AEC}=90^o\); \(\widehat{BAC}\)( chung )
\(\Rightarrow\)\(\Delta ABD\approx\Delta ACE\left(g.g\right)\)
\(\Rightarrow\)\(\frac{AB}{AC}=\frac{AD}{AE}\)
Xét \(\Delta ADE\)và \(\Delta ABC\)có :
\(\frac{AB}{AC}=\frac{AD}{AE}\); \(\widehat{BAC}\)( chung )
\(\Rightarrow\Delta ADE\approx\Delta ABC\left(c.g.c\right)\)
\(\Rightarrow\widehat{D_1}=\widehat{ABC}\)
Xét \(\Delta ADM\)và \(\Delta ABN\)có :
\(\widehat{D_1}=\widehat{ABN}\); \(\widehat{A_1}=\widehat{A_2}\)
\(\Rightarrow\Delta ADM\approx\Delta ABN\left(g.g\right)\)
\(\Rightarrow\frac{AD}{AB}=\frac{AM}{AN}=\frac{1}{2}\)
Vậy M là trung điểm AN
Đúng 0
Bình luận (0)
Cho ΔABC nhọn, kẻ đường cao BD và CE, vẽ các đường cao DF và EG của ΔADE. Xét các cặp tam giác sau đây, số cặp tam giác đồng dạng với nhau là:
(1) ΔAEG và ΔABD
(2) ΔADF và ΔACE
(3) ΔABC và ΔAEC
A. 1
B. 0
C. 2
D. 3

Xét ΔABD và ΔAEG, ta có:
BD ⊥ AC (BD là đường cao)
EG ⊥ AC (EG là đường cao)
=> BD // EG
Theo định lý Talet, ta có: A E A B = A G A D = E G B D
=> ΔAEG ~ ΔABD (c - c - c) nên (1) đúng.
Tương tự ta cũng chứng minh được ΔADF ~ ΔACE nên (2) đúng
Dễ thấy (3) sai vì A E A B ≠ A C A C
Vậy có hai cặp tam giác đồng dạng trong các cặp đã nêu.
Đáp án: C
Đúng 0
Bình luận (0)
Cho ΔABC. Đường thẳng kẻ qua đỉnh B song song với AC. Đường thẳng kẻ qua đỉnh C song song với AB cắt nhau tại D và cắt đường thẳng kẻ qua đỉnh A song song với BC theo thứ tự ở E và F.
a) CM ΔABC = ΔBAE
b) Tính chu vi ΔDEF biết chu vi ΔABC =15cm
a, vì BD song song với AC nên góc B2 bằng góc C2. tương tự được góc C1 bằng góc B1.Do đó tam giác ABC = tam giác BAE(g.c.g) (dpcm)
b, vì AC song song với BD nên góc D bằng góc ACF.
vì AF song song với BC nên góc C1= góc CAF = B2.
theo câu a, tam giác ABC= tam giác DCB nên AC=BD, AB=DC
Do đó tam giác BDC=tam giác ACF(g.c.g) nên DC = CF=AB nên DF= DC+CF=2.AB.
Tương tự ta đc; DE=2.AC, EF=2.BC
Do đó Chu vi tam giác DEF bằng 2 lần chu vi tam giác ABC và bằng 30 cm
Đúng 0
Bình luận (1)
a, vì BD song song với AC nên góc B2 bằng góc C2. tương tự được góc C1 bằng góc B1.Do đó tam giác ABC = tam giác BAE(g.c.g) (dpcm)
b, vì AC song song với BD nên góc D bằng góc ACF.
vì AF song song với BC nên góc C1= góc CAF = B2.
theo câu a, tam giác ABC= tam giác DCB nên AC=BD, AB=DC
Do đó tam giác BDC=tam giác ACF(g.c.g) nên DC = CF=AB nên DF= DC+CF=2.AB.
Tương tự ta đc; DE=2.AC, EF=2.BC
Do đó Chu vi tam giác DEF bằng 2 lần chu vi tam giác ABC và bằng 30 cm
Đúng 0
Bình luận (0)


