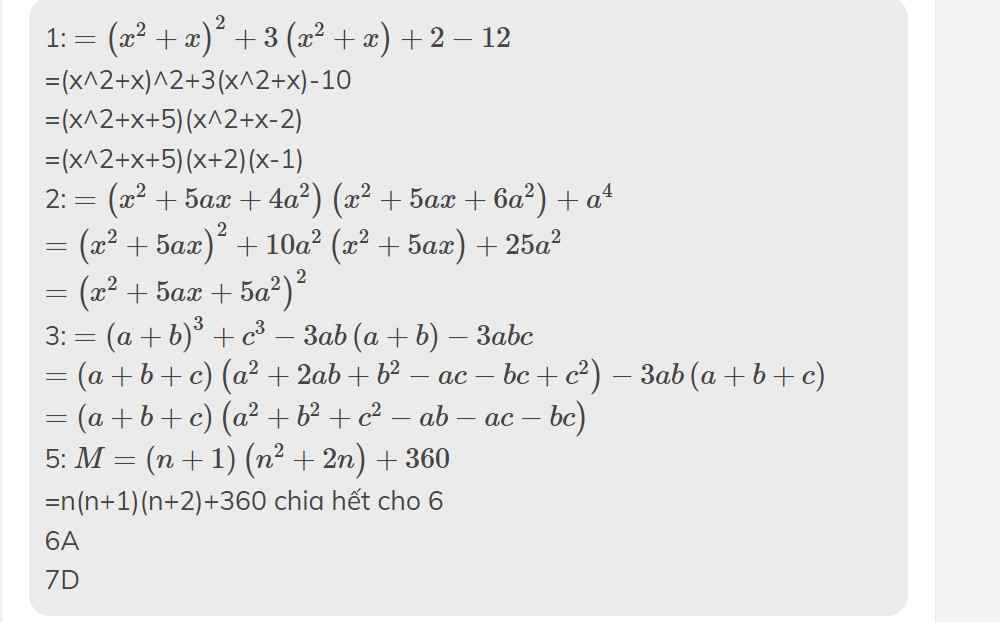\(\left|x-2\right|\)=2 - x
LK
Những câu hỏi liên quan
BT6: Thu gọn về hàng đẳng thức5,left(x-yright)^2+left(x+yright)^2-2left(x+yright)left(x-yright)6,left(5-xright)^2+left(x+5right)^2-left(2x+10right)left(x-5right)7,left(x-2right)^2+left(x+1right)^2+2left(x-2right)left(-1-xright)8,-left(2x+3yright)^2+left(2x-3yright)^2-2left(4x^2-9y^2right)
Đọc tiếp
BT6: Thu gọn về hàng đẳng thức
\(5,\left(x-y\right)^2+\left(x+y\right)^2-2\left(x+y\right)\left(x-y\right)\)
\(6,\left(5-x\right)^2+\left(x+5\right)^2-\left(2x+10\right)\left(x-5\right)\)
\(7,\left(x-2\right)^2+\left(x+1\right)^2+2\left(x-2\right)\left(-1-x\right)\)
\(8,-\left(2x+3y\right)^2+\left(2x-3y\right)^2-2\left(4x^2-9y^2\right)\)
5) \(\left(x-y\right)^2+\left(x+y\right)^2-2\left(x+y\right)\left(x-y\right)\)
\(=\left(x-y\right)^2-2\left(x-y\right)\left(x+y\right)+\left(x+y\right)^2\)
\(=\left[\left(x-y\right)-\left(x+y\right)\right]^2\)
\(=\left(x-y-x-y\right)^2\)
\(=\left(-2y^2\right)\)
\(=4y^2\)
6) \(\left(5-x\right)^2+\left(x+5\right)^2-\left(2x+10\right)\left(x-5\right)\)
\(=\left(x-5\right)^2-2\left(x-5\right)\left(x+5\right)+\left(x+5\right)^2\)
\(=\left[\left(x-5\right)-\left(x+5\right)\right]^2\)
\(=\left(x-5-x-5\right)^2\)
\(=\left(-10\right)^2=100\)
7) \(\left(x-2\right)^2+\left(x+1\right)^2+2\left(x-2\right)\left(-1-x\right)\)
\(=\left(x-2\right)^2-2\left(x-2\right)\left(x+1\right)+\left(x+1\right)^2\)
\(=\left[\left(x-2\right)-\left(x+1\right)\right]^2\)
\(=\left(-3\right)^2=9\)
8) \(-\left(2x+3y\right)^2+\left(2x-3y\right)^2-2\left(4x^2-9y^2\right)\)
\(=\left(2x-3y\right)^2+2\left(2x+3y\right)\left(2x-3y\right)+\left(2x+3y\right)^2\)
\(=\left[\left(2x+3y\right)+\left(2x-3y\right)\right]^2\)
\(=\left(4x\right)^2=16x^2\)
Đúng 1
Bình luận (0)
Pleft(frac{sqrt{x}-2}{x-1}-frac{sqrt{x}+2}{x+2sqrt{x}+1}right)frac{left(1-xright)^2}{2}Pleft(frac{sqrt{x}-2}{left(sqrt{x}-1right)left(sqrt{x}+1right)}-frac{sqrt{x}+2}{left(sqrt{x}+1right)^2}right)frac{left(1-xright)^2}{2}Pleft(frac{left(sqrt{x}-2right)left(sqrt{x}+1right)-left(sqrt{x}+2right)left(sqrt{x}-1right)}{left(x-1right)left(sqrt{x}+1right)}right)frac{left(x-1right)^2}{2}Pleft(frac{left(x-sqrt{x}-2right)-left(x+sqrt{x}-2right)}{left(x-1right)left(sqrt{x}+1right)}right)frac{left(x-1right)^...
Đọc tiếp
\(P=\left(\frac{\sqrt{x}-2}{x-1}-\frac{\sqrt{x}+2}{x+2\sqrt{x}+1}\right)\frac{\left(1-x\right)^2}{2}\)
\(P=\left(\frac{\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\frac{\sqrt{x}+2}{\left(\sqrt{x}+1\right)^2}\right)\frac{\left(1-x\right)^2}{2}\)
\(P=\left(\frac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)-\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\left(x-1\right)\left(\sqrt{x}+1\right)}\right)\frac{\left(x-1\right)^2}{2}\)
\(P=\left(\frac{\left(x-\sqrt{x}-2\right)-\left(x+\sqrt{x}-2\right)}{\left(x-1\right)\left(\sqrt{x}+1\right)}\right)\frac{\left(x-1\right)^2}{2}\)
\(P=\frac{2\sqrt{x}}{\left(x-1\right)\left(\sqrt{x}+1\right)}\frac{\left(x-1\right)^2}{2}\)
\(P=\frac{\sqrt{x}\left(x-1\right)}{\sqrt{x}+1}=\sqrt{x}\left(\sqrt{x}-1\right)=x-\sqrt{x}\)
1) Đa thứcleft(x^2+x+1right)left(X^2+x+2right)-12 được phân tích thành nhân tử là:A)left(x^2+x+5right)left(x+2right)left(x-1right)B)left(x^2+x-5right)left(x+2right)left(x-1right)C)left(x^2-x+5right)left(x+2right)left(x-1right)D)left(x^2+x+5right)left(x-2right)left(x+1right)2) left(x+aright)left(x+2aright)left(x+3aright)left(x+4aright)+a^4 được phân tích thành nhân tử là:A)left(x^2+5ax-5a^2right)left(x^2-5ax+5a^2right)B)left(x^2-5ax-5a^2right)left(x^2+5ax+5a^2right)C)left(x^2-5ax-5a^2right)left(x...
Đọc tiếp
1) Đa thức\(\left(x^2+x+1\right)\left(X^2+x+2\right)\)-12 được phân tích thành nhân tử là:
A)\(\left(x^2+x+5\right)\left(x+2\right)\left(x-1\right)\)
B)\(\left(x^2+x-5\right)\left(x+2\right)\left(x-1\right)\)
C)\(\left(x^2-x+5\right)\left(x+2\right)\left(x-1\right)\)
D)\(\left(x^2+x+5\right)\left(x-2\right)\left(x+1\right)\)
2) \(\left(x+a\right)\left(x+2a\right)\left(x+3a\right)\left(x+4a\right)+a^4\) được phân tích thành nhân tử là:
A)\(\left(x^2+5ax-5a^2\right)\left(x^2-5ax+5a^2\right)\)
B)\(\left(x^2-5ax-5a^2\right)\left(x^2+5ax+5a^2\right)\)
C)\(\left(x^2-5ax-5a^2\right)\left(x^2-5ax+5a^2\right)\)
D)\(\left(x^2+5ax+5a^2\right)^{^2}\)
3) Đa thức \(a^3+b^3+c^3-3abc\) được phân tích thành nhân tử là:
A)\(\left(a+b+c\right)\left(a^2+b^2+c^2-ab+bc-ca\right)\)
B)\(\left(a-b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)\)
C)\(\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)\)
D)\(\left(a+b+c\right)\left(a^2+b^2+c^2-ab+bc-ca\right)\)
4) Đa thức x(x+1)(x+2)(x+3)+1 được phân tích thành nhân tử là:
A)\(\left(x^2+3x+1\right)\left(x^2+3x-1\right)\)
B)\(\left(x^2+3x+1\right)^{^2}\)
C)\(\left(x^2+3x+1\right)\left(x^2-3x+1\right)\)
D) Cả B và C đều sai
5) Câu trả lời đúng cho M=\(n^2\left(n+1\right)+2n\left(n+1\right)+360\) với \(n\in Z\)
A)M⋮4
B)M⋮5
C)M⋮6
D)M⋮9
6)Cho \(P=\left(2n+5\right)^{^2}-145\) với \(n\in N\)
A) P⋮4 ; B)P⋮3 ; C) P⋮5 ; D)P⋮6
7) Giá trị của biểu thức \(x^2-y^2-2y-1\) tại
x=502 ; y=497 là:
A) 3000
B)5000
C)4500
D) cả A và B đều sai
Bạn nên tách bài ra để đăng. Không nên đăng 1 loạt như thế này.
Đúng 0
Bình luận (0)
1) Đa thứcleft(x^2+x+1right)left(X^2+x+2right)-12 được phân tích thành nhân tử là:A)left(x^2+x+5right)left(x+2right)left(x-1right)B)left(x^2+x-5right)left(x+2right)left(x-1right)C)left(x^2-x+5right)left(x+2right)left(x-1right)D)left(x^2+x+5right)left(x-2right)left(x+1right) 2) left(x+aright)left(x+2aright)left(x+3aright)left(x+4aright)+a^4 được phân tích thành nhân tử là:A)left(x^2+5ax-5a^2right)left(x^2-5ax+5a^2right)B)left(x^2-5ax-5a^2right)left(x^2+5ax+5a^2right)C)left(x^2-5ax-5a^2right)left(...
Đọc tiếp
1) Đa thức\(\left(x^2+x+1\right)\left(X^2+x+2\right)\)-12 được phân tích thành nhân tử là:
A)\(\left(x^2+x+5\right)\left(x+2\right)\left(x-1\right)\)
B)\(\left(x^2+x-5\right)\left(x+2\right)\left(x-1\right)\)
C)\(\left(x^2-x+5\right)\left(x+2\right)\left(x-1\right)\)
D)\(\left(x^2+x+5\right)\left(x-2\right)\left(x+1\right)\)
2) \(\left(x+a\right)\left(x+2a\right)\left(x+3a\right)\left(x+4a\right)+a^4\) được phân tích thành nhân tử là:
A)\(\left(x^2+5ax-5a^2\right)\left(x^2-5ax+5a^2\right)\)
B)\(\left(x^2-5ax-5a^2\right)\left(x^2+5ax+5a^2\right)\)
C)\(\left(x^2-5ax-5a^2\right)\left(x^2-5ax+5a^2\right)\)
D)\(\left(x^2+5ax+5a^2\right)^{^2}\)
3) Đa thức \(a^3+b^3+c^3-3abc\) được phân tích thành nhân tử là:
A)\(\left(a+b+c\right)\left(a^2+b^2+c^2-ab+bc-ca\right)\)
B)\(\left(a-b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)\)
C)\(\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)\)
D)\(\left(a+b+c\right)\left(a^2+b^2+c^2-ab+bc-ca\right)\)
5) Câu trả lời đúng cho M=\(n^2\left(n+1\right)+2n\left(n+1\right)+360\) với \(n\in Z\)
A)M⋮4
B)M⋮5
C)M⋮6
D)M⋮9
6)Cho \(P=\left(2n+5\right)^{^2}-145\) với \(n\in N\)
A) P⋮4 ; B)P⋮3 ; C) P⋮5 ; D)P⋮6
7) Giá trị của biểu thức \(x^2-y^2-2y-1\) tại
x=502 ; y=497 là:
A) 3000
B)5000
C)4500
D) cả A và B đều sai
1: \(=\left(x^2+x\right)^2+3\left(x^2+x\right)+2-12\)
=(x^2+x)^2+3(x^2+x)-10
=(x^2+x+5)(x^2+x-2)
=(x^2+x+5)(x+2)(x-1)
2: \(=\left(x^2+5ax+4a^2\right)\left(x^2+5ax+6a^2\right)+a^4\)
\(=\left(x^2+5ax\right)^2+10a^2\left(x^2+5ax\right)+25a^2\)
\(=\left(x^2+5ax+5a^2\right)^2\)
3: \(=\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc\)
\(=\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2\right)-3ab\left(a+b+c\right)\)
\(=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-ac-bc\right)\)
5: \(M=\left(n+1\right)\left(n^2+2n\right)+360\)
=n(n+1)(n+2)+360 chia hết cho 6
6A
7D
Đúng 1
Bình luận (0)
Tìm x biết :a) left(x-2right)^3+6left(x+1right)^2-x^3+120b) left(x-5right)left(x+5right)-left(x+3right)^3+3left(x-2right)^2left(x+1right)^2-left(x+4right)left(x-4right)+3x^2c) left(2x+3right)^2+left(x-1right)left(x+1right)5left(x+2right)^2-left(x-5right)left(x+1right)+left(x+4right)^2d) left(1-3xright)^2-left(x-2right)left(9x+1right)left(3x-4right)left(3x+4right)-9left(x+3right)^2
Đọc tiếp
Tìm x biết :
a) \(\left(x-2\right)^3+6\left(x+1\right)^2-x^3+12=0\)
b) \(\left(x-5\right)\left(x+5\right)-\left(x+3\right)^3+3\left(x-2\right)^2=\left(x+1\right)^2-\left(x+4\right)\left(x-4\right)+3x^2\)
c) \(\left(2x+3\right)^2+\left(x-1\right)\left(x+1\right)=5\left(x+2\right)^2-\left(x-5\right)\left(x+1\right)+\left(x+4\right)^2\)
d) \(\left(1-3x\right)^2-\left(x-2\right)\left(9x+1\right)=\left(3x-4\right)\left(3x+4\right)-9\left(x+3\right)^2\)
a/ \(x=\dfrac{-5}{12}\)
b/ \(x\approx-1,9526\)
c/ \(x=\dfrac{21-i\sqrt{199}}{10}\)
d/ \(x=\dfrac{-20}{13}\)
Đúng 0
Bình luận (0)
a) (x-2)3+6(x+1)2-x3+12=0
⇒ x3-6x2+12x-8+6(x2+2x+1)-x3+12=0
⇒ x3-6x2+12x-8+6x2+12x+6-x3+12=0
⇒ 24x+10=0
⇒ 24x=-10
⇒ x=-5/12
Đúng 0
Bình luận (0)
a.
PT \(\Leftrightarrow x^3-6x^2+12x-8+6(x^2+2x+1)-x^3+12=0\)
\(\Leftrightarrow x^3-6x^2+12x-8+6x^2+12x+6-x^3+12=0\)
\(\Leftrightarrow 24x+10=0\Leftrightarrow x=\frac{-5}{12}\)
b. Bạn xem lại đề, nghiệm khá xấu không phù hợp với mức độ tổng thể của bài.
c.
PT $\Leftrightarrow (4x^2+12x+9)+(x^2-1)=5(x^2+4x+4)+(x^2-4x-5)+9(x^2+6x+9)$
$\Leftrightarrow 10x^2+42x+64=0$
$\Leftrightarrow x^2+(3x+7)^2=-15< 0$ (vô lý)
Do đó pt vô nghiệm.
d.
PT $\Leftrightarrow (1-6x+9x^2)-(9x^2-17x-2)=(9x^2-16)-9(x^2+6x+9)$
$\Leftrightarrow 11x+3=-54x-97$
$\Leftrightarrow 65x=-100$
$\Leftrightarrow x=\frac{-20}{13}$
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Giải phương trình:
\(8\left(x+\frac{1}{x}\right)^2+4\left(x^2+\frac{1}{^{x^2}}\right)^2-4\left(x^2+\frac{1}{x^2}\right)\left(x+\frac{1}{x}\right)^2=\left(x+4\right)^2\)
\(\frac{\left(2009-x\right)^2+\left(2009-x\right)\left(x-2010\right)+\left(x-2010\right)^2}{\left(2009-x\right)^2-\left(2009-x\right)\left(x-2010\right)+\left(x-2010\right)^2}=\frac{19}{49}\)
giải phương trình1)2left(x-3right)+12left(x+1right)-92)dfrac{5-x}{2}dfrac{3x-4}{6}3) left(x-1right)^2+left(x+2right)left(x-2right)left(2x+1right)left(x-3right)4)left(x+5right)left(x-1right)-left(x+1right)left(x+2right)15) dfrac{6x-1}{15}-dfrac{x}{5}dfrac{2x}{3}6)dfrac{5left(x-2right)}{2}-dfrac{x+5}{3}1-dfrac{4left(x-3right)}{5}
Đọc tiếp
giải phương trình
1)\(2\left(x-3\right)+1=2\left(x+1\right)-9\)
2)\(\dfrac{5-x}{2}=\dfrac{3x-4}{6}\)
3) \(\left(x-1\right)^2+\left(x+2\right)\left(x-2\right)=\left(2x+1\right)\left(x-3\right)\)
4)\(\left(x+5\right)\left(x-1\right)-\left(x+1\right)\left(x+2\right)=1\)
5) \(\dfrac{6x-1}{15}-\dfrac{x}{5}=\dfrac{2x}{3}\)
6)\(\dfrac{5\left(x-2\right)}{2}-\dfrac{x+5}{3}=1-\dfrac{4\left(x-3\right)}{5}\)
\(1,2\left(x-3\right)+1=2\left(x+1\right)-9\\ \Rightarrow2x-6+1=2x+2-9\\ \Rightarrow2x-5=2x-7\\ \Rightarrow-2=0\left(vô.lí\right)\)
\(2,\dfrac{5-x}{2}=\dfrac{3x-4}{6}\\ \Rightarrow30-6x=6x-8\\ \Rightarrow12x=38\\ \Rightarrow x=\dfrac{19}{6}\)
\(3,\left(x-1\right)^2+\left(x+2\right)\left(x-2\right)=\left(2x+1\right)\left(x-3\right)\\ \Rightarrow x^2-2x+1+x^2-4=2x^2-6x+x-3\\ \Rightarrow2x^2-2x-3=2x^2-5x-3\\ \Rightarrow3x=0\\ \Rightarrow x=0\)
\(4,\left(x+5\right)\left(x-1\right)-\left(x+1\right)\left(x+2\right)=1\\ \Rightarrow x^2+5x-x-5-x^2-2x-x-2=1\\ \\ \Rightarrow x-7=1\\ \Rightarrow x=8\)
Đúng 1
Bình luận (0)
\(5,\dfrac{6x-1}{15}-\dfrac{x}{5}=\dfrac{2x}{3}\\ \Rightarrow\dfrac{6x-1}{15}-\dfrac{3x}{15}=\dfrac{10x}{15}\\ \Rightarrow6x-1-3x=10x\\ \Rightarrow3x-1=10x\\ \Rightarrow7x=-1\\ \Rightarrow x=\dfrac{-1}{7}\)
\(6,\dfrac{5\left(x-2\right)}{2}-\dfrac{x+5}{3}=1-\dfrac{4\left(x-3\right)}{5}\\ \Rightarrow\dfrac{75\left(x-2\right)}{30}-\dfrac{10\left(x+5\right)}{30}=\dfrac{30}{30}-\dfrac{24\left(x-3\right)}{30}\\ \Rightarrow75\left(x-2\right)-10\left(x+5\right)=30-24\left(x-3\right)\\ \Rightarrow75x-150-10x-50=30-24x+72\\ \Rightarrow65x-200=102-24x\\ \Rightarrow89x=302\\ \Rightarrow x=\dfrac{320}{89}\)
Đúng 0
Bình luận (0)
left(x^2-x+1right)^4-6x^2left(x^2-x+1right)^2+5x^40
Leftrightarrowleft[left(x^2-x+1right)^2right]^2-2left(x^2-x+1right)^2.3x^2+left(3x^2right)^2-4x^40
Leftrightarrowleft[left(x^2-x+1right)^2-3x^2right]^2-left(2x^2right)^20
Leftrightarrowleft[left(x^2-x+1right)^2-3x^2+2x^2right]left[left(x^2-x+1right)^2-3x^2-2x^2right]0
Leftrightarrowleft[left(x^2-x+1right)^2-x^2right]left[left(x^2-x+1right)^2-5x^2right]0
Leftrightarrowleft(x^2-x+1+x^2right)left(x^2-x+1-x^2right)left(x^4-2x^3-4x^2+1right)0...
Đọc tiếp
\(\left(x^2-x+1\right)^4-6x^2\left(x^2-x+1\right)^2+5x^4=0\)
\(\Leftrightarrow\left[\left(x^2-x+1\right)^2\right]^2-2\left(x^2-x+1\right)^2.3x^2+\left(3x^2\right)^2-4x^4=0\)
\(\Leftrightarrow\left[\left(x^2-x+1\right)^2-3x^2\right]^2-\left(2x^2\right)^2=0\)
\(\Leftrightarrow\left[\left(x^2-x+1\right)^2-3x^2+2x^2\right]\left[\left(x^2-x+1\right)^2-3x^2-2x^2\right]=0\)
\(\Leftrightarrow\left[\left(x^2-x+1\right)^2-x^2\right]\left[\left(x^2-x+1\right)^2-5x^2\right]=0\)
\(\Leftrightarrow\left(x^2-x+1+x^2\right)\left(x^2-x+1-x^2\right)\left(x^4-2x^3-4x^2+1\right)=0\)
\(\Leftrightarrow\left(2x^2-x+1\right)\left(1-x\right)\left(x+1\right)\left(x^3-2x^2-x+1\right)=0\)
Mấy bạn cho mình gửi tạm nha, xíu mình nhờ CTV xóa :(
i, \(\left(x-1\right)\left(x+3\right)-\left(x-1\right)\left(2x+1\right)=0\)
k, \(\left(x+2\right)\left(x+1\right)-\left(x-3\right)\left(x+2\right)=0\)
l, \(\left(x-2\right)\left(x+3\right)=\left(x-2\right)\left(2x+5\right)\)
\(\left(x-1\right)\left(-x+2\right)=0\Leftrightarrow x=1;x=2\)
\(\left(x+2\right)\left(x+1-x+3\right)=0\Leftrightarrow x=-2\)
\(\left(x-2\right)\left(x+3\right)-\left(x-2\right)\left(2x+5\right)=0\Leftrightarrow\left(x-2\right)\left(-x-2\right)=0\Leftrightarrow x=-2;x=2\)
Đúng 4
Bình luận (0)
\(i,\left(x-1\right)\left(x+3\right)-\left(x-1\right)\left(2x+1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x+3-2x-1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(-x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\\ k,\left(x+2\right)\left(x+1\right)-\left(x-3\right)\left(x+2\right)=0\\ \Leftrightarrow\left(x+2\right)\left(x+1-x+3\right)=0\\ \Leftrightarrow4\left(x+2\right)=0\\ \Leftrightarrow x+2=0\\ \Leftrightarrow x=-2\\ l,\left(x-2\right)\left(x+3\right)=\left(x-2\right)\left(2x+5\right)\\ \Leftrightarrow\left(x-2\right)\left(2x+5\right)-\left(x-2\right)\left(x+3\right)=0\\ \Leftrightarrow\left(x-2\right)\left(2x+5-x-3\right)=0\\ \Leftrightarrow\left(x-2\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)
Đúng 2
Bình luận (0)
left(frac{1}{2+2sqrt{x}}+frac{1}{2-2sqrt{x}}-frac{x^2+1}{1-x^2}right)left(1+frac{1}{x}right)left(frac{2-2sqrt{x}+2+2sqrt{x}}{left(2+2sqrt{x}right)left(2-2sqrt{x}right)}-frac{x^2+1}{1-x^2}right)left(1+frac{1}{x}right)left(frac{4}{4-4x}-frac{x^2+1}{left(1-xright)left(1+xright)}right)left(1+frac{1}{x}right)left(frac{1+x-x^2-1}{left(1-xright)left(1+xright)}right)left(1+frac{1}{x}right)frac{xleft(1-xright)}{left(1-xright)left(1+xright)}.frac{x+1}{x}1
Đọc tiếp
\(\left(\frac{1}{2+2\sqrt{x}}+\frac{1}{2-2\sqrt{x}}-\frac{x^2+1}{1-x^2}\right)\left(1+\frac{1}{x}\right)\)
\(=\left(\frac{2-2\sqrt{x}+2+2\sqrt{x}}{\left(2+2\sqrt{x}\right)\left(2-2\sqrt{x}\right)}-\frac{x^2+1}{1-x^2}\right)\left(1+\frac{1}{x}\right)\)
\(=\left(\frac{4}{4-4x}-\frac{x^2+1}{\left(1-x\right)\left(1+x\right)}\right)\left(1+\frac{1}{x}\right)\)
\(=\left(\frac{1+x-x^2-1}{\left(1-x\right)\left(1+x\right)}\right)\left(1+\frac{1}{x}\right)=\frac{x\left(1-x\right)}{\left(1-x\right)\left(1+x\right)}.\frac{x+1}{x}=1\)
Nếu bạn bảo kiểm tra thì lời giải đúng rồi nhé!
Đúng 0
Bình luận (0)