Tìm m để hàm số y= (3m-2)x2+4 nghịch biến trên (-vô cực; 0)
LN
Những câu hỏi liên quan
a/ cho hàm số: y=(-3m - 2)x2. Tìm m để hàm số nghịch biến khi x < 0
b/ cho hàm số: y=(m2 - 2m + 3)x2. Xác định tính biến thiên của hàm số
c/ cho hàm số: y=(2m + 3)x2. Tìm m để hàm số đồng biến khi x>0
a.
Hàm số nghịch biến khi \(x< 0\Rightarrow-3m-2>0\Rightarrow m< -\dfrac{2}{3}\)
b.
Do \(a=m^2-2m+3=\left(m-1\right)^2+2>0;\forall m\)
\(\Rightarrow\) Hàm đồng biến khi \(x>0\) và nghịch biến khi \(x< 0\)
c.
Hàm đồng biến khi \(x>0\Rightarrow2m+3>0\)
\(\Rightarrow m>-\dfrac{3}{2}\)
Đúng 1
Bình luận (0)
cho hàm số y=f(x)=-x^2-2x+1. Mệnh đề nào sau đây là đúng? A. Hàm số nghịch biến trên khoảng (-1;+vô cực) B. Hàm số nghịch biến trên khoảng (-vô cực;-1) C. Hàm số đồng biến trên khoảng (-1;+vô cực) D. Hàm số đồng biến trên khoảng (-vô cực;0)
B. Hàm số nghịch biến trên khoảng \(\left(-\infty;-1\right)\)
Đúng 3
Bình luận (0)
Tìm m để hàm số y = - 2x^2- (2m - 1)x + 6 - 3m nghịch biến trong khoảng (-2 ; dương vô cùng)
Xét parabol \(\left(C_m\right):y=-2x^2-\left(2m-1\right)x+6-3m\), ta có \(\Delta=\left[-\left(2m-1\right)\right]^2-4\left(-2\right)\left(6+3m\right)=4m^2+20m+49\)
Gọi \(I_m\) là đỉnh của \(\left(C_m\right)\) thì \(I_m\left(\dfrac{-2m+1}{4};\dfrac{4m^2+20m+49}{8}\right)\)
Để hàm số đã cho nghịch biến trong khoảng \(\left(-2;+\infty\right)\) thì \(\dfrac{-2m+1}{4}=-2\Leftrightarrow m=\dfrac{9}{2}\)
Đúng 1
Bình luận (0)
Tao đéo biết thằng Nguyễn Huy Hung nha ☹
Đúng 0
Bình luận (0)
Để hàm số nghịch biến trên \(\left(-2;+\infty\right)\)
\(\Rightarrow\left(-2;+\infty\right)\subset\left(\dfrac{1-2m}{4};+\infty\right)\)
\(\Rightarrow\dfrac{1-2m}{4}\ge-2\)
\(\Rightarrow m\le\dfrac{9}{2}\)
Đúng 0
Bình luận (0)
cho y=1/3x³-(m-2)x²+(m²-3m+2)x+3. tìm m để a)Hàm số đồng biến với mọi x thuộc (2;dương vô cùng) b)Hàm số đồng biến với mọi x thuộc (trừ âm vô cùng;0) c)Hàm số nghịch biến với mọi x thuộc (-2;3)
\(y'=x^2-2\left(m-2\right)x+m^2-3m+2\)
a. Hàm đồng biến trên khoảng đã cho khi và chỉ khi:
\(y'\ge0\) ; \(\forall x>3\)
\(\Leftrightarrow x^2-2\left(m-2\right)x+m^2-3m+2\ge0\) ; \(\forall x>3\)
Ta có: \(\Delta'=\left(m-2\right)^2-\left(m^2-3m+2\right)=-m+2\)
TH1: \(\Delta'\le0\Leftrightarrow m\ge2\)
TH2: \(\left\{{}\begin{matrix}\Delta'>0\\x_1< x_2\le2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m< 2\\\left(x_1-2\right)\left(x_2-2\right)\ge0\\\dfrac{x_1+x_2}{2}< 2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 2\\x_1x_2-2\left(x_1+x_2\right)+4\ge0\\x_1+x_2< 4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 2\\m^2-3m+2-4\left(m-2\right)+4\ge0\\2\left(m-2\right)< 4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 2\\m^2-7m+4\ge0\\m< 4\end{matrix}\right.\) \(\Leftrightarrow m< 2\)
Kết hợp lại ta được hàm đồng biến trên \(\left(2;+\infty\right)\) với mọi m
Đúng 3
Bình luận (0)
b.
Hàm số đồng biến trên khoảng đã cho khi và chỉ khi:
\(y'\ge0\) ; \(\forall x< 0\)
\(\Leftrightarrow x^2-2\left(m-2\right)x+m^2-3m+2\ge0\) ; \(\forall x< 0\)
TH1: \(\Delta'=-m+2\le0\Leftrightarrow m\ge2\)
TH2: \(\left\{{}\begin{matrix}\Delta'>0\\0\le x_1< x_2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 2\\x_1+x_2=2\left(m-2\right)>0\\x_1x_2=m^2-3m+2\ge0\end{matrix}\right.\) \(\Rightarrow\) ko tồn tại m thỏa mãn
Kết hợp lại ta được: \(m\ge2\)
Đúng 2
Bình luận (0)
c.
Hàm số nghịch biến trên khoảng đã cho khi và chỉ khi:
\(f\left(x\right)=x^2-2\left(m-2\right)x+m^2-4m+3\le0\) ; \(\forall x\in\left(-2;3\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'>0\\x_1\le-2< 3\le x_2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 2\\f\left(-2\right)\le0\\f\left(3\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 2\\4+4\left(m-2\right)+m^2-4m+3\le0\\9-6\left(m-2\right)+m^2-4m+3\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 2\\m^2\le1\\m^2-10m+24\le0\end{matrix}\right.\) \(\Rightarrow\) không tồn tại m thỏa mãn
Đúng 2
Bình luận (0)
Bài 3: Cho hàm số: y left(m^2-4right).x + 3m - 1 (m ne pm 2)
a) Tìm m để hàm số đồng biến
b) Tìm m để hàm số nghịch biến
Đọc tiếp
Bài 3: Cho hàm số: y = \(\left(m^2-4\right)\).x + 3m - 1 (m \(\ne\) \(\pm\) 2)
a) Tìm m để hàm số đồng biến
b) Tìm m để hàm số nghịch biến
Tìm `m` để hàm số \(y=\dfrac{m^2}{3-4m}x+3m-2\) nghịch biến trên `R`.
Để đây là hàm số bậc nhất thì \(\dfrac{m^2}{3-4m}< >0\)
=>\(m\notin\left\{0;\dfrac{3}{4}\right\}\)
Để hàm số \(y=\dfrac{m^2}{3-4m}x+3m-2\) nghịch biến trên R thì
\(\dfrac{m^2}{3-4m}< 0\)
=>3-4m<0
=>-4m<-3
=>\(m>\dfrac{3}{4}\)
Đúng 1
Bình luận (0)
Tìm m để hàm số
y
x
-
3
m
-
x
nghịch biến trên (0;1).
Đọc tiếp
Tìm m để hàm số y = x - 3 m - x nghịch biến trên (0;1).
![]()
![]()
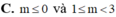
![]()
tìm m để hàm số \(y=\dfrac{x^3}{3}-\dfrac{mx^2}{2}+2mx-3m+4\) nghịch biến trên một đoạn có độ dài bằng 3.
\(y'=x^2-mx+2m\)
Hàm nghịch biến trên 1 đoạn có độ dài 3 khi và chỉ khi \(y'=0\) có 2 nghiệm pb thỏa mãn:
\(\left|x_1-x_2\right|=3\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta=m^2-8m>0\\\left(x_1+x_2\right)^2-4x_1x_2=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m< 0\\m>8\end{matrix}\right.\\m^2-8m=9\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}m=-1\\m=9\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Bài 3: Cho hàm số: y = \(\left(m^2-4\right)\).x + 3m - 1 (m \(\ne\) \(\pm\) 2)
a) Tìm m để hàm số đồng biến
b) Tìm m để hàm số nghịch biến
a: Để hàm số đồng biến trên R thì \(m^2-4>0\)
=>\(m^2>4\)
=>\(\left[{}\begin{matrix}m>2\\m< -2\end{matrix}\right.\)
b: Để hàm số nghịch biến trên R thì \(m^2-4< 0\)
=>\(m^2< 4\)
=>-2<m<2
Đúng 0
Bình luận (0)
a) Hàm số y = (3m - 1)x + 2 với m ≠≠ 1313
Vậy m > 1313 nghịch biến
⇔ 3m - 1 < 0
⇔ 3m < 1
⇔ m < 1313 thì hàm số y = (3m - 1)x + 2 nghịch biến
c) Đồ thị hàm số y = (3m - 1)x + 2 với m ≠≠ 1313)
⇔ 3 = 6m - 2 + 2
⇔ 3 = 6m
⇔ m = 1212 thì đồ thị hàm số y = (3m - 1)x + 2 đi qua điểm A(2; 3)
Đúng 0
Bình luận (0)
a) Hàm số đồng biến khi:
m² - 4 > 0
⇔ m² > 4
⇔ m < -2 hoặc m > 2
Vậy m < -2; m > 2 thì hàm số đồng biến
b) Hàm số nghịch biến khi:
m² - 4 < 0
⇔ m² < 4
⇔ -2 < m < 2
Vậy -2 < m < 2 thì hàm số nghịch biến
Đúng 0
Bình luận (0)
có bao nhiêu giá trị nguyên của tham số M để hàm số y= x+1/ x+3M nghịch biến trên khoảng (6;+∞)
A 0 B6 C3 D vô số







