Giải PT: tanx= cotx+4cos2x
LH
Những câu hỏi liên quan
giải pt \(tanx-cotx=\frac{3}{2}\)
ĐKXĐ: ...
\(tanx-\frac{1}{tanx}=\frac{3}{2}\)
\(\Leftrightarrow tan^2x-\frac{3}{2}tanx-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=2\\tanx=-\frac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow...\)
Giải pt sau:
\(2\left(Tan^2x-Cot^2x\right)-5\left(Tanx+Cotx\right)+6=0\)
giải pt: /tanx/=cotx+\(\frac{1}{c\text{os}x}\)
Giải pt
\(cotx-tanx=sinx+cosx\)
\(sinx+cosx+\dfrac{1}{sinx}+\dfrac{1}{cosx}=\dfrac{10}{3}\)
1.
ĐK: \(x\ne\dfrac{k\pi}{2}\)
\(cotx-tanx=sinx+cosx\)
\(\Leftrightarrow\dfrac{cosx}{sinx}-\dfrac{sinx}{cosx}=sinx+cosx\)
\(\Leftrightarrow\dfrac{cos^2x-sin^2x}{sinx.cosx}=sinx+cosx\)
\(\Leftrightarrow\left(\dfrac{cosx-sinx}{sinx.cosx}-1\right)\left(sinx+cosx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx+cosx=0\left(1\right)\\cosx-sinx=sinx.cosx\left(2\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=0\Leftrightarrow x=-\dfrac{\pi}{4}+k\pi\)
\(\left(2\right)\Leftrightarrow t=\dfrac{1-t^2}{2}\left(t=cosx-sinx,\left|t\right|\le2\right)\)
\(\Leftrightarrow t^2+2t-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=-1+\sqrt{2}\\t=-1-\sqrt{2}\left(l\right)\end{matrix}\right.\)
\(\Leftrightarrow cosx-sinx=-1+\sqrt{2}\)
\(\Leftrightarrow-\sqrt{2}sin\left(x-\dfrac{\pi}{4}\right)=-1+\sqrt{2}\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}-1}{\sqrt{2}}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+arcsin\left(\dfrac{\sqrt{2}-1}{\sqrt{2}}\right)+k2\pi\\x=\dfrac{5\pi}{4}-arcsin\left(\dfrac{\sqrt{2}-1}{\sqrt{2}}\right)+k2\pi\end{matrix}\right.\)
Vậy phương trình đã cho có nghiệm:
\(x=-\dfrac{\pi}{4}+k\pi;x=\dfrac{\pi}{4}+arcsin\left(\dfrac{\sqrt{2}-1}{\sqrt{2}}\right)+k2\pi;x=\dfrac{5\pi}{4}-arcsin\left(\dfrac{\sqrt{2}-1}{\sqrt{2}}\right)+k2\pi\)
Đúng 0
Bình luận (0)
giải pt :
\(sinx+cosx=\frac{2}{tanx}-\frac{2}{cotx}\)
ĐKXĐ: \(sin2x\ne0\Leftrightarrow x\ne\frac{k\pi}{2}\)
\(sinx+cosx=\frac{2cosx}{sinx}-\frac{2sinx}{cosx}\)
\(\Leftrightarrow sinx+cosx=\frac{2\left(cos^2x-sin^2x\right)}{sinx.cosx}\)
\(\Leftrightarrow sinx+cosx=\frac{2\left(sinx+cosx\right)\left(cosx-sinx\right)}{sinx.cosx}\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx+cosx=0\Leftrightarrow sin\left(x+\frac{\pi}{4}\right)=0\Leftrightarrow...\\\frac{2\left(cosx-sinx\right)}{sinx.cosx}=1\left(1\right)\end{matrix}\right.\)
Xét (1) \(\Leftrightarrow2\left(cosx-sinx\right)=sinx.cosx\)
Đặt \(cosx-sinx=t\Rightarrow\left\{{}\begin{matrix}\left|t\right|\le\sqrt{2}\\sinx.cosx=\frac{1-t^2}{2}\end{matrix}\right.\)
\(\Rightarrow2t=\frac{1-t^2}{2}\Leftrightarrow t^2-4t-1=0\)
\(\Rightarrow\left[{}\begin{matrix}t=2+\sqrt{5}\left(l\right)\\t=2-\sqrt{5}\end{matrix}\right.\)
\(\Rightarrow cosx-sinx=2-\sqrt{5}\)
\(\Leftrightarrow sin\left(x-\frac{\pi}{4}\right)=\frac{\sqrt{5}-2}{\sqrt{2}}=sina\)
\(\Rightarrow\left[{}\begin{matrix}x-\frac{\pi}{4}=a+k2\pi\\x-\frac{\pi}{4}=\pi-a+k2\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
3.tìm m để pt tanx(tanx-2)+cotx(cotx-2)=m
a. có nghiệm
b.có nghiệm thuộc (0;pi/4)
Đk : Cosx ≠ 0 và Sinx ≠ 0 ↔ x ≠ k. π/2. Khi đó :
<1> ↔ Tan^2x + cot^2x – 2( Tanx + cotx) = m
↔ [Tan^2x + 1/( Tan^2x)] – 2[ Tanx + 1/( Tanx)] = m
Đặt tanx + 1/tanx = t ( t € R )
PT trên trở thành
t^2 – 2 -2t = m<*>
a, Bài toán quy về tìm m để PT <*> có nghiệm
<*> ↔ t^2 – 2t -2 – m = 0
Để thỏa mãn thì ; ∆’ = 1 +2 + m ≥ 0 ↔ m ≥ - 3
b, Với x thuộc (0;pi/4) thì tanx > 0
Khi đó t ≥ 2 ( theo BĐT Cô-si)
Bài toán quy về tìm m để PT <*> có nghiệm t ≥ 2
Xét hàm số y = t^2 – 2t -2 trên [2; +∞)
Bạn cũng vẽ bảng biến thiên ra
Từ bảng biến thiên ta thấy để thỏa mãn thì
m ≥ -2
Đúng 0
Bình luận (0)
Giải phương trình : tanx + cotx=2
ĐKXĐ: \(x\ne k\dfrac{\pi}{2}\)
\(tanx+\dfrac{1}{tanx}=2\)
\(\Rightarrow tan^2x+1=2tanx\)
\(\Leftrightarrow\left(tanx-1\right)^2=0\)
\(\Leftrightarrow tanx=1\)
\(\Rightarrow x=\dfrac{\pi}{4}+k\pi\) (thỏa mãn)
Đúng 0
Bình luận (0)
Tìm GTLN, GTNN của hàm số y = √(1−2sinx)
Giải phương trình lượng giác
a) sin4x + cos4x + sin4x = 1
b) tan2x + cotx = 4cos2x
Giải phương trình cotx - tanx + 4sin2x = 2/sin2x
Đối với những phương trình lượng giác chứa tanx, cotx, sin2x hoặc cos2x, ta có thể đưa về phương trình chứa cosx, sinx, sin2x, hoặc cos2x ngoài ra cũng có thể đặt ẩn phụ t = tanx để đưa về một phương trình theo t.
Cách 1: Điều kiện của phương trình:
sin2x ≠ 0 ⇔ cos2x ≠ 1 hoặc cos2x ≠ -1 (1)
Ta có:
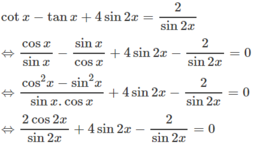
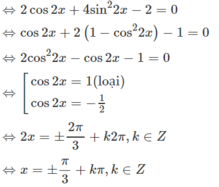
Cách 2. Đặt t = tanx
Điều kiện t ≠ 0
Phương trình đã cho có dạng
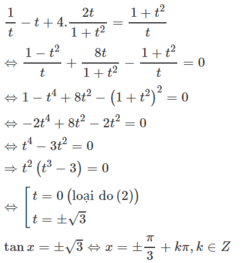
Đúng 0
Bình luận (0)


