Cần câu (c)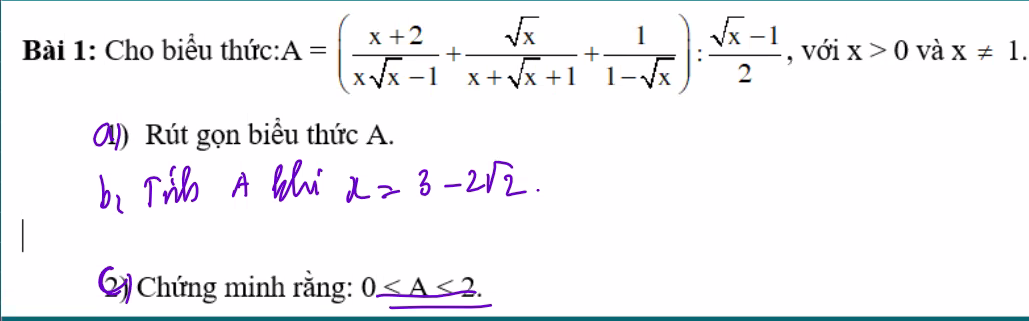
KG
Những câu hỏi liên quan
Câu a,b không cần làm ,chỉ cần làm câu c,d

Ko cần làm câu a đâu:3,mik cần câu b,c,d
Câu b bạn tự vẽ
Câu c:
PT hoành độ giao điểm: \(-3x+1=\left(1-2m\right)x+m-1\)
Mà 2 đt cắt tại hoành độ 1 nên \(x=1\)
\(\Leftrightarrow-2=1-2m+m-1\Leftrightarrow m=2\)
Câu d:
PT giao Ox,Oy lần lượt tại A,B của (d) là:
\(\left\{{}\begin{matrix}y=0\Rightarrow x=\dfrac{m-1}{2m-1}\Rightarrow A\left(\dfrac{m-1}{2m-1};0\right)\Rightarrow OA=\left|\dfrac{m-1}{2m-1}\right|\\x=0\Rightarrow y=m-1\Rightarrow B\left(0;m-1\right)\Rightarrow OB=\left|m-1\right|\end{matrix}\right.\)
Gọi H là chân đường cao từ O đến (d)
Đặt \(OH^2=t\)
Áp dụng HTL: \(\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}=\dfrac{\left(2m-1\right)^2}{\left(m-1\right)^2}+\dfrac{1}{\left(m-1\right)^2}\)
\(\Leftrightarrow\dfrac{1}{t}=\dfrac{4m^2-4m+2}{\left(m-1\right)^2}\Leftrightarrow t=\dfrac{m^2-2m+1}{4m^2-4m+2}\\ \Leftrightarrow4m^2t-4mt+2t=m^2-2m+1\\ \Leftrightarrow m^2\left(4t-1\right)+2m\left(1-2t\right)+2t-1=0\)
Coi đây là PT bậc 2 ẩn m, PT có nghiệm
\(\Leftrightarrow\Delta'=\left(1-2t\right)^2-\left(4t-1\right)\left(2t-1\right)\ge0\\ \Leftrightarrow4t^2-4t+1-8t^2+6t-1\ge0\\ \Leftrightarrow2t-4t^2\ge0\\ \Leftrightarrow2t\left(1-2t\right)\ge0\\ \Leftrightarrow0\le t\le\dfrac{1}{2}\)
\(\Leftrightarrow OH^2\le\dfrac{1}{2}\Leftrightarrow OH\le\dfrac{1}{\sqrt{2}}\)
Dấu \("="\Leftrightarrow\dfrac{m^2-2m+1}{4m^2-4m+2}=\dfrac{1}{2}\Leftrightarrow4m^2-4m+2=2m^2-4m+2\)
\(\Leftrightarrow2m^2=0\Leftrightarrow m=0\)
Vậy m=0 thỏa yêu cầu đề
Đúng 2
Bình luận (0)
GIÚP mình câu C vs ạ :((( mình cần câu C nhấtt
Giúp mình câu c với ạ, chỉ cần câu c thôi ạ!

Vì \(\widehat{MIA}=90^0\left(\text{góc nt chắn nửa đường tròn}\right)\) nên \(MI\perp IA\)
Xét \(\Delta MBP\) có \(\left\{{}\begin{matrix}PK\perp MB\left(PK\perp MN\right)\\MI\perp PB\left(MI\perp IA\right)\\\left\{H\right\}=PK\cap MI\end{matrix}\right.\) nên H là trực tâm
Do đó \(HB\perp PM\)
Mà \(AM\perp PM\Rightarrow HB\text{//}AM\)
Vì \(HB\text{//}OA\Rightarrow\dfrac{PB}{PA}=\dfrac{HB}{OA}\)
Ta có \(\sin MPB=\sin MPA=\dfrac{MA}{PA}=\dfrac{2OA}{PA}\)
\(\Rightarrow\dfrac{1}{2}BP\cdot\sin MPB=\dfrac{PB\cdot\dfrac{2OA}{PA}}{2}=\dfrac{PB\cdot2OA}{2PA}=\dfrac{PB}{PA}\cdot OA=\dfrac{HB}{OA}\cdot OA=HB\left(đpcm\right)\)
Đúng 1
Bình luận (0)
Mình đang cần câu b và câu c ạ
Tứ giác AOKC nội tiếp (K và A cùng nhìn OC dưới góc vuông)
\(\Rightarrow\widehat{ACO}=\widehat{AKO}\) (cùng chắn AO) (1)
Mà \(\widehat{ACO}=\widehat{IAO}\) (cùng phụ \(\widehat{AOC}\)) (2)
\(\widehat{IAO}=\widehat{OIA}\) (\(OI=OA\) nên tam giác OIA cân tại O) (3)
(1);(2);(3) \(\Rightarrow\widehat{OIA}=\widehat{AKO}\)
Do \(\widehat{OIA}\) và \(\widehat{AKO}\) cùng chắn OA \(\Rightarrow OKIA\) nội tiếp
c. Theo cmt \(\Rightarrow\widehat{AIK}+\widehat{AOK}=180^0\)
AOKC nội tiếp (như đầu câu b đã nói) \(\Rightarrow\widehat{AOK}+\widehat{ACK}=180^0\)
\(\Rightarrow\widehat{AIK}=\widehat{ACK}\) (4)
Lại có tứ giác ACDH nội tiếp (D và H cùng nhìn AC dưới 1 góc vuông)
\(\Rightarrow\widehat{ACK}+\widehat{AHD}=180^0\) mà \(\widehat{AHD}+\widehat{MHD}=180^0\Rightarrow\widehat{ACK}=\widehat{MDH}\) (5)
(4);(5) \(\Rightarrow\widehat{AIK}=\widehat{MHD}\Rightarrow DH||IK\) (2 góc so le trong bằng nhau)
\(\Rightarrow\dfrac{DM}{KM}=\dfrac{HM}{IM}\) (định lý Talet)
Mặt khác \(CH||IB\) (cùng vuông góc AB)
\(\Rightarrow\dfrac{CM}{BM}=\dfrac{HM}{IM}\)
\(\Rightarrow\dfrac{DM}{KM}=\dfrac{CM}{BM}\Rightarrow DM.BM=KM.CM\)
Đúng 1
Bình luận (0)
tưởng anh Thịnh lên c3 rồi chứ
Đúng 0
Bình luận (2)
giúp câu c, ko cần làm câu a,b

a: Xét ΔABD vuông tại D và ΔCBA vuông tại A có
góc B chung
=>ΔABD đồng dạng vơi ΔCBA
=>BA^2=BD*BC
b: Xét ΔBIC vuông tại I và ΔBDH vuông tại D có
góc DBH chung
=>ΔBIC đồng dạng với ΔBDH
=>BD*BC=BI*BH
c: BA=BK
BD*BC=BI*BH
mà BA^2=BD*BC
nên BK^2=BI*BH
=>ΔBKH vuông tại K
Đúng 0
Bình luận (0)
một xe cần cẩu nâng một vật lên, Vậy xe cần cẩu đã tác dụng vào vật một lực:
Câu A: lực kéo
Câu B : lực đẩy
Câu C : lục nâng
Câu D : lực hút
Chọn câu nào ạ
Cần bạn giải câu c với câu d hộ ạ

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
b: BC=12cm nên BH=CH=6cm
=>AH=8cm
c: Xét ΔABC có
H là trung điểm của BC
HE//AC
DO đó: E là trung điểm của AB
Ta có: ΔAHB vuông tại H
mà HE là trung tuyến
nên HE=AE
hay ΔAEH cân tại E
Đúng 2
Bình luận (0)
 Chỉ cần ra kết quả câu c,d,ê cần gấp
Chỉ cần ra kết quả câu c,d,ê cần gấp
a 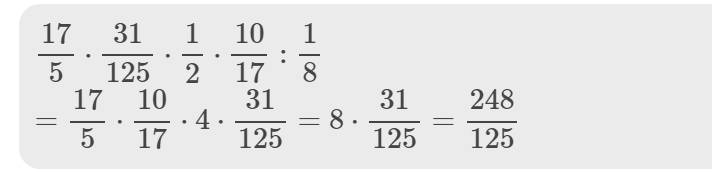
b: 
c: =6/7(8/13+1-3/13)
=6/7*18/13
=108/91
d: =9/25*-53/3-9/25*22/3
=9/25(-53/3-22/3)
=9/25*(-25)=-9
e: =2/5(-10/9+1/9)
=-2/5
Đúng 1
Bình luận (0)





